A Method of Computing/Determining the Arrhenius/non-Arrhenius Kinetic Parameters of the Exothermic Decomposition Reaction of Energetic Materials from Data of DSC Curves at Different Heating Rate
1 引言
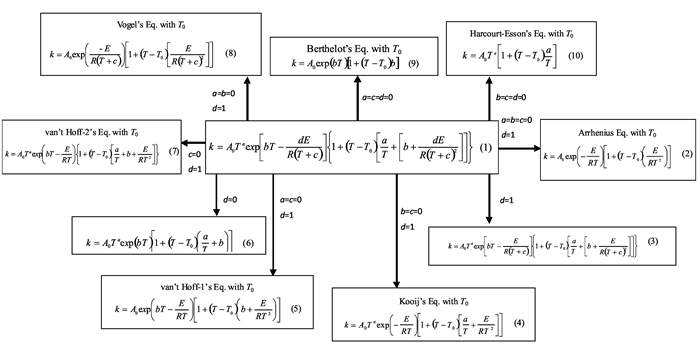
图 1为含DSC曲线起始温度(T0)的反应速率常数(k)的通式及其派生式。图中，式(1)为描述k-T关系的通式，式(2)~式(10)为式(1)在特定条件下的派生式。式(2)中的A0和E分别为Arrhenius动力学参数—表观指前因子和表观活化能。式(3)~式(10)中A0、a、b、E为非Arrhenius动力学参数。本工作报道了这些非Arrhenius动力学参数的计算方法，计算了四水双(3-(5-硝基-1, 2, 4-三唑))钠[Na2(BNT)(H2O)4]放热分解反应的Arrhenius/非Arrhenius动力学参数，用所得的非Arrhenius动力学参数计算了热爆炸临界温度(Tb)，并与用Arrhenius动力学参数所得的Tb值作比较，借此验证本工作所得非Arrhenius动力学参数的有效性和可靠性。
2 计算非Arrhenius动力学参数的理论和方法
由含初始温度(T0)的非等温动力学方程的微分式[1]
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right] \cdot \left\{ {1 + \left( {T - {T_0}} \right)\left[ {\frac{a}{T} + \left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right]} \right]} \right\}f\left( \alpha \right)
$
|
(11) |
分离变量，并分别在T0到T，和0到α间积分，得积分式
|
$
\begin{array}{l}
G\left( \alpha \right) = \int_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \frac{{{A_0}}}{\beta }\int_{{T_0}}^T {{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]\left\{ {1 + \left( {T - {T_0}} \right)\left[ {\frac{a}{T} + \left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right]} \right]} \right\}{\rm{d}}T} \\
\;\;\;\;\;\;\;\;\; = \frac{{{A_0}}}{\beta }\int_{{T_0}}^T {{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]\left\{ {1 + a + T\left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right] - \frac{T}{{{T^0}}}a - {T^0}\left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right]} \right\}{\rm{d}}T} \\
\;\;\;\;\;\;\;\;\; = \int_{{T_0}}^T {\left\{ {\left( {1 + a} \right)\frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right] + T\left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right]\frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]} \right\}{\rm{d}}T} \\
\;\;\;\;\;\;\;\;\;\;\;\; - T\int_{{T_0}}^T {\left\{ {\frac{{{A_0}}}{\beta }{T^{a - 1}}\exp \left[ {b - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]a + \frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]\left[ {b + \frac{{dE}}{{R{{\left( {T + c} \right)}^2}}}} \right]} \right\}} {\rm{d}}T\\
\;\;\;\;\;\;\;\;\; = \int_{{T_0}}^T {{\rm{d}}\left\{ {\frac{{{A_0}}}{\beta }{T^{a + 1}}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]} \right\}} - {T_0}\int_{{T_0}}^T {{\rm{d}}\left\{ {\frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]} \right\}} \\
\;\;\;\;\;\;\;\;\; = \frac{{{A_0}}}{\beta }{T^{a + 1}}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]\left| {_{{T_0}}^T} \right. - {T_0}\frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right]\left| {_{{T_0}}^T} \right.\\
\;\;\;\;\;\;\;\;\; = \frac{{{A_0}}}{\beta }{T^{a + 1}}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right] - \frac{{{A_0}}}{\beta }{T^{a + 1}}\exp \left[ {b{T_0} - \frac{{dE}}{{R\left( {{T_0} + c} \right)}}} \right] - {T_0}\frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right] +\\\;\;\;\;\;\;\;\; \frac{{{A_0}}}{\beta }{T^{a + 1}}\exp \left[ {b{T_0} - \frac{{dE}}{{R\left( {{T_0} + c} \right)}}} \right]\\
\;\;\;\;\;\;\;\;\; = \frac{{{A_0}}}{\beta }{T^a}\exp \left[ {bT - \frac{{dE}}{{R\left( {T + c} \right)}}} \right] \cdot \left( {T - {T_0}} \right)
\end{array}
$
|
(12) |
由式(12)两边取对数、重排，定义T为Te or p，α为αe or p，得对数形式的积分表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - \frac{{dE}}{{R\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c} \right)}}
$
|
(13) |
据此，知
(1) a=b=c=0，d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] - \frac{E}{{R{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}
$
|
(14) |
计算A0和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0和E值。
(2) d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - \frac{E}{{R\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c} \right)}}
$
|
(15) |
计算A0、a、b和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + b\sum\limits_{i = 1}^x {\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + a\sum\limits_{i = 1}^x {{{\left( {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} +\\ b\sum\limits_{i = 1}^x {\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} +\\ a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} + b\sum\limits_{i = 1}^x {{{\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} -\\ \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} + \\a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} + b\sum\limits_{i = 1}^x {\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)}^2}}
$
|
代原始数据c=0.15 K、βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得c=0.15 K时的A0、a、b和E值。
(3) b=c=0，d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - \frac{E}{{R{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}
$
|
(16) |
计算A0、a和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} +\\ a\sum\limits_{i = 1}^x {{{\left( {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} =\\ \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} +\\ a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} -\\ \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0、a和E值。
(4) a=c=0，d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - \frac{E}{{R{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}
$
|
(17) |
计算A0、b和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + b\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} + b\sum\limits_{i = 1}^x {{{\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} - \left( {\frac{E}{R}} \right)x
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} + bx - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0、b和E值。
(5) d=0时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}
$
|
(18) |
计算A0、a和b的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + b\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + a\sum\limits_{i = 1}^x {{{\left( {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} + b\sum\limits_{i = 1}^x {\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} + b\sum\limits_{i = 1}^x {{{\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0、a和b值。
(6) c=0，d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - \frac{E}{{R\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}
$
|
(19) |
计算A0、a、b和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + b\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + a\sum\limits_{i = 1}^x {{{\left( {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} +\\ b\sum\limits_{i = 1}^x {\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} =\\ \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} +\\ a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} +\\ b\sum\limits_{i = 1}^x {{{\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}} - \left( {\frac{E}{R}} \right)x
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} =\\ \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} + \\a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)} +\\ bx - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0、a、b和E值。
(7) a=b=0，d=1时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] - \frac{E}{{R\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c} \right)}}
$
|
(20) |
计算A0和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)} - \left( {\frac{E}{R}} \right)\sum\limits_{i = 1}^x {{{\left( {\frac{1}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} + c}}} \right)}^2}}
$
|
代原始数据c=0.15 K、βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得c=0.15 K时的A0和E值。
(8) a=c=d=0时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + b{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}
$
|
(21) |
计算A0和E的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} - b\sum\limits_{i = 1}^x {\ln \left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)} - b\sum\limits_{i = 1}^x {\ln {{\left( {{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0和E值。
(9) b=c=d=0时的表达式
|
$
\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right) = \ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right] + a\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}
$
|
(22) |
计算A0和a的超定方程组：
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]} + a\sum\limits_{i = 1}^x {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}
$
|
|
$
\sum\limits_{i = 1}^x {\ln \left( {\frac{{{\beta _i}}}{{{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}} - {T_{0i}}}}} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} = \sum\limits_{i = 1}^x {\ln \left[ {\frac{{{A_0}}}{{G\left( {{\alpha _{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}}} \right]\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} + a\sum\limits_{i = 1}^x {{{\left( {\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}} \right)}^2}}
$
|
代原始数据βi、T0i、Tei or pi、αei or pi，i=1, 2, …, L，入超定方程组，得A0和a值。
3 不考虑起始温度T0的非等温放热分解反应的动力学行为
3.1 计算用特征/原始数据
计算用Na2(BNT)(H2O)4放热分解反应的DSC曲线、特征数据(βi、T0i、Tei、αei、Tpi、αpi)和原始数据表：
|
$
\left. \begin{array}{l}
{\beta _1}:{T_{11}},{T_{12}}, \cdots ,{T_{1{k_1}}}\\
\;\;\;\;\;\;{\alpha _{11}},{\alpha _{12}}, \cdots ,{\alpha _{1{k_1}}}\\
{\beta _2}:{T_{21}},{T_{22}}, \cdots ,{T_{2{k_2}}}\\
\;\;\;\;\;\;{\alpha _{21}},{\alpha _{22}}, \cdots ,{\alpha _{2{k_2}}}\\
\;\;\;\;\;\; \cdots \cdots \cdots \cdots \\
{\beta _L}:{T_{L1}},{T_{L2}}, \cdots ,{T_{L{k_L}}}\\
\;\;\;\;\;\;{\alpha _{L1}},{\alpha _{L2}}, \cdots ,{\alpha _{L{k_L}}}
\end{array} \right\}
$
|
(23) |
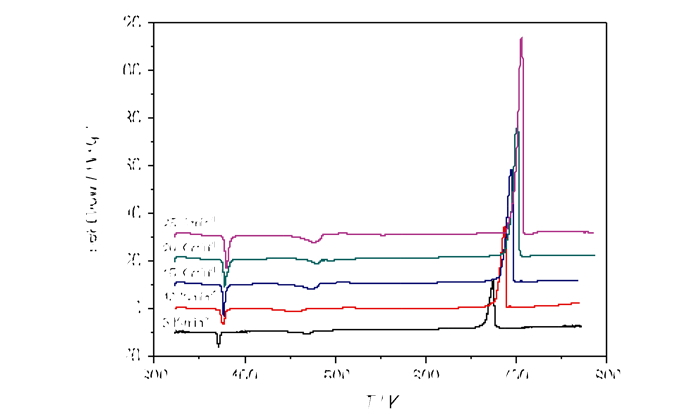
如图 2、表 1和表 2所示。其中, T0、Te和Tp分别为初始分解温度、onset温度和峰顶温度，αe和αp分别是Te和Tp时的反应转化率。Tij和αij(i=1，2, …，L；j=1，2，…，ki)是互相对应的反应温度和反应转化率，而ki是升温速率βi时的实验中所取的数据点个数。
表 1(Tab. 1)
表 1 非等温DSC测得Na2(BNT)(H2O)4原始数据和Kissinger法、Ozawa法和方程(27)、(28)所得放热分解反应的动力学参数
Tab. 1 The original data of Na2(BNT)(H2O)4 determined by non-isothermal DSC and kinetic parameters of exothermic decomposition reaction obtained by Kissinger′s method, Ozawa′s method and Eqs. (27)[2] and (28)[3]
| β/K·min-1 |
initial data |
|
calculated values of kinetic parameters1) |
|
Eq.(27) |
|
Eq.(28) |
|
T0/K |
Te/K |
αe
|
Tp/K |
αp
|
|
T00/K |
Te0/K |
Tp0/K |
Kissinger′s method |
|
Ozawa′s method |
|
be02)
|
re0
|
bp02)
|
rp0
|
|
ae03)
|
re0
|
ap03)
|
rp0
|
| EK/kJ·mol-1 |
lg(Ak/s-1) |
rK
|
|
EOp/kJ·mol-1 |
rOp
|
EOe/kJ·mol-1 |
rOe
|
| 5 |
649.96 |
666.87 |
0.1232 |
674.00 |
0.6880 |
|
643.26 |
652.10 |
656.79 |
191.31 |
12.46 |
0.9993 |
|
192.82 |
0.9993 |
189.97 |
0.9968 |
|
0.0516 |
0.9958 |
0.0513 |
0.9990 |
|
34.21 |
0.9963 |
34.39 |
0.9992 |
| 10 |
660.76 |
678.72 |
0.1028 |
686.86 |
0.6980 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 15 |
677.29 |
685.51 |
0.0678 |
694.23 |
0.6652 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 20 |
684.13 |
693.30 |
0.1127 |
701.22 |
0.6791 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 25 |
687.17 |
697.90 |
0.1434 |
705.13 |
0.6050 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note: 1) E : apparent activation energy; A : pre-exponential constant; Subscript K, data obtained by Kissinger′s method[4]; Subscript O: data obtained by Ozawa′s method [5].
2) The value of be0 or p0 is from lnβi
vs. Tei or Tpi relation in Eq. (27). 3) The value of ae0 or p0 is from lnβi
vs. Tei or Tpi relation in Eq. (28).
|
|
表 1 非等温DSC测得Na2(BNT)(H2O)4原始数据和Kissinger法、Ozawa法和方程(27)、(28)所得放热分解反应的动力学参数
Tab.1 The original data of Na2(BNT)(H2O)4 determined by non-isothermal DSC and kinetic parameters of exothermic decomposition reaction obtained by Kissinger′s method, Ozawa′s method and Eqs. (27)[2] and (28)[3] |
表 2(Tab. 2)
表 2 不同升温速率(β)下由DSC数据和非线性等转化率法(NL-INT)[6]得到的Na2(BNT)(H2O)4放热分解反应的表观活化能
Tab. 2 Data of Na2(BNT)(H2O)4 determined by DSC at different heating rates (β) and apparent activation energies (Ea) of thermal decomposition obtained by an integral isoconversional non-linear (NL-INT) method[6]
| data point |
initial data |
ENL-INT-SY3/kJ·mol-1 |
Min |
|
α
|
T5/K |
T10/K |
T15/K |
T20/K |
T25/K |
| 0 |
0.000 |
649.96 |
660.76 |
677.29 |
684.13 |
687.17 |
|
|
| 1 |
0.025 |
660.28 |
672.41 |
683.57 |
689.55 |
692.42 |
170.48 |
0.0064 |
| 2 |
0.050 |
662.97 |
675.47 |
684.82 |
690.98 |
694.16 |
180.88 |
0.0228 |
| 3 |
0.075 |
664.70 |
677.47 |
685.76 |
692.05 |
695.46 |
186.60 |
0.0089 |
| 4 |
0.100 |
665.96 |
678.62 |
686.55 |
692.91 |
696.49 |
189.58 |
0.0064 |
| 5 |
0.125 |
666.93 |
679.44 |
687.21 |
693.65 |
697.35 |
191.22 |
0.0064 |
| 6 |
0.150 |
667.67 |
680.12 |
687.80 |
694.29 |
698.08 |
191.99 |
0.0067 |
| 7 |
0.175 |
668.24 |
680.70 |
688.32 |
694.86 |
698.73 |
192.04 |
0.0070 |
| 8 |
0.200 |
668.73 |
681.21 |
688.80 |
695.37 |
699.31 |
191.94 |
0.0072 |
| 9 |
0.225 |
669.16 |
681.68 |
689.24 |
695.84 |
699.84 |
191.73 |
0.0073 |
| 10 |
0.250 |
669.54 |
682.10 |
689.64 |
696.28 |
700.33 |
191.39 |
0.0076 |
| 11 |
0.275 |
669.90 |
682.50 |
690.02 |
696.69 |
700.78 |
191.14 |
0.0077 |
| 12 |
0.300 |
670.23 |
682.86 |
690.38 |
697.07 |
701.21 |
190.81 |
0.0079 |
| 13 |
0.325 |
670.55 |
683.21 |
690.72 |
697.43 |
701.61 |
190.60 |
0.0081 |
| 14 |
0.350 |
670.85 |
683.53 |
691.05 |
697.77 |
701.99 |
190.35 |
0.0081 |
| 15 |
0.375 |
671.14 |
683.83 |
691.36 |
698.09 |
702.35 |
190.15 |
0.0083 |
| 16 |
0.400 |
671.42 |
684.12 |
691.66 |
698.41 |
702.69 |
189.95 |
0.0086 |
| 17 |
0.425 |
671.69 |
684.40 |
691.94 |
698.71 |
703.03 |
189.75 |
0.0089 |
| 18 |
0.450 |
671.94 |
684.66 |
692.21 |
699.00 |
703.35 |
189.50 |
0.0092 |
| 19 |
0.475 |
672.19 |
684.92 |
692.48 |
699.27 |
703.66 |
189.35 |
0.0093 |
| 20 |
0.500 |
672.43 |
685.17 |
692.73 |
699.54 |
703.96 |
189.17 |
0.0097 |
| 21 |
0.525 |
672.66 |
685.40 |
692.98 |
699.80 |
704.25 |
188.96 |
0.0099 |
| 22 |
0.550 |
672.89 |
685.63 |
693.22 |
700.04 |
704.54 |
188.82 |
0.0102 |
| 23 |
0.575 |
673.10 |
685.85 |
693.45 |
700.28 |
704.81 |
188.61 |
0.0104 |
| 24 |
0.600 |
673.31 |
686.07 |
693.68 |
700.52 |
705.08 |
188.42 |
0.0107 |
| 25 |
0.625 |
673.51 |
686.28 |
693.89 |
700.74 |
705.33 |
188.28 |
0.0110 |
| 26 |
0.650 |
673.71 |
686.48 |
694.11 |
700.96 |
705.58 |
188.13 |
0.0111 |
| 27 |
0.675 |
673.90 |
686.68 |
694.31 |
701.18 |
705.81 |
188.00 |
0.0114 |
| 28 |
0.700 |
674.09 |
686.87 |
694.51 |
701.40 |
706.04 |
187.86 |
0.0118 |
| 29 |
0.725 |
674.27 |
687.06 |
694.70 |
701.60 |
706.25 |
187.80 |
0.0119 |
| 30 |
0.750 |
674.45 |
687.25 |
694.89 |
701.81 |
706.46 |
187.71 |
0.0121 |
| 31 |
0.775 |
674.62 |
687.42 |
695.08 |
702.00 |
706.66 |
187.62 |
0.0121 |
| 32 |
0.800 |
674.79 |
687.59 |
695.25 |
702.19 |
706.85 |
187.58 |
0.0124 |
| 33 |
0.825 |
674.96 |
687.76 |
695.42 |
702.37 |
707.04 |
187.57 |
0.0127 |
| 34 |
0.850 |
675.12 |
687.91 |
695.58 |
702.55 |
707.21 |
187.54 |
0.0130 |
| 35 |
0.875 |
675.26 |
688.06 |
695.73 |
702.72 |
707.37 |
187.47 |
0.0131 |
| 36 |
0.900 |
675.40 |
688.20 |
695.86 |
702.88 |
707.51 |
187.50 |
0.0135 |
| 37 |
0.925 |
675.57 |
688.34 |
695.99 |
703.04 |
707.63 |
187.78 |
0.0140 |
| 38 |
0.950 |
675.81 |
688.46 |
696.10 |
703.18 |
707.71 |
188.67 |
0.0154 |
| 39 |
0.975 |
676.31 |
688.59 |
696.20 |
703.31 |
707.75 |
191.34 |
0.0201 |
| 40 |
1.000 |
682.74 |
689.34 |
696.77 |
703.63 |
708.29 |
230.92 |
0.2800 |
|
表 2 不同升温速率(β)下由DSC数据和非线性等转化率法(NL-INT)[6]得到的Na2(BNT)(H2O)4放热分解反应的表观活化能
Tab.2 Data of Na2(BNT)(H2O)4 determined by DSC at different heating rates (β) and apparent activation energies (Ea) of thermal decomposition obtained by an integral isoconversional non-linear (NL-INT) method[6] |
3.2 用特征点数据计算动力学参数(EK or O、AK、ae0 or p0和be0 or p0)
代表 1中的特征数据：βi、T0i、Tei、Tpi(i=1, 2, …, 5)，入方程(24)，得表 1中的T00、Te0和Tp0值，入Kissinger方程(25)、Ozawa方程(26)和方程(27)、(28)，得表 1中的EK or O、AK、ae0 or p0和be0 or p0值。
|
$
{T_{0\;{\rm{or}}\;{\rm{e}}\;{\rm{or}}\;{\rm{p}}}} = {T_{00\;{\rm{or}}\;{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}} + b{\beta _i} + c\beta _i^2 + d\beta _i^3\;\;\;\;i = 1,2, \cdots ,L
$
|
(24) |
|
$
\ln \left( {\frac{{{\beta _i}}}{{T_{{\rm{p}}i}^2}}} \right) = \ln \frac{{{A_{\rm{K}}}R}}{{{E_{\rm{K}}}}} - \frac{{{E_{\rm{K}}}}}{R}\frac{1}{{{T_{{\rm{p}}i}}}}
$
|
(25) |
|
$
\lg {\beta _i} = \lg \left[ {\frac{{{A_{\rm{K}}}{E_{{\rm{Oe}}\;{\rm{or}}\;{\rm{Op}}}}}}{{RG\left( \alpha \right)}}} \right] - 2.315 - 0.4567\frac{{{E_{{\rm{Oe}}\;{\rm{or}}\;{\rm{Op}}}}}}{{R{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}}}
$
|
(26) |
|
$
\lg {\beta _i} = \ln \left[ {\frac{{{A_0}}}{{{b_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}G\left( \alpha \right)}}} \right] + {b_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}{T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}
$
|
(27) |
|
$
\lg {\beta _i} = \ln \left[ {\frac{{{A_0}}}{{\left( {{a_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}} + 1} \right)G\left( \alpha \right)}}} \right] + \left( {{a_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}} + 1} \right)\ln {T_{{\rm{e}}i\;{\rm{or}}\;{\rm{p}}i}}
$
|
(28) |
3.3 用非线性等转化率积分法[6]估算动力学参数ENL-INT-SY3
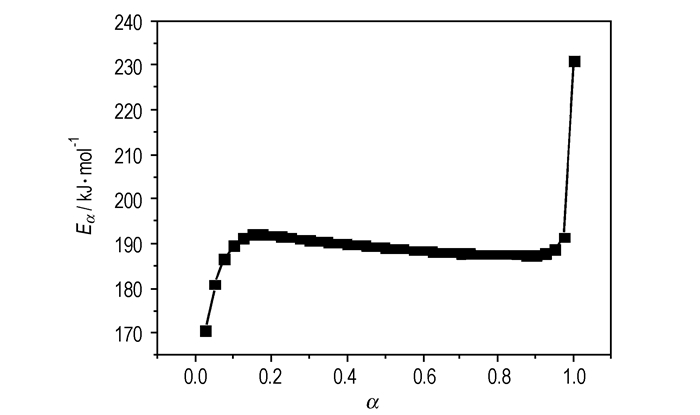
代表 2中同一α处的原始数据βi、Tα,i(i=1, 2, …, 5)，入方程(29)和(30)，得表 2中满足该方程最小(Min)值的ENL-INT-SY3值。用ENL-INT-SY3, i、αi(i=1, 2, …, 40)数据构筑ENL-INT-SY3-α关系曲线，结果如图 3所示。该曲线表明，α在0.100~0.975范围内，ENL-INT-SY3=(189.34±0.51) kJ·mol-1，E随α变化甚微，意味Na2(cis-BNT)(H2O)4放热分解过程可用某一机理函数描述。
|
$
{\Omega _{1{\bf{I}}}}\left( {{E_\alpha }} \right) = \min \left| {\sum\limits_{i = 1}^n {\sum\limits_{j \ne i}^n {\frac{{{\beta _{\rm{j}}} \cdot I\left( {{E_\alpha },{T_{\alpha ,i}}} \right)}}{{{\beta _{\rm{j}}} \cdot I\left( {{E_\alpha },{T_{\alpha ,j}}} \right)}}} } - n\left( {n - 1} \right)} \right|
$
|
(29) |
式中，I (Eα, Tα)积分取Senum-Yang三级近似式(30)计算：
|
$
{{I}_{\text{SY3}}}\left( E,T \right)=\left[ T{{\text{e}}^{-u}}\left( \frac{{{u}^{2}}+10u+18}{{{u}^{3}}+12{{u}^{2}}+36u+24} \right) \right]
$
|
(30) |
式中，u=E/RT。
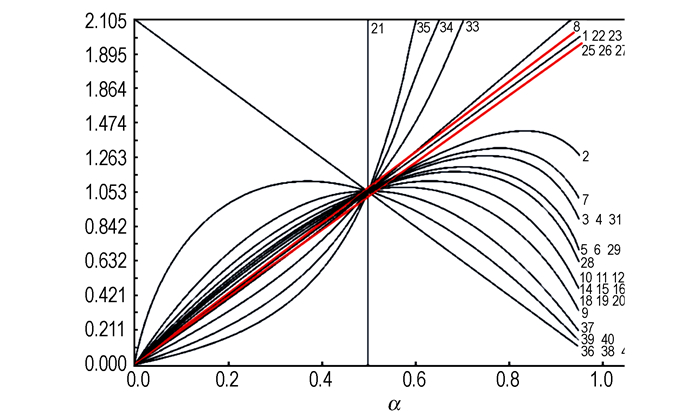
3.4 用“y(α)-α”标准曲线推断最可几f(α)[7]
将人为数据：αi, y(αi), i=1, 2, …, j和α=0.5，y(0.5)代入关系式$y(\alpha) = \frac{{f\left(\alpha \right) \cdot G(\alpha)}}{{f\left({0.5} \right) \cdot G(0.5)}}$作如图 4所示的“y(α)-α”关系曲线，视该曲线为标准曲线。
将表 2中原始数据：αi, Ti, $\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = \frac{\beta }{{60}} \cdot \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)$, i=1, 2, …j和α=0.5，T0.5，${\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{0.5}}$代入关系式$y(\alpha) = {\left({\frac{T}{{{T_{0.5}}}}} \right)^2}\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right){\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)_{0.5}}$作“y(α)-α”关系曲线，视该曲线为实验曲线。
α=0.100~0.975范围内的实验数据点全部落在图 4所示两条红线间，表明，可能的机理函数有7个，分别为：第1、22、23、24、25、26和27号函数，它们有逻辑形式通式：G(α)=αn[n=2(1D)、1/4、1/3、1/2、1、3/2、2]，因此，要明确指出哪个函数就是所求的f(α)是相当困难的。
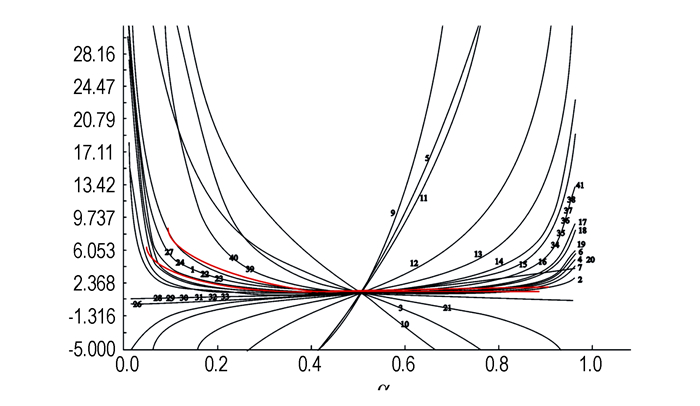
3.5 用“w(α)-α”标准曲线推断最可几f(α)[7]
将人为数据：αi, w(αi), i=1, 2, …, j和α=0.5，w(0.5)代入关系式$w\left( \alpha \right) = \frac{{f\left( {0.5} \right) \cdot f'\left( \alpha \right)}}{{f'\left( {0.5} \right) \cdot f\left( \alpha \right)}}$作如图 5所示的"w(α)-α"关系曲线，视该曲线为标准曲线。
将表 2中原始数据：αi, Ti, ${\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)_i}$, i=1, 2, …j和α=0.5，T0.5，${\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)_{0.5}}$代入关系式$w(\alpha) = \frac{{\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)}}{{{{\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)}_{0.5}}}}{\left({\frac{{{T_{0.5}}}}{T}} \right)^2}$作"w(α)-α"关系曲线，视该曲线为实验曲线。
α=0.100~0.975范围内的实验数据点全部落在图 5所示两条红线间，表明，可能的机理函数有5个，分别为：第1、22、23、24和27号函数，它们有逻辑形式通式：G(α)=αn[n=2(1D)、1/4、1/3、1/2、2]，因此，要明确指出哪个函数就是所求的f(α)也是相当困难的。
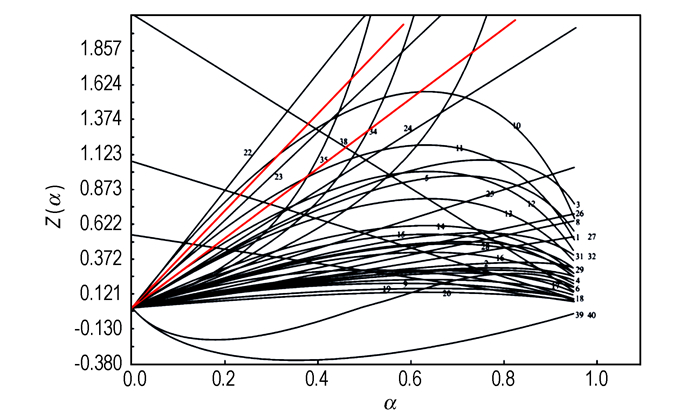
3.6 用“Z(α)-α”标准曲线推断最可几f(α)[7]
将人为数据：αi, Z(αi)，i=1, 2, …, j代入关系式Z(α)＝f(α)G(α)作图 6所示的“Z(α)-α”关系曲线，视该曲线为标准曲线。
将表 2中原始数据：β, αi, Ti, ${\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}{t}}} = \frac{\beta }{{60}} \cdot \frac{{{\rm{d}}\alpha }}{{{\rm{d}}{T}}}} \right)_i}$, i=1, 2, …j和Ozawa法所得的E值，代入关系式
|
$
Z\left( \alpha \right) = \frac{{{\rm{ \mathit{ π} }}\left( u \right)\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right)T}}{\beta }
$
|
式中, ${\rm{ \mathit{ π} }}(u) = \frac{{{u^2} + 10u + 18}}{{{{\rm{u}}^3} + 12{{\rm{u}}^2} + 36u + 24}}, u = E/RT$。作“Z(α)-α”关系曲线，视该曲线为实验曲线。
α=0.100~0.975范围内的实验数据点全部落在图 6所示两条红线附近，推断第22、23、24号函数可能为最可几机理函数，至此，我们仍不能明确哪个函数是最概然的，此处仅提供了很可能是第22号、23号和24号函数中的一个这一信息。
3.7 用逻辑选择法推断最可几机理函数f(α)[8]
为推断反应的最可几机理函数f(α)，进行了代α=0.100~0.975范围内的数据：βi、Ti和αi(i=1, 2, …, 36)和文献[8]中41个积分形式机理函数，入Šatava-Šesták方程(方程式(31))
|
$
\log G\left( \alpha \right) = \log \frac{{{A_{\rm{s}}}{E_{\rm{s}}}}}{{R\beta }} - 2.315 - 0.4567\frac{{{E_{\rm{s}}}}}{{RT}}
$
|
(31) |
求E和A的计算，结果如表 3~表 5所示。
表 3(Tab. 3)
表 3 用Šatava-Šesták法分析表 1中5, 10 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab. 3 Analysis results of the thermal decomposition data at 5, 10 K·min-1of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method
|
β=5 K·min-1 |
|
β=10 K·min-1 |
Function
No. |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
|
Function
No. |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
| 22 |
202.11 |
13.28 |
0.9967 |
1.030 |
3.360 |
|
22 |
204.68 |
13.48 |
0.9980 |
0.6454 |
1.319 |
| 23 |
269.48 |
18.63 |
0.9967 |
1.830 |
5.974 | |
23 |
272.91 |
18.79 |
0.9980 |
1.147 |
2.346 |
| 3 |
487.97 |
36.06 |
0.996 |
0.644 |
0.2268 | |
3 |
493.20 |
36.04 |
0.9989 |
2.010 |
2.207 |
| 4 |
1951.9 |
154.2 |
0.996 |
10.31 |
3.629 | |
4 |
1972.8 |
153.3 |
0.9989 |
32.16 |
35.32 |
| 5 |
520.91 |
38.65 |
0.9987 |
2.761 |
3.649 | |
5 |
526.07 |
38.58 |
0.9971 |
5.985 |
17.16 |
| 10 |
297.58 |
20.96 |
0.9933 |
4.619 |
31.03 | |
10 |
299.99 |
21.00 |
0.9900 |
6.874 |
68.85 |
| 7 |
1903.2 |
149.9 |
0.9997 |
7.320 |
1.924 | |
7 |
1924.3 |
149.0 |
0.9934 |
18.29 |
12.01 |
| 8 |
1452.6 |
112.9 |
0.9945 |
89.27 |
487.4 | |
8 |
1471.5 |
112.5 |
0.9960 |
65.00 |
258.2 |
| 35 |
2330.2 |
23.54 |
0.9188 |
77.30 |
6274 | |
35 |
335.54 |
23.76 |
0.9231 |
73.40 |
5644.8 |
| 1 |
1616.9 |
127.4 |
0.9967 |
65.89 |
215.0 | |
1 |
1637.5 |
126.9 |
0.9980 |
41.30 |
84.44 |
| 11 |
396.77 |
28.93 |
0.9933 |
8.211 |
55.16 | |
11 |
399.99 |
28.88 |
0.9900 |
12.22 |
12.24 |
| 12 |
476.13 |
35.32 |
0.9933 |
11.82 |
79.43 | |
12 |
479.99 |
35.21 |
0.9900 |
17.60 |
17.63 |
| 13 |
595.16 |
44.94 |
0.9933 |
18.47 |
124.1 | |
13 |
599.99 |
44.72 |
0.9900 |
27.50 |
27.54 |
| 14 |
793.55 |
61.00 |
0.9933 |
32.84 |
220.6 | |
14 |
799.98 |
60.61 |
0.9900 |
48.88 |
48.96 |
| 15 |
892.74 |
65.04 |
0.9933 |
41.57 |
279.2 | |
15 |
899.98 |
68.57 |
0.9900 |
61.87 |
61.97 |
| 16 |
1190.3 |
93.19 |
0.9933 |
73.90 |
496.4 | |
16 |
1200.0 |
92.46 |
0.9900 |
1099 |
1102 |
| 17 |
1785.5 |
141.6 |
0.9933 |
166.3 |
111.7 | |
17 |
1800.0 |
140.3 |
0.9900 |
2475 |
2479 |
| 18 |
2380.6 |
190.0 |
0.9933 |
295.6 |
198.6 | |
18 |
2400.0 |
188.2 |
0.9900 |
4400 |
4407 |
| 19 |
3571.0 |
286.9 |
0.9933 |
665.1 |
446.8 | |
19 |
3600.0 |
284.2 |
0.9900 |
9899 |
9915 |
| 20 |
4761.3 |
383.9 |
0.9933 |
1182 |
794.3 | |
20 |
4800.0 |
380.1 |
0.9900 |
1760 |
17.63 |
| 21 |
- |
- |
- |
- |
- | |
21 |
- |
- |
- |
- |
- |
| 6 |
2083.6 |
154.7 |
0.9987 |
44.18 |
58.38 | |
6 |
2104.3 |
163.5 |
0.9971 |
95.76 |
27.45 |
| 2 |
1816.0 |
143.4 |
0.9994 |
14.93 |
8.792 | |
2 |
1837.2 |
142.7 |
0.9996 |
10.12 |
4.039 |
| 24 |
404.23 |
29.41 |
0.9967 |
4.118 |
13.44 | |
24 |
409.36 |
29.50 |
0.9980 |
2.581 |
5.278 |
| 25 |
808.45 |
61.97 |
0.9967 |
16.47 |
53.76 | |
25 |
818.73 |
61.86 |
0.9980 |
10.33 |
21.11 |
| 26 |
1212.7 |
94.65 |
0.9967 |
37.07 |
121.0 | |
26 |
1228.1 |
94.34 |
0.9980 |
23.23 |
47.50 |
| 27 |
1616.9 |
127.4 |
0.9967 |
65.89 |
215.0 | |
27 |
1637.5 |
126.9 |
0.9980 |
41.30 |
84.44 |
| 28 |
1076.8 |
83.30 |
0.9978 |
19.94 |
44.49 | |
28 |
1087.0 |
82.79 |
0.9958 |
37.49 |
157.4 |
| 29 |
1041.8 |
80.57 |
0.9987 |
11.04 |
14.59 | |
29 |
1052.1 |
80.12 |
0.9971 |
23.94 |
68.63 |
| 30 |
1041.8 |
81.04 |
0.9987 |
11.04 |
14.60 | |
30 |
1052.1 |
80.59 |
0.9971 |
23.94 |
68.63 |
| 31 |
975.94 |
75.36 |
0.9996 |
2.578 |
0.9072 | |
31 |
986.40 |
75.02 |
0.9989 |
8.040 |
8.830 |
| 32 |
975.94 |
75.66 |
0.9996 |
2.578 |
0.9072 | |
32 |
986.40 |
75.32 |
0.9989 |
8.040 |
8.830 |
| 33 |
576.45 |
43.31 |
0.9755 |
6.481 |
1585 | |
33 |
585.08 |
43.43 |
0.9789 |
55.95 |
1179 |
| 34 |
429.33 |
31.49 |
0.9474 |
8.077 |
4246 | |
34 |
436.16 |
31.68 |
0.9516 |
74.56 |
3610 |
| 9 |
2723.5 |
217.2 |
0.9834 |
968.8 |
16056 | |
9 |
3740.4 |
214.7 |
0.9783 |
1265 |
27.45 |
| 36 |
959.83 |
75.04 |
0.8463 |
1403 |
215706 | |
36 |
954.20 |
73.44 |
0.8318 |
1523 |
256313 |
| 37 |
1768.3 |
140.5 |
0.9557 |
1140 |
50524 | |
37 |
1772.9 |
138.5 |
0.9473 |
1349 |
71.08 |
| 38 |
479.92 |
35.91 |
0.8463 |
350.8 |
53926 | |
38 |
477.10 |
35.26 |
0.8318 |
380.9 |
64.08 |
| 39 |
- |
- |
- |
- |
- | |
39 |
- |
- |
- |
- |
- |
| 40 |
- |
- |
- |
- |
- | |
40 |
- |
- |
- |
- |
- |
| 41 |
191.7 |
153.61 |
0.8463 |
5612 |
862823 | |
41 |
1909.4 |
150.1 |
0.8318 |
6094 |
1025252 |
|
表 3 用Šatava-Šesták法分析表 1中5, 10 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab.3 Analysis results of the thermal decomposition data at 5, 10 K·min-1of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method |
表 4(Tab. 4)
表 4 用Šatava-Šesták法分析表 1中15, 20 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab. 4 Analysis results of the thermal decomposition data at 15, 20 K·min-1 of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method
|
β=15 K·min-1 |
|
β=20 K·min-1 |
Function
No. |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
|
Function
No. |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
| 22 |
209.24 |
13.82 |
0.9959 |
1.303 |
5.382 | |
22 |
220.74 |
13.14 |
0.9961 |
1.230 |
4.793 |
| 23 |
278.98 |
19.20 |
0.9959 |
2.316 |
9. 567 | |
23 |
267.65 |
18.24 |
0.9961 |
2.186 |
8.522 |
| 3 |
504.99 |
36.71 |
0.9984 |
2.871 |
4.503 | |
3 |
484.61 |
34.85 |
0.9990 |
1.942 |
2.060 |
| 10 |
307.63 |
21.51 |
0.9910 |
6.173 |
55.50 | |
4 |
1938.4 |
147.6 |
0.9990 |
31.07 |
32.96 |
| 5 |
538.92 |
39.30 |
0.9972 |
5.885 |
16.59 | |
5 |
517.24 |
37.32 |
0.9978 |
4.559 |
9.953 |
| 6 |
2155.7 |
165.9 |
0.9972 |
94.16 |
265.4 | |
10 |
295.34 |
20.45 |
0.9919 |
5.537 |
44.62 |
| 7 |
169.9 |
151.1 |
0.9987 |
37.38 |
50.19 | |
7 |
1890.3 |
143.5 |
0.9991 |
24.87 |
22.21 |
| 8 |
1503.2 |
113.9 |
0.9933 |
1094 |
732.8 | |
8 |
1442.2 |
168.1 |
0.9936 |
105.2 |
677.5 |
| 35 |
339.88 |
23.98 |
0.9128 |
82.80 |
7223 | |
35 |
326.25 |
22.79 |
0.9135 |
82.18 |
7111 |
| 1 |
1673.9 |
128.5 |
0.9959 |
83.37 |
344.4 | |
1 |
605.89 |
122.0 |
0.9961 |
78.69 |
306.8 |
| 11 |
410.17 |
29.50 |
0.9910 |
10.97 |
98.67 | |
11 |
393.79 |
28.04 |
0.9919 |
9.843 |
79.32 |
| 12 |
492.21 |
35.92 |
0.9910 |
15.80 |
142.1 | |
12 |
472.55 |
34.14 |
0.9919 |
14.17 |
114.2 |
| 13 |
615.26 |
45.57 |
0.9910 |
24.69 |
222.0 | |
13 |
590.68 |
43.31 |
0.9919 |
21.15 |
178.5 |
| 14 |
820.34 |
61.68 |
0.9910 |
43.90 |
39.47 | |
14 |
787.58 |
58.62 |
0.9919 |
29.37 |
317.3 |
| 15 |
922.89 |
69.75 |
0.9910 |
55.56 |
49.95 | |
15 |
886.02 |
66.29 |
0.9919 |
49.83 |
401.6 |
| 16 |
1230.5 |
93.99 |
0.9910 |
98.77 |
88.80 | |
16 |
1181.4 |
89.33 |
0.9919 |
88.58 |
713.9 |
| 17 |
1845.8 |
142.6 |
0.9910 |
222.2 |
1998 | |
17 |
1772.1 |
135.5 |
0.9919 |
199.3 |
1606 |
| 18 |
2461.0 |
191.1 |
0.9910 |
395.1 |
3552 | |
18 |
2362.7 |
181.7 |
0.9919 |
354.3 |
2855 |
| 19 |
3691.6 |
288.4 |
0.9910 |
889.0 |
7992 | |
19 |
3544.1 |
274.1 |
0.9919 |
797.3 |
6425 |
| 20 |
4922.1 |
385.7 |
0.9910 |
1580 |
1421 | |
20 |
4725.4 |
368.6 |
0.9919 |
1417 |
11422 |
| 21 |
- |
- |
- |
- |
- | |
21 |
- |
- |
- |
- |
- |
| 2 |
1880.0 |
144.6 |
0.9985 |
37.78 |
56.30 | |
6 |
2069.0 |
157.6 |
0.9978 |
72.95 |
159.3 |
| 4 |
2020.0 |
155.4 |
0.9984 |
45.93 |
72.06 | |
2 |
1803.8 |
137.3 |
0.9989 |
28.71 |
32.50 |
| 24 |
418.47 |
30.03 |
0.9959 |
5.211 |
21.53 | |
24 |
401.47 |
28.52 |
0.9961 |
4.918 |
19.17 |
| 25 |
836.94 |
62.75 |
0.9959 |
20.84 |
86.11 | |
25 |
802.94 |
59.58 |
0.9961 |
19.67 |
76.70 |
| 26 |
1255.4 |
95.60 |
0.9959 |
46.90 |
193.7 | |
26 |
1204.4 |
90.77 |
0.9961 |
44.26 |
172.6 |
| 27 |
1673.9 |
128.5 |
0.9959 |
83.37 |
344.4 | |
27 |
1605.9 |
122.0 |
0.9961 |
78.69 |
306.8 |
| 28 |
1113.9 |
84.13 |
0.9961 |
34.81 |
135.7 | |
28 |
1069.1 |
79.90 |
0.9968 |
28.52 |
91.05 |
| 29 |
1077.9 |
81.39 |
0.9972 |
23.54 |
66.35 | |
29 |
1034.5 |
77.30 |
0.9978 |
18.24 |
39.81 |
| 30 |
1077.9 |
81.87 |
0.9972 |
23.54 |
66.35 | |
30 |
1034.5 |
77.78 |
0.9978 |
18.24 |
39.81 |
| 31 |
1010.0 |
76.19 |
0.9984 |
11.48 |
18.01 | |
31 |
969.22 |
72.34 |
0.9989 |
7.767 |
8.240 |
| 32 |
1010.0 |
76.48 |
0.9984 |
11.48 |
18.01 | |
32 |
969.22 |
72.65 |
0.9989 |
7.767 |
8.240 |
| 33 |
598.13 |
43.96 |
0.9737 |
69.71 |
1835 | |
33 |
571.85 |
41.73 |
0.9738 |
69.38 |
1818 |
| 34 |
443.03 |
32.01 |
0.9436 |
86.55 |
4885 | |
34 |
425.09 |
30.40 |
0.9439 |
86.03 |
4825 |
| 9 |
2812.7 |
218.2 |
0.9802 |
1156 |
22.88 | |
9 |
2701.2 |
207.40 |
0.9814 |
1083 |
20091 |
| 36 |
985.48 |
75.24 |
0.8386 |
1467 |
23685 | |
36 |
948.42 |
71.72 |
0.8414 |
1444 |
228950 |
| 37 |
1822.4 |
141.0 |
0.9506 |
1268 |
62.65 | |
37 |
1751.4 |
134.2 |
0.9524 |
1222 |
58125 |
| 38 |
492.74 |
36.24 |
0.8386 |
366.8 |
59.21 | |
38 |
474.21 |
34.55 |
0.8414 |
360.9 |
57237 |
| 39 |
- |
- |
- |
- |
- | |
39 |
- |
- |
- |
- |
- |
| 40 |
- |
- |
- |
- |
- | |
40 |
- |
- |
- |
- |
- |
| 41 |
1971.0 |
153.6 |
0.8386 |
5869 |
947391 | |
41 |
1896.9 |
146.4 |
0.9414 |
5774 |
915798 |
|
表 4 用Šatava-Šesták法分析表 1中15, 20 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab.4 Analysis results of the thermal decomposition data at 15, 20 K·min-1 of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method |
表 5(Tab. 5)
表 5 用Šatava-Šesták法分析表 1中25 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab. 5 Analysis results of the thermal decomposition data at 20 K·min-1 of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method
|
β=25 K·min-1 |
| Function No. |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
| 22 |
184.80 |
11.93 |
0.9973 |
0.850 |
2.290 |
| 23 |
246.40 |
16.58 |
0.9973 |
1.511 |
4.071 |
| 3 |
445.13 |
31.68 |
0.9979 |
3.893 |
8.284 |
| 4 |
270.56 |
18.50 |
0.9983 |
8.052 |
94.56 |
| 5 |
474.69 |
33.88 |
0.9959 |
8.552 |
35.05 |
| 6 |
1898.8 |
143.4 |
0.9959 |
136.8 |
560.8 |
| 7 |
1736.9 |
130.7 |
0.9984 |
44.31 |
70.54 |
| 8 |
1328.4 |
98.66 |
0.9953 |
77.48 |
367.0 |
| 35 |
302.36 |
20.90 |
0.9207 |
75.58 |
5994 |
| 1 |
1478.4 |
111.4 |
0.9973 |
54.41 |
146.6 |
| 11 |
360.75 |
25.41 |
0.9883 |
14.32 |
168.1 |
| 12 |
430.90 |
30.95 |
0.9883 |
20.61 |
242.1 |
| 13 |
541.12 |
39.29 |
0.9883 |
32.21 |
378.2 |
| 14 |
721.49 |
53.22 |
0.9883 |
57.26 |
672.4 |
| 15 |
811.68 |
60.19 |
0.9883 |
72.47 |
65.10 |
| 16 |
1082.2 |
81.15 |
0.9883 |
128.8 |
1513 |
| 17 |
1623.4 |
123.1 |
0.9883 |
289.9 |
3404 |
| 18 |
2164.5 |
165.2 |
0.9883 |
515.4 |
6052 |
| 19 |
3246.7 |
249.3 |
0.9883 |
1160 |
13616 |
| 20 |
4329.0 |
333.5 |
0.9883 |
2061 |
24207 |
| 21 |
- |
- |
- |
- |
- |
| 4 |
1780.5 |
134.5 |
0.9979 |
62.28 |
132.5 |
| 2 |
1658.5 |
125.2 |
0.9988 |
30.27 |
36.14 |
| 20 |
369.60 |
25.97 |
0.9973 |
3.400 |
9.160 |
| 25 |
739.21 |
54.35 |
0.9973 |
13.60 |
36.64 |
| 26 |
1108.8 |
82.85 |
0.9973 |
30.60 |
82.44 |
| 27 |
1478.4 |
111.4 |
0.9973 |
54.41 |
146.6 |
| 28 |
980.75 |
72.61 |
0.9945 |
49.48 |
274.3 |
| 29 |
949.39 |
70.29 |
0.9959 |
34.21 |
140.2 |
| 30 |
949.39 |
70.76 |
0.9959 |
34.21 |
140.2 |
| 31 |
890.25 |
65.94 |
0.9979 |
15.57 |
33.14 |
| 32 |
890.25 |
66.14 |
0.9979 |
15.57 |
33.14 |
| 33 |
528.18 |
38.18 |
0.9782 |
57.96 |
1266 |
| 34 |
393.43 |
27.85 |
0.9501 |
76.80 |
3833 |
| 9 |
2470.1 |
188.2 |
0.9760 |
1396 |
33510 |
| 36 |
856.91 |
64.25 |
0.8268 |
1564 |
270984 |
| 37 |
1596.1 |
121.3 |
0.9440 |
1433 |
80241 |
| 38 |
428.46 |
20.89 |
0.8268 |
391.1 |
67746 |
| 39 |
- |
- |
- |
- |
- |
| 40 |
- |
- |
- |
- |
- |
| 41 |
1713.8 |
131.3 |
0.8268 |
6257 |
1083937 |
|
表 5 用Šatava-Šesták法分析表 1中25 K·min-1时Na2(BNT)(H2O)4热分解数据的结果
Tab.5 Analysis results of the thermal decomposition data at 20 K·min-1 of Na2(BNT)(H2O)4 in Table 1 by Šatava-Šesták method |
据此，发现41个机理函数中有40个机理函数计算的E值均在含能材料正常范围外，即使E值在正常范围内, 如表 5的23号函数, E=246.40 kJ·mol-1, 也远离ENL-INT-SY3=189.34 kJ·mol-1，属不合理，被排除。只有第22号函数计算的E和A值在含能材料的E和A的正常范围(80~250 kJ·mol-1和107~1030 s-1)内，逻辑选择法所得的E =200.31 kJ·mol-1 (表 6)也接近ENL-INT-SY3=189.34 kJ·mol-1，因此，逻辑上较合理的最可几机理函数是第22号函数：G(α)=α1/4，f(α)=4α3/4。
表 6(Tab. 6)
表 6 用逻辑选择法分析表 3~表 5中Na2(BNT)(H2O)4热分解动力学数据的结果
Tab. 6 Analysis results of the thermal decomposition kinetic data of Na2(BNT)(H2O)4 in Tables 3-5 by logical choice method
|
β/K·min-1 |
E/kJ·mol-1 |
lg(A/s-1) |
r
|
Q·103 |
d·106 |
| 5 |
202.11 |
13.28 |
0.9967 |
1.030 |
3.360 |
| 10 |
204.68 |
13.48 |
0.9980 |
0.695 |
1.319 |
| 15 |
209.24 |
13.82 |
0.9959 |
1.303 |
5.382 |
| 20 |
200.74 |
13.14 |
0.9961 |
1.230 |
4.793 |
| 25 |
184.80 |
11.39 |
0.9973 |
0.850 |
2.290 |
| Mean |
200.31 |
13.13 |
|
|
|
|
表 6 用逻辑选择法分析表 3~表 5中Na2(BNT)(H2O)4热分解动力学数据的结果
Tab.6 Analysis results of the thermal decomposition kinetic data of Na2(BNT)(H2O)4 in Tables 3-5 by logical choice method |
据此，知在α从0.100~0.975的范围内，Na2(BNT)(H2O)4放热分解反应的速率方程为：$\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right) = {10^{13.73}}{\alpha ^{3/4}}{{\rm{e}}^{{\rm{ -24093/}}\mathit{T}}}$
3.8 ΔG≠、ΔH≠和ΔS≠值的估算
由热力学关系式(32)、(33)和(34)算得T=Tp0=656.79 K，E=Ea=191.31 kJ·mol-1，A=Aa=1012.46时，Na2(BNT)(H2O)4放热分解反应的活化热力学学参数为：活化自由能ΔG≠=199.81 kJ·mol-1，活化焓ΔH≠=185.85 kJ·mol-1，活化熵ΔS≠=-21.26 J·(K·mol)-1。
|
$
\Delta {G^ \ne } = E - RT\ln \left( {\frac{{Ah}}{{{k_{\rm{B}}}T}}} \right)
$
|
(32) |
|
$
\Delta {H^ \ne } = E - R{T_{{\rm{p0}}}}
$
|
(33) |
|
$
\Delta {S^ \ne } = \frac{{\Delta {H^ \ne } - \Delta {G^ \ne }}}{{{T_{{\rm{p0}}}}}}
$
|
(34) |
式中，kB为Boltzman常数，1.3807×10-23 J·K-1；h为plank常数，6.626×10-34 J·s-1。
负ΔS≠值，正ΔH≠和ΔG≠值, 表明Na2(BNT)(H2O)4有较好的对热抵抗能力。
3.9 动力学补偿效应
lnA与E呈线性关系的现象，谓之动力学补偿效应。其数学表达式为：
式中, a和b为补偿参数，a的单位为mol·kJ-1。
代表 6中E和A值，入方程(35)，得Na2(BNT)(H2O)4放热分解反应的动力学补偿效应方程
|
$
\ln A = 0.1790E - 5.5953
$
|
(36) |
该方程表明，A对E变化效应得到部分补偿。通过方程(36)，可从已知ENL-INT-SY3=189.34 kJ·mol-1，预测A=1012.92 s-1，从而知，Na2(BNT)(H2O)4放热分解反应速率方程：$\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right) = {10^{13.52}}{\alpha ^{3/4}}{{\rm{e}}^{{\rm{ -22774/}}\mathit{T}}}$
3.10 CnB反应动力学参数的估算
代表 2中α=0.100到αP的数据：β, αi, Ti，${\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = \frac{\beta }{{60}} \cdot \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}}} \right)_i}$, i=1, 2, …j, 入自催化n级反应(CnB)速率方程：
|
$
\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = A{{\rm{e}}^{ - E/RT}}{\left( {1 - \alpha } \right)^n}\left( {1 + {K_{{\rm{cat}}}}\alpha } \right)
$
|
(37) |
得表 7中的动力学参数。
表 7(Tab. 7)
表 7 Na2(BNT)(H2O)4自催化n级反应(CnB)的动力学参数
Tab. 7 The kinetic parameters of the n-order autocatalytic reaction (CnB) for the thermal decomposition of Na2(BNT)(H2O)4
|
β/K·min-1 |
E/kJ·mol-1 |
lg(A/s-1) |
n
|
Kcat
|
| 5.0 |
169.84 |
10.37 |
0.299 |
12.30 |
| 10.0 |
170.55 |
10.48 |
0.251 |
11.43 |
| 15.0 |
169.66 |
10.52 |
0.366 |
9.97 |
| 20.0 |
169.62 |
10.50 |
0.305 |
9.37 |
| 25.0 |
169.72 |
10.38 |
0.495 |
13.95 |
| Mean |
169.88 |
10.45 |
0.34 |
11.40 |
|
表 7 Na2(BNT)(H2O)4自催化n级反应(CnB)的动力学参数
Tab.7 The kinetic parameters of the n-order autocatalytic reaction (CnB) for the thermal decomposition of Na2(BNT)(H2O)4 |
据此，知Na2(BNT)(H2O)4的CnB速率方程为：$\left({\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}}} \right) = {10^{10.45}}{{\rm{e}}^{{\rm{ -20433/}}\mathit{T}}}{\left({1 -\alpha } \right)^{0.34}}\left({1 + 11.4\alpha } \right)$
4 考虑起始温度(T0)的Na2(BNT)(H2O)4的非等温放热分解反应的动力学行为
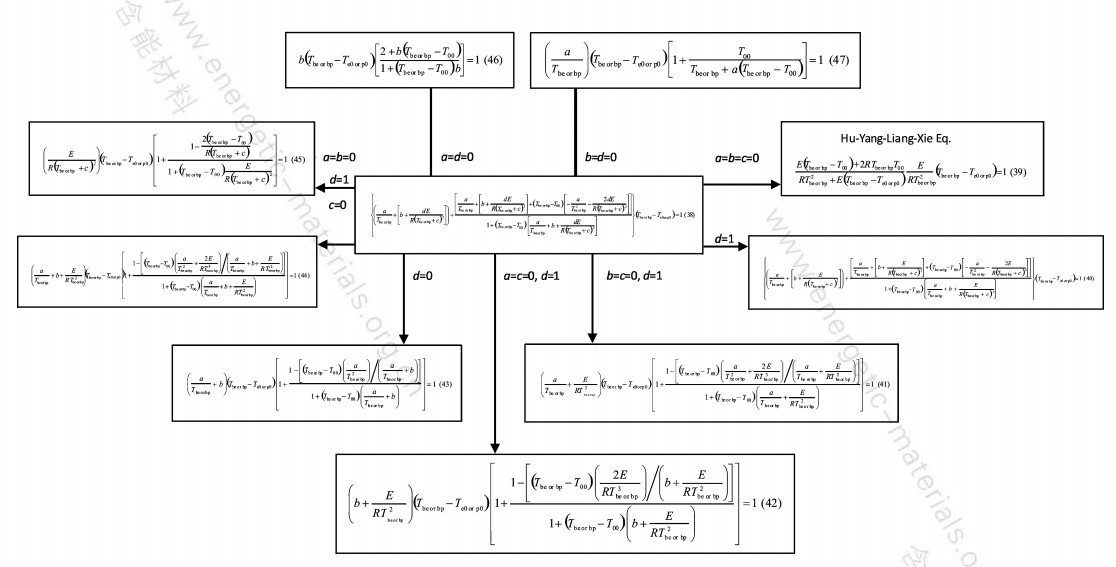
代表 1中的特征数据(βi、T0i、Tei or pi、αei or pi，i=1, 2, …, 5)，入方程(14)~(22)，得表 8中相应方程的非Arrhenius动力学参数：lg(A0/s-1)、a、b、E值，代这些a、b、E值，入图 7中方程(39)~(47)[9]，得表 9中的热爆炸临界温度值。用方程(39)得到的Tbe、Tbp值与方程(40)~(47)所得的Tbe、Tbp值相吻合，佐证本工作提出的“从不同升温速率下的DSC曲线数据计算/确定含能材料放热分解反应Arrhenius/非Arrhenius动力学参数的方法”有效、可靠。
表 8(Tab. 8)
表 8 用超定系统法得到的Na2(BNT)(H2O)4放热分解反应的非Arrhenius动力学参数1)
Tab. 8 The non-Arrhenius kinetic parameters of the exothermic decomposition reaction of Na2(BNT)(H2O)4 obtained by an overdetermined system method1)
| kinetic parameters |
Eq.(14) |
Eq.(15) |
Eq.(16) |
Eq.(17) |
Eq.(18) |
Eq.(19) |
Eq.(20) |
Eq.(21) |
Eq.(22) |
| values of kinetic parameters obtained by data (βi,
T0 i,
Te i,
αe i,
i=1, 2, …, L) in Table 1 and c=0 |
| lg(A0/s-1) |
19.66 |
|
18.03 |
17.88 |
-245.95 |
16.25 |
|
-23.75 |
-143.7 |
|
a
|
|
|
0.5 |
|
0.5 |
0.5 |
|
|
49.98 |
|
b
|
|
|
|
0.003 |
0.0725 |
0.003 |
|
0.0732 |
|
|
E/kJ·mol-1 |
283.54 |
|
280.70 |
271.93 |
|
269.10 |
|
|
|
| values of kinetic parameters obtained by data (βi,
T0 i,
Tp i,
αp i,
i=1, 2, …, L) in Table 1 and c=0 |
| lg(A0/s-1) |
16.90 |
|
15.26 |
15.10 |
-22.28 |
13.46 |
|
-21.08 |
-126.2 |
|
a
|
|
|
0.5 |
|
0.5 |
0.5 |
|
|
43.72 |
|
b
|
|
|
|
0.003 |
0.0627 |
0.003 |
|
0.0634 |
|
|
E/kJ·mol-1 |
250.50 |
|
247.64 |
238.65 |
|
235.79 |
|
|
|
| values of kinetic parameters obtained by data (βi,
T0 i,
Tp i,
αp i,
i=1, 2, …, L) in Table 1 and c=0.15 |
| lg(A0/s-1) |
|
16.25 |
|
|
|
|
19.67 |
|
|
|
a
|
|
0.5 |
|
|
|
|
|
|
|
|
b
|
|
0.003 |
|
|
|
|
|
|
|
|
E/kJ·mol-1 |
|
269.21 |
|
|
|
|
283.66 |
|
|
| values of kinetic parameters obtained by data (βi,
T0 i,
Tp i,
αp i,
i=1, 2, …, L) in Table 1 and c=0.15 |
| lg(A0/s-1) |
|
13.47 |
|
|
|
|
16.90 |
|
|
|
a
|
|
0.5 |
|
|
|
|
|
|
|
|
b
|
|
0.003 |
|
|
|
|
|
|
|
|
E/kJ·mol-1 |
|
235.89 |
|
|
|
|
250.61 |
|
|
| Note: 1)
a=0.5 and b=0.003 in Table 5 are setting values[10].
|
|
表 8 用超定系统法得到的Na2(BNT)(H2O)4放热分解反应的非Arrhenius动力学参数1)
Tab.8 The non-Arrhenius kinetic parameters of the exothermic decomposition reaction of Na2(BNT)(H2O)4 obtained by an overdetermined system method1) |
表 9(Tab. 9)
表 9 用表 8和表 1中数据得到的Na2(BNT)(H2O)4的热爆炸临界温度
Tab. 9 The critical temperature of thermal explosion of Na2(BNT)(H2O)4 obtained by data in Tables 8 and Tables 1
|
Tbe or bp/K |
Eq. with T0 |
|
Eq. without T0 |
| Arrhenius |
|
non-Arrhenius |
|
Arrhenius |
|
non-Arrhenius |
| Eq.(39) |
|
Eq.(40) |
Eq.(41) |
Eq.(42) |
Eq.(43) |
Eq.(44) |
Eq.(45) |
Eq.(46) |
Eq.(47) |
|
Eq.(48) |
|
Eq.(49) |
Eq.(50) |
|
Tbe
|
661.31 |
|
661.32 |
661.30 |
661.32 |
661.68 |
661.32 |
661.30 |
661.68 |
661.49 |
|
671.86 |
|
671.49 |
671.74 |
|
Tbp
|
666.56 |
|
667.78 |
667.76 |
667.78 |
668.15 |
667.78 |
667.76 |
663.53 |
663.37 |
|
676.52 |
|
676.28 |
676.47 |
|
表 9 用表 8和表 1中数据得到的Na2(BNT)(H2O)4的热爆炸临界温度
Tab.9 The critical temperature of thermal explosion of Na2(BNT)(H2O)4 obtained by data in Tables 8 and Tables 1 |
为考察T0对Tb值的影响，进行了代表 1中的EOe or Op、Te0 or p0、be0 or p0和ae0 or p0值, 入方程(48)~(50)计算Tbe or bp值的计算，结果如表 6所示。由此可见，计算中，不考虑T0的Tbe or bp值要比考虑T0的Tbe or bp值高10 K左右。
|
$
{T_{{\rm{be}}0\;{\rm{or}}\;{\rm{bp0}}}} = \frac{{{E_{{\rm{Oe}}\;{\rm{or}}\;{\rm{Op}}}} - \sqrt {E_{{\rm{Oe}}\;{\rm{or}}\;{\rm{Op}}}^2 - 4{E_{{\rm{Oe}}\;{\rm{or}}\;{\rm{Op}}}}R{T_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}} }}{{2R}}
$
|
(48) |
|
$
{T_{{\rm{be}}0\;{\rm{or}}\;{\rm{bp0}}}} = {T_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}} + \frac{1}{{{b_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}}}
$
|
(49) |
|
$
{T_{{\rm{be}}0\;{\rm{or}}\;{\rm{bp0}}}} = \frac{{{a_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}}}{{{a_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}} - 1}}{T_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}
$
|
(50) |
5 结论
(1) 提出了从不同升温速率下的DSC曲线数据计算/确定含能材料放热分解反应Arrhenius/非Arrhenius动力学参数的方法。
(2) 在α从0.100到0.975的范围内，Na2(BNT)(H2O)4放热分解反应的速率遵循方程：$\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {10^{13.73}}{\alpha ^{3/4}}{{\rm{e}}^{ -24093/T}}$
(3) 在α从0.100到αp的范围内，Na2(BNT)(H2O)4的CnB速率方程为：$\frac{{{\rm{d}}\alpha }}{{{\rm{d}}t}} = {10^{10.45}}{{\rm{e}}^{ -20433/RT}}{\left({1 -\alpha } \right)^{0.34}}\left({1 + 11.4\alpha } \right)$
(4)ΔG≠=199.81 kJ·mol-1，ΔH≠=185.85 kJ·mol-1，ΔS≠=-21.26 J·(K·mol)-1，Tbe>660 K的事实，表明Na2(BNT)(H2O)4有较好的对热抵抗能力。
(5) 对于Na2(BNT)(H2O)4，不考虑T0的Tbe or bp值要比考虑T0的Tbe or bp值高10 K左右。
A method of computing/determining the Arrhenius/non-Arrhenius kinetic parameters of the exothermic decomposition reaction of energetic materials (EMs) was presented from initial temperature (Te), peak temperature (Tp), conversion degree (αei or pi) at Tei or pi and data (βi, Tα,i, i=1, 2, …, L) corresponding to isoconversation degree (αi) for DSC curves under different constant heating rate (β) conditions.
