巴西试验(Brazilian test), 也称间接拉伸试验或直径圆盘试验, 是通过平面压头在圆柱体侧面沿径向施加载荷, 在圆柱体内产生垂直于加载面的拉应力, 当载荷达到破坏力后, 试样发生破坏。此试验要求的试样制备简单、操作易行、所需材料少、实验费用低, 适合于快速测定不宜制备标准拉伸试样的场合。对尺寸较小的粒状发射药力学性能进行初步评价时, 巴西试验无疑是一种很好的选择。巴西试验起初用于测试岩石、水泥等脆性材料, 被国际岩石力学学会列为测试岩石抗拉强度的推荐方法之一[1-2]。Q Z Wang等人[3]采用带有平台的圆盘试样研究了岩石的抗拉强度和断裂韧性, 试验及数值计算表明, 圆盘试样的平台能够改善加载区域的应力集中, 确保裂纹从试样中心起裂。庞海燕等人[4-5]研究了不同加载方式巴西试验结果与直接拉伸试验结果的相关性。陈鹏万等人[6-7]采用巴西圆盘试验研究了生产工艺对PBX炸药力学性能的影响。
然而, 这些研究中采用的抗拉强度计算公式通常是基于试样受到集中载荷作用的力学模型, 而在发射药的巴西试验过程中, 由于发射药与平面压头的接触区域发生局部变形, 发射药实际受到的是分布载荷的作用。本研究针对发射药的受力特点, 在考虑分布载荷对试样中心应力影响的情况下, 应用弹性接触理论和弹性力学平面问题的相关理论分析其应力分布规律, 结合Griffith强度准则[8]得到了发射药抗拉强度的计算公式, 以期为研究发射药的力学性能提供一种更为准确的计算方法。
2 试验 2.1 材料与仪器试验材料:储存时间分别为39,44,47 a的11/7单基粒状发射药若干, 半径为2.80 mm, 长度为15.10, 6.00 mm。
压力测试仪(图 1), 自制, 该设备使用螺旋加载, 可实现发射药粒的静态压缩试验; 平面压板下方为NH-5K型推拉力计, 常州市蓝光电子有限公司, 用于记录发射药破碎时的载荷。

|
图 1 压力测试仪 Fig.1 Compression strength tester |
选取外形规整的发射药, 对储存时间为39, 44, 47 a, 长度为15.10, 6.00 mm的发射药试样分别进行巴西试验。测试前, 将发射药用红色印泥染红并在发射药和平面压头之间放置打印纸, 通过平面压头对发射药施加一对径向载荷, 当发射药产生初始裂纹时, 打印纸上红色印泥的宽度就是发射药与压头接触面的宽度, 即压痕宽度(见图 2), 推拉力计上的示数即为发射药的破坏载荷; 同时用摄像机记录裂纹的起裂及扩展过程。

|
图 2 发射药与压头接触面的宽度(压痕宽度) Fig.2 Interface width between propellant and indenter (width of indentation) |
图 3为发射药不同加载时期的照片, 由图 3可以看出, 初始裂纹发生在发射药端面的中心位置, 并沿着加载方向向外扩展, 最终发生对径劈裂, 图 3c发射药试样除了对径劈裂产生的两个大的碎块, 还出现了四个较小的条状碎块, 该条形碎块是由于发射药试样发生劈裂后, 平面压头继续挤压发射药试样以及加载区域的应力集中导致的。另外, 平面压头对圆柱状发射药的载荷在轴向上均匀分布, 发射药中轴向应力很小或为零, 可近似为平面应力状态。因此该试验满足中心起裂和平面应力条件, 即巴西试验适合于测量发射药的抗拉强度。

|
图 3 初始裂纹的发生与扩展 Fig.3 Photographs of crack initiation, crack extension and propellant splitting |
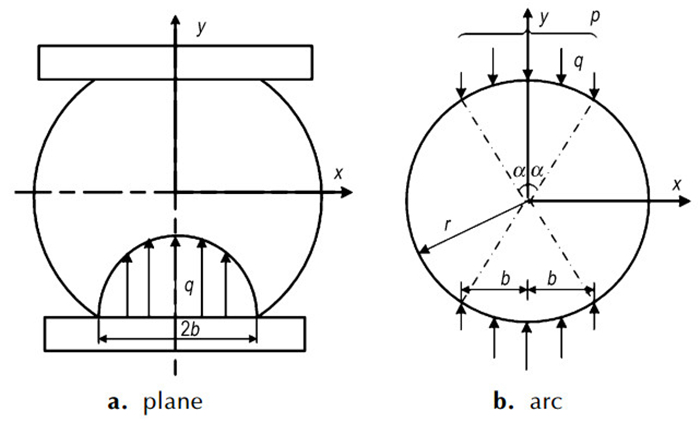
发射药为圆柱形, 试验初期平面压头与发射药之间为线接触, 随着载荷增加, 接触区域发生局部变形, 线接触变为面接触且接触面为矩形(见图 2红色印痕形状), 同时平面压头对发射药施加的载荷由线载荷变为分布载荷。这种情况可简化为刚性平面挤压圆柱体的弹性接触问题, 根据Hertz弹性接触理论[9], 在此类弹性接触问题中, 接触面(其宽度为2b)上任意一点的压力p与以接触面宽为直径作出的半圆的纵坐标成正比(如图 4a所示)。假设: 1、接触表面的摩擦阻力可忽略不计, 即接触面是理想光滑的; 2、接触面的尺寸与接触物体的曲率半径相比非常小。则接触面宽度的一半b、接触面上的最大压力p0、接触面上任意一点的压力p可分别表示为:
| $ {b^2} = \frac{{4rP}}{{\rm{ \mathsf{ π} }}}\left( {\frac{{1 - {\upsilon ^2}}}{E}} \right) $ | (1) |
| $ p_0^2 = \frac{P}{{{\rm{ \mathsf{ π} }}r}}{\left( {\frac{{1 - {\upsilon ^2}}}{E}} \right)^{ - 1}} $ | (2) |
| $ p = {p_0}\sqrt {1 - \frac{{{x^2}}}{{{b^2}}}} = \sqrt {\frac{P}{{{\rm{ \mathsf{ π} }}r}}{{\left( {\frac{{1 - {\upsilon ^2}}}{E}} \right)}^{ - 1}}\left( {1 - \frac{{{x^2}}}{{{b^2}}}} \right)} $ | (3) |
|
图 4 接触面压力分布示意图 Fig.4 Schematic diagram of the forces distribution in contact surface |
式中, E, 圆柱体的弹性模量, Pa; υ, 圆柱体的泊松比; r, 圆柱体半径, m; P, 圆柱体上单位长度的载荷, N/m; x, 以接触面宽为直径作出半圆的横坐标(见图 4a), m。
3.2 确定抗拉强度根据巴西试验结果, 试样的初始裂纹发生在试样的中心位置, 所以重点分析试样中心位置的应力状态。由圣维南原理[10]可知, 若用一组静力等效的力系来代替作用在物体局部边界上的面力, 则在力系作用区域附近的应力分布将显著改变, 但在远处所受的影响可以忽略不计。为了简化计算, 将图 4a中的接触平面用圆弧面替代(如图 4b所示), 当α较小时, 可用圆弧面代替接触平面, 忽略对试样中心位置应力状态的影响[10]。
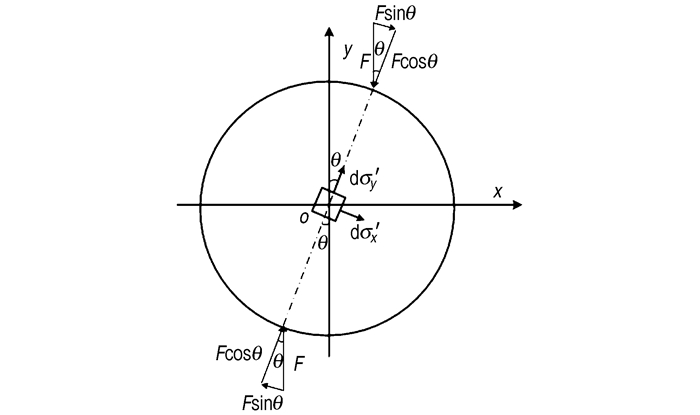
圆盘上的压力微元和应力微元示意图如图 5所示, 作用在圆弧上的压力微元F=qrdθ可分解为径向应力Fcosθ和切向应力Fsinθ, 而切向应力Fsinθ在宽度为2b的作用区域上形成自平衡, 根据圣维南原理[10], 切向应力对中心位置应力状态的影响可忽略不计, 因此, 试样中心位置的应力主要是由径向应力Fcosθ引起的[11]。依据弹性力学平面问题的相关理论[1, 12], 当圆盘受到一对沿圆盘直径方向, 大小相同, 方向相反的两个集中径向力Fcosθ作用时, 圆盘中心点的应力可表示为:
| $ {\rm{d}}{{\sigma '}_x} = \frac{{2F\cos \theta }}{{{\rm{ \mathsf{ π} }}D}} $ | (4) |
| $ {\rm{d}}{{\sigma '}_y} = - \frac{{6F\cos \theta }}{{{\rm{ \mathsf{ π} }}D}} $ | (5) |
|
图 5 圆盘上的压力微元和应力微元 Fig.5 Infinitesimal pressure and infinitesimal stress of disk |
式中, σx′, x′方向上的应力分量, Pa; σy′, y′方向上的应力分量, Pa; F, 压力微元, Pa·m; D, 圆盘直径, m。
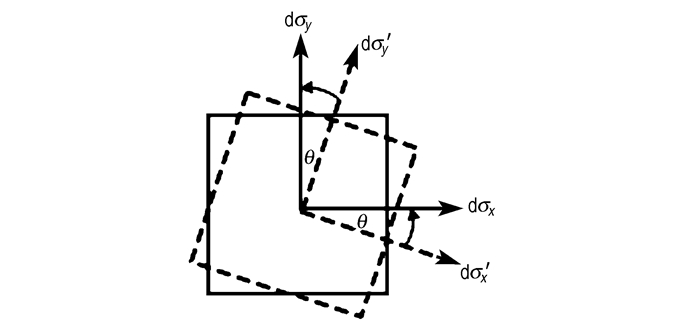
应力微元坐标转换示意图如图 6所示, 通过将坐标系Ox′y′旋转角度θ, 可得到圆盘中心位置应力微元在坐标系Oxy下的应力分量表达式[11]:
| $ {\rm{d}}{\sigma _x} = - \frac{{6F\cos \theta {{\sin }^2}\theta }}{{{\rm{ \mathsf{ π} }}D}} + \frac{{2F\cos \theta {{\cos }^2}\theta }}{{{\rm{ \mathsf{ π} }}D}} $ | (6) |
| $ {\rm{d}}{\sigma _y} = - \frac{{6F\cos \theta {{\cos }^2}\theta }}{{{\rm{ \mathsf{ π} }}D}} + \frac{{2F\cos \theta {{\sin }^2}\theta }}{{{\rm{ \mathsf{ π} }}D}} $ | (7) |
|
图 6 应力微元的坐标转换 Fig.6 Coordinates transformation of infinitesimal stress |
由图 4a和图 4b可知, x的取值范围为(-b, b), x/r=sinθ,
将式(3)分别代入式(6)和式(7)并积分得:
| $ \begin{array}{l} {\sigma _x} = \sqrt {\frac{{PE}}{{{{\rm{ \mathsf{ π} }}^3}r\left( {1 - {\upsilon ^2}} \right)}}} \int_{ - \alpha }^\alpha {\left( { - 3\cos \theta {{\sin }^2}\theta + \cos \theta {{\cos }^2}\theta } \right) \times } \\ \;\;\;\;\;\;\;\;\sqrt {1 - \frac{{{{\sin }^2}\theta }}{{{{\sin }^2}\alpha }}} {\rm{d}}\theta \end{array} $ | (8) |
| $ \begin{array}{l} {\sigma _y} = \sqrt {\frac{{PE}}{{{{\rm{ \mathsf{ π} }}^3}r\left( {1 - {\upsilon ^2}} \right)}}} \int_{ - \alpha }^\alpha {\left( { - 3\cos \theta {{\cos }^2}\theta + \cos \theta {{\sin }^2}\theta } \right) \times } \\ \;\;\;\;\;\;\;\;\sqrt {1 - \frac{{{{\sin }^2}\theta }}{{{{\sin }^2}\alpha }}} {\rm{d}}\theta \end{array} $ | (9) |
| $ \begin{array}{l} f\left( \alpha \right) = \int_{ - \alpha }^\alpha {\left( { - 3\cos \theta {{\sin }^2}\theta + \cos \theta {{\cos }^2}\theta } \right) \times } \\ \;\;\;\;\;\;\;\;\sqrt {1 - \frac{{{{\sin }^2}\theta }}{{{{\sin }^2}\alpha }}} {\rm{d}}\theta \end{array} $ | (10) |
| $ \begin{array}{l} \varphi \left( \alpha \right) = \int_{ - \alpha }^\alpha {\left( { - 3\cos \theta {{\cos }^2}\theta + \cos \theta {{\sin }^2}\theta } \right) \times } \\ \;\;\;\;\;\;\;\;\sqrt {1 - \frac{{{{\sin }^2}\theta }}{{{{\sin }^2}\alpha }}} {\rm{d}}\theta \end{array} $ | (11) |
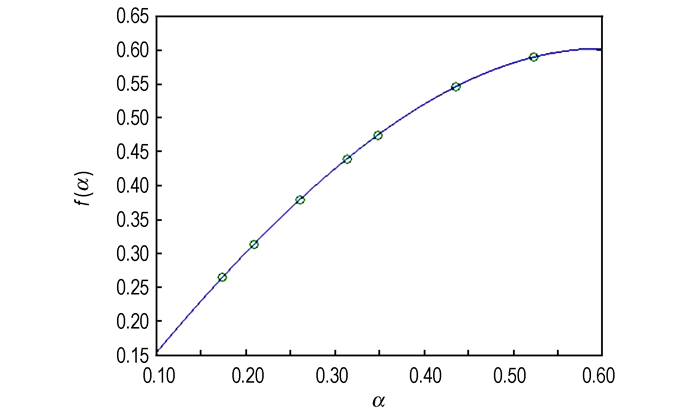
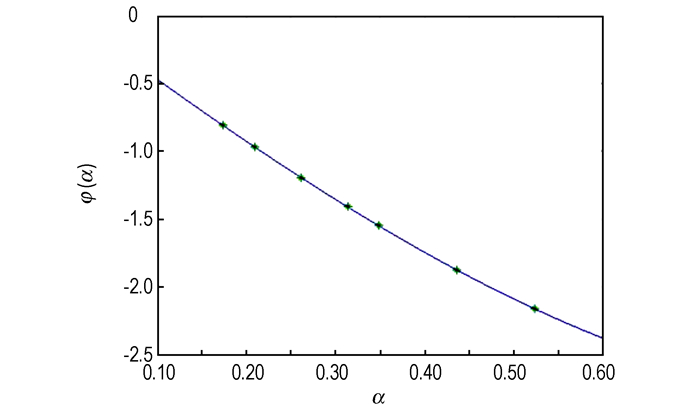
对于不同的试样, α有不同取值, 函数f(α)和φ(α)的值可通过数值积分得到, 如表 1所示。
| 表 1 f(α)和φ(α)的数值积分结果 Tab.1 Numerical integration results of f(α)and φ(α) |
为了简化计算, 依据表 1中的数据, 采用三次多项式对函数f(α)和φ(α)进行拟合可得:
| $ f\left( \alpha \right) = - 0.9339{\alpha ^3} - 0.5831{\alpha ^2} + 1.7068\alpha - 0.0107 $ | (12) |
| $ \varphi \left( \alpha \right) = 1.4283{\alpha ^3} + 0.6120{\alpha ^2} - 4.8561\alpha + 0.0115 $ | (13) |
拟合曲线如图 7和图 8所示, 由拟合曲线图可以看出, 当α取值在0.15~0.55之间时, 可用式(12)和式(13)分别代替式(10)和式(11)进行计算, 其误差可以忽略。
|
图 7 f(α)的拟合曲线图 Fig.7 The fitting curve of function f(α) |
|
图 8 φ(α)的拟合曲线图 Fig.8 The fitting curve of function φ(α) |
将式(12)和式(13)分别代入式(8)和式(9)得:
| $ {\sigma _x} = \sqrt {\frac{{PE}}{{{\pi ^3}{r^3}\left( {1 - {\upsilon ^2}} \right)}}} \left( { - 0.9339{\alpha ^3} - 0.5831{\alpha ^2} + 1.7068\alpha - 0.0107} \right) $ | (14) |
| $ {\sigma _y} = \sqrt {\frac{{PE}}{{{\pi ^3}{r^3}\left( {1 - {\upsilon ^2}} \right)}}} \left( {1.4283{\alpha ^3} + 0.6120{\alpha ^2} - 4.8561\alpha + 0.0115} \right) $ | (15) |
根据Griffith强度准则[8], 等效应力σG(Pa)根据最大主应力σ1和最小主应力σ3的组合情况计算得到, 即:当3σ1+σ3≥0, σG=σ1; 当3σ1+σ3<0,
| $ \begin{array}{l} {\sigma _t} = {\sigma _G} = - \frac{{{{\left( {{\sigma _x} - {\sigma _y}} \right)}^2}}}{{8\left( {{\sigma _x} + {\sigma _y}} \right)}} = \sqrt {\frac{{PE}}{{{\pi ^3}{r^3}\left( {1 - {\upsilon ^2}} \right)}}} \times \\ \frac{{{{\left( { - 2.3622{\alpha ^3} - 1.1951{\alpha ^2} + 6.5629\alpha - 0.0222} \right)}^2}}}{{ - 3.9552{\alpha ^3} - 0.2312{\alpha ^2} + 25.1944\alpha - 0.0064}} \end{array} $ | (16) |
由式(16)可以看出, 发射药的抗拉强度是由发射药破碎时单位长度的载荷P和接触面对应发射药圆心角的一半α决定的, 也即对于一定长度和直径的发射药, 抗拉强度由发射药破碎时的载荷和接触面宽度决定。
取发射药的泊松比为υ=0.3, 弹性模量为E=2.7 GPa, 将试验结果带入式(16)得到的抗拉强度计算结果如表 2所示。由表 2可以看出, 发射药长度对抗拉强度的影响不明显, 因此, 可用原尺寸的11/7单基粒状发射药(长度为15.10 mm)为试样进行巴西试验, 评价发射药的抗拉强度。当储存时间由39 a延长到47 a时, 发射药的抗拉强度由13.11 MPa变为12.58 MPa, 抗拉强度减小4%。
| 表 2 巴西试验的测试结果 Tab.2 The results of Brazilian test |
(1) 在发射药巴西试验中, 平面压头对圆柱状发射药的载荷在轴向上均匀分布, 可近似为平面应力状态; 另外, 初始裂纹发生在发射药端面的中心位置, 并沿着加载方向向外扩展, 最终发生对径劈裂, 因此该试验满足中心起裂和平面应力条件, 即巴西试验适合于测量发射药的抗拉强度。
(2) 文中针对巴西试验中发射药的受力特点, 应用Hertz弹性接触理论和弹性力学平面问题的相关理论分析其应力分布规律, 结合Griffith强度准则, 得到了发射药抗拉强度的计算公式:
| $ \begin{array}{l} {\sigma _t} = {\sigma _G} = - \frac{{{{\left( {{\sigma _x} - {\sigma _y}} \right)}^2}}}{{8\left( {{\sigma _x} + {\sigma _y}} \right)}} = \sqrt {\frac{{PE}}{{{\pi ^3}{r^3}\left( {1 - {\upsilon ^2}} \right)}}} \times \\ \;\;\;\;\;\;\;\;\;\frac{{{{\left( { - 2.3622{\alpha ^3} - 1.1951{\alpha ^2} + 6.5629\alpha - 0.0222} \right)}^2}}}{{ - 3.9552{\alpha ^3} - 0.2312{\alpha ^2} + 25.1944\alpha - 0.0064}} \end{array} $ |
(3) 发射药长度对抗拉强度的影响不明显, 因此, 可用原尺寸的11/7单基粒状发射药为试样进行巴西试验。发射药的抗拉强度主要由发射药破碎时的载荷和接触面宽度决定。当储存时间由39 a延长到47 a时, 发射药的抗拉强度由13.11 MPa变为12.58 MPa, 抗拉强度减小4%。
| [1] |
Jonsen P, Haggblad H A, Sommer K. Tensile strength and fracture energy of pressed metal powder by diametral compression test[J].
Powder Technology, 2007, 176: 148-155. DOI:10.1016/j.powtec.2007.02.030 |
| [2] |
Steven P Mates, Richard Rhorer, Stephen Banovic, et al. Tensile strength measurements of frangible bullets using the diametral compression test[J].
International Journal of Impact Engineering, 2008, 35: 511-520. DOI:10.1016/j.ijimpeng.2007.04.005 |
| [3] |
Wang Q Z, Jia X M, Kou S Q, et al. The flattened Brazilian disc specimen used for testing elastic modulus, tensile strength and fracture toughness of brittle rocks: analytical and numerical results[J].
International Journal of Rock Mechanics & Mining Sciences, 2004, 41: 245-253. |
| [4] |
庞海燕, 李明, 温茂萍, 等. 不同加载形式的PBX炸药巴西试验[J].
含能材料, 2012, 20(2): 205-209. PANG Hai-yan, LI Ming, WEN Mao-ping, et al. Different loading methods in Brazilian test for PBX[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2012, 20(2): 205-209. |
| [5] |
庞海燕, 李明, 温茂萍, 等. PBX巴西试验与直接拉伸试验的比较[J].
火炸药学报, 2011, 34(1): 42-44. PANG Hai-yan, LI Ming, WEN Mao-ping, et al. Comparison on the Brazilian test and tension test of the PBX[J]. Chinese Journal of Explosives and Propellant, 2011, 34(1): 42-44. |
| [6] |
CHEN Peng-wan, XIE Hui-min, HUANG Feng-lei, et al. Deformation and failure of polymer bonded explosives under diametric compression test[J].
Polymer Testing, 2006, 25: 333-341. DOI:10.1016/j.polymertesting.2005.12.006 |
| [7] |
陈鹏万, 黄风雷, 张瑜, 等. 用巴西实验评价炸药的力学性能[J].
兵工学报, 2001, 22(4): 533-537. CHEN Peng-wan, HUANG Feng-lei, ZHANG Yu, et al. Brazilian test and its application in the study of the mechanical properties of explosives[J]. Acta Armamentarii, 2001, 22(4): 533-537. |
| [8] |
王启智, 贾学明. 用平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度——第一部分:解析和数值结果[J].
岩石力学与工程学报, 2002, 21(9): 1285-1289. WANG Qi-zhi, JIA Xue-ming. Determination of elastic modulus, tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen——part I: analytical and numerical results[J]. Chinese Journal of Rock Mechanics and Engineeringt, 2002, 21(9): 1285-1289. |
| [9] |
Gladwell G M L, 经典弹性理论中的接触问题[M]. 范天佑译. 北京: 北京理工大学出版社, 1991: 327-355.
Gladwell G M L, Contact problem of classical elastic theory[M]. FAN Tian-you. Beijing: Beijing Institute of Technology Press, 1991: 327-355. |
| [10] |
吴家龙.
弹性力学[M]. 北京: 高等教育出版社, 2011: 244-256.
WU Jia-long. Elastic mechanics[M]. Beijing: Higher Education Press, 2011: 244-256. |
| [11] |
Wang Q Z, Jia X M, Kou S Q. The flattened Brazilian disc specimen used for testing elastic modulus, tensile strength and fracture toughness of brittle rocks: analytical and numerical results[J].
International Journal of Rock Mechanics & Mining Sciences, 2004(41): 245-253. |
| [12] |
宋华杰, 郝莹, 董海山, 等. 用直径圆盘试验评价小样品塑料粘结炸药拉伸性能的初步研究[J].
爆炸与冲击, 2001, 21(1): 35-40. SONG Hua-jie, HAO Ying, DONG Hai-shan, et al. A preliminary evaluation of tensile properties of small plastic bonded sample by diametric disc test[J]. Explosion and Shock Waves, 2001, 21(1): 35-40. |

The mechanical performance of granular propellant was studied by brazilian test taking the loading features into account. Theories of Hertz elastic contact and elastic mechanics plane stress were applied to analyze the stress distribution law, and the formula was obtained to calculate tensile strength for propellant from Griffith strength criteria.



