高聚物粘结炸药(PBX)是由单质炸药晶体与高聚物粘结剂组成的颗粒性材料, 是武器系统中常用的功能材料[1]。武器在使用、储运过程中往往经受不同的温度环境, 温度环境的改变可能会引起材料性能发生变化, 出现宏观裂纹, 从而影响其可靠性与安全性[2-3]。温度环境的改变同时会导致部件结构产生热应力, 热应力与应变及温度以复杂形式耦合在一起[4]。
许多学者对不同PBX炸药在不同温度下的力学性能进行了研究。Thompson[5]、Ellis[6]、罗景润[1]等分别试验获得了PBX-A(美国)、PBX-E(英国)、PBX-C(中国)三种HMX基的PBX炸药常温准静态单轴拉伸状态的力学性能, 包括其抗拉强度、抗拉应变及初始弹性模量, 如表 1所示。Drodge等[7]采用超声方法测量了268~303 K的HMX基PBX力学性能的变化, 给出了弹性模量、剪切模量、体积模量、泊松比等随温度变化规律的曲线, 其中弹性模量E(T)随着温度升高而大幅度降低[7], 泊松比ν(T)随着温度升高而升高(升幅不大, 一定程度上认为不变为v=0.4)。Williamson[8]和Thompson[5]分别研究了PBX-E、PBX-A的时温效应, 指出, 可以唯象地通过Williams Landel Ferry方程将应变率变化下的部分力学性能转化为热环境下的力学性能, 从而将PBX炸药的高应变率、蠕变规律研究等转化为准静态下的温度变化影响规律研究。韦兴文等[9]试验研究表明HMX基PBX炸药热膨胀系数在低于330 K的温度时可以认为不变, 约为5.34×10-5 K-1, 在330~350 K迅速增大到13.47×10-5 K-1, 随后减小到8.04×10-5 K-1。Gruau等[10]指出可以认为HMX基PBX单轴拉伸应力应变关系是线弹性的。
| 表 1 PBX-A、PBX-E、PBX-C材料的单轴拉伸力学性能 Tab.1 The mechanical properties of PBX-A, PBX-E and PBX-C materials in uniaxial tension |
PBX炸药适用强度理论研究是武器系统安全性与可靠性课题的重要内容, 是判断PBX炸药失效破坏的重要依据。唐维等[11-12]在研究PBX炸药的适用强度理论中比较分析了常用四种强度准则的适应性, 指出:从描述精度角度来看, Mohr-Coulomb准则最优, Twin-shear准则和Drucker-Prager准则次之, 现常用的最大正应力准则相对最差。Mohr-Coulomb准则能够较为准确描述颗粒性材料的拉伸强度与压缩强度不同特性, Drucker-Prager准则能够较为准确描述颗粒性材料的压力相关特性, 且便于实现数值计算。Mohr-Coulomb准则和Drucker-Prager准则都常用于颗粒性材料的失效分析中。王鹏飞等[13]在PBX炸药准静态压缩状态下的弹塑性变形的理论研究中采用了修正形状函数的线性Drucker-Prager准则, 该准则结合Mohr-Coulomb准则和Drucker-Prager准则的优点, 理论上描述精度更高, 且便于实现数值计算。唐维等[14]在PBX炸药单轴主要特征破坏参数研究中指出, 破坏应力受环境条件因素影响大, 不宜单独作为主特征破坏参数, 破坏应变受环境条件因素影响小, 可作为主特征破坏参数。颗粒性材料的破坏应变数值较小(单轴拉伸的破坏应变约为0.1%), 实验测量误差的随机性往往有可能掩盖了真实破坏应变值。因此理论分析实际应用中, 常采用破坏时组合各主应力之间的关系作为破坏特征。Mohr-Coulomb准则和Drucker-Prager准则的本质为各应力之间的协调关系, 并非将破坏应力单独作为破坏判断依据。
目前, 虽然许多学者开展了热环境下PBX力学性能实验研究, 但是目前从理论上来讨论热环境下PBX炸药及其炸药件的破坏机制并不多见, 具有明确物理意义的研究成果也较为缺乏。本研究针对HMX基PBX炸药厚壁球结构件(特殊构件)在热弹性环境下的失效破坏机理及状况开展研究(不考虑温度引起的化学变化)。采用包括最大拉应力准则、von-Mises准则、Mohr-Coulomb准则、Drucker-Prager准则等强度准则来分析球结构的承受温差能力与最先破坏点位置。根据特殊构件的失效破坏共性, 推广确定PBX普通构件的失效破坏特征及承受温差能力,分析比较PBX-A、PBX-B、PBX-C三种PBX的力学性能, 从而阐释选择低强度低弹性模量炸药的部分原因。
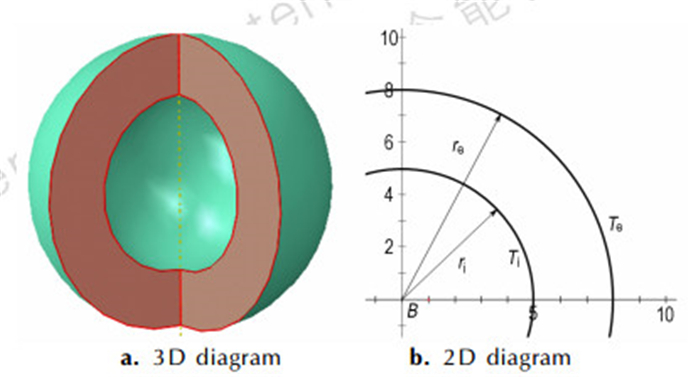
2 温度场方程PBX特殊结构厚壁球, 内半径为ri, 外半径为re, 如图 1所示。
|
图 1 PBX厚壁球结构示意图 Fig.1 Schematic diagrams of the PBX thick wall sphere structure |
为简化承受温差能力的计算, 假设温度场为定常温度场。球坐标下的温度场T=T(r, θ,
| $ \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}\frac{{\partial T}}{{\partial r}}} \right) = 0 $ | (1) |
方程通解为
| $ T = \frac{1}{r}\left( {\frac{{{r_{\rm{i}}}{r_{\rm{e}}}\left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{{r_{\rm{e}}} - {r_{\rm{i}}}}}} \right) - \left( {\frac{{{r_{\rm{i}}}{T_{\rm{i}}} - {r_{\rm{e}}}{T_{\rm{e}}}}}{{{r_{\rm{e}}} - {r_{\rm{i}}}}}} \right) $ | (2) |
在球坐标系中, 只有径向位移ur不为零, 并设ur=u, u为径向变形位移值; 周向正应力与切向正应力相等, 即
平衡方程[16]
| $ \frac{{{\rm{d}}{\sigma _r}}}{{{\rm{d}}r}} + 2\frac{{{\sigma _r} - {\sigma _\theta }}}{r} = 0 $ | (3) |
式中, σr为径向应力, MPa; σθ为周向应力, MPa。
几何方程[16]
| $ {\varepsilon _r} = \frac{{{\rm{d}}u}}{{{\rm{d}}r}},{\varepsilon _\theta } = \frac{u}{r} $ | (4) |
式中, εr为径向应变, εθ为周向应变。
应力应变关系[15]
| $ \begin{array}{l} {\varepsilon _r} = \frac{1}{E}\left( {{\sigma _r} - \nu \left( {{\sigma _\theta } + {\sigma _\varphi }} \right)} \right) + \alpha T = \frac{1}{E}\left( {{\sigma _r} - 2\nu {\sigma _\theta }} \right) + \alpha T\\ {\varepsilon _\theta } = \frac{1}{E}\left( {{\sigma _\theta } - \nu \left( {{\sigma _r} + {\sigma _\varphi }} \right)} \right) + \alpha T = \frac{1}{E}\left( {\left( {1 - \nu } \right){\sigma _\theta } - \nu {\sigma _r}} \right) + \alpha T \end{array} $ | (5) |
式中, α为温度系数; E为弹性模量, MPa; ν为泊松比。联立(3)(4)(5), 化简可得常微分方程[15]
| $ \frac{{{{\rm{d}}^2}u}}{{{\rm{d}}{r^2}}} + \frac{2}{r}\frac{{{\rm{d}}u}}{{{\rm{d}}r}} - \frac{{2u}}{{{r^2}}} = \frac{{\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\alpha \frac{{{\rm{d}}T}}{{{\rm{d}}r}} $ | (6) |
假设厚壁球内部无压力, 只考虑温度引起的热应力效应, 则其边界条件为: r=ri, σr=0; r=re, σr=0。式(6)可改写成:
| $ \frac{{\rm{d}}}{{\rm{d}}}\left( {\frac{1}{{{r^2}}}\frac{{\rm{d}}}{{{\rm{d}}r}}\left( {{r^2}u} \right)} \right) = \frac{{\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\alpha \frac{{{\rm{d}}T}}{{{\rm{d}}r}} $ | (7) |
对(7)式积分两次可得:
| $ u = \frac{{1 + \nu \alpha }}{{1 - \nu {r^2}}}\int_{{r_{\rm{i}}}}^r {T{r^2}{\rm{d}}r} + {C_1}r + \frac{{{C_2}}}{{{r^2}}} $ | (8) |
结合边界条件可解得[15]:
| $ {C_1} = \frac{{2\left( {1 - 2\nu } \right)}}{{1 - \nu }}\frac{\alpha }{{r_{\rm{e}}^3 - r_{\rm{i}}^3}}\int_{{r_{\rm{i}}}}^{{r_{\rm{e}}}} {T{r^2}{\rm{d}}r} ,{C_2} = \frac{{1 + \nu }}{{1 - \nu }}\frac{{\alpha r_{\rm{i}}^3}}{{r_{\rm{e}}^3 - r_{\rm{i}}^3}}\int_{{r_{\rm{i}}}}^{{r_{\rm{e}}}} {T{r^2}{\rm{d}}r} $ | (9) |
结合温度场方程, 可解得:
| $ {\sigma _r} = \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{1 - \nu }}\left( {\frac{{{r_{\rm{e}}}{r_{\rm{i}}}\left( {r - {r_{\rm{i}}}} \right)\left( {r - {r_{\rm{e}}}} \right)\left( {{r_{\rm{e}}}{r_{\rm{i}}} + r\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right)} \right)}}{{\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right) $ | (10) |
| $ {\sigma _\theta } = - \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{1 - \nu }}\left( {\frac{{{r_{\rm{e}}}{r_{\rm{i}}}\left( {r_{\rm{e}}^2r_{\rm{i}}^2 - 2{r^3}\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right) + {r^2}\left( {r_{\rm{e}}^2 + {r_{\rm{e}}}{r_{\rm{i}}} + r_{\rm{i}}^2} \right)} \right)}}{{2\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right) $ | (11) |
在内部无压力作用且仅受温度载荷(即温度差ΔT=Ti-Te)状况下, 球结构上的径向应力与周向应力都是由于温度差引起的, 即温度差的存在是结构产生热应力的根本原因, 因此可将承受温差能力作为热环境下失效分析的判据之一。分析式(10)(11)可以看出, 热应力的大小与弹性模量、温度载荷都成正比。在温度载荷相同、结构相同情况下, 弹性模量大的材料产生的热应力大, 弹性模量小的材料产生的热应力小; 若两种不同材料其所能承受的载荷极限相同, 则其中弹性模量偏小的能承受更大的温度载荷。可以判断出相同结构中PBX-C比PBX-A、PBX-E对温度载荷更敏感, 相同温度变化条件下产生更大的热应力。
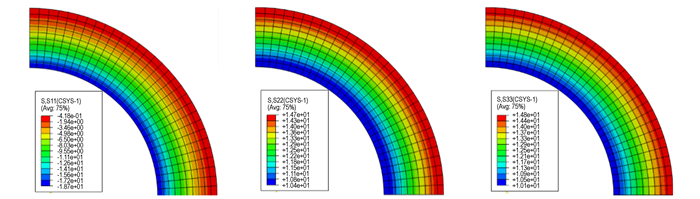
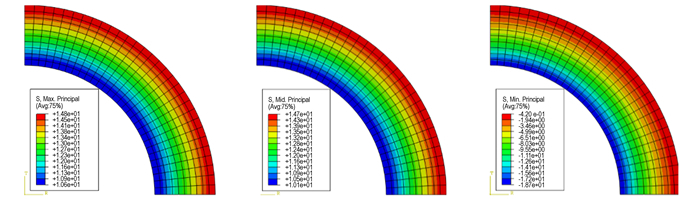
若内部温度比外部温度高, 即Ti-Te>0, 从(10)、(11)式可以判断出, 径向应力σr在球内外壁都为零, 且其在球(r≠ri, re)中产生的应力是压缩应力。球内壁和外壁仅受周向和切向热应力作用, 由σθ|re < 0可判断出其在内壁为典型的双轴压缩状态, 由σθ |re >0可知热应力在外壁为典型的双轴拉伸状态。则周向应力σθ是半径r的单调递增函数, 即在外壁r=re处取得最大值, 其应力分布示意图如图 2、图 3所示。
|
图 2 定常温度场下径向应力σr(s11)、周向应力σθ(s22)和切向应力 |
|
图 3 定常温度场下最大主应力、中间主应力和最小主应力分布示意图 Fig.3 Distribution diagrams of the maximumn principal stress, the middle principal stress and the minimumn principal stress in stesdy temperature field |
若内部温度比外部温度低, 即Ti-Te < 0, 从(10)、(11)式可以判断出, 径向应力σr在球内外壁都为零, 且其在球(r≠ri, re)中产生的应力是拉伸应力。球内壁和外壁仅受周向和切向热应力作用, 由σθ|re < 0可判断出其在外壁为典型的双轴压缩状态, 由σθ |ri >0可知热应力在内壁为典型的双轴拉伸状态。周向应力σθ是半径r的单调递减函数, 即在内壁r=ri处取得最大值。
5 多种强度准则分析现针对内部温度比外部温度高的状况在不同破坏准则下开展PBX厚壁球结构件承受温差能力及其首先屈服或破坏点位置的分析讨论。对于PBX炸药, 其拉伸强度远小于压缩强度, 因此对其拉伸强度和拉应力更加关注(根据前述热应力载荷的分布, 拉应力基本存在于外半壁)。
(1) 最大正应力准则
当最大正应力达到简单拉伸试验得出的材料抗拉强度时, 不论材料内其他正应力或剪应力如何, 材料都会发生破坏。对于PBX厚壁球结构, 则有:
| $ {\sigma _\theta }\left| {_{\max }} \right. = \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{1 - \nu }}\left( {\frac{{{r_{\rm{i}}}\left( {2{r_{\rm{i}}} + {r_{\rm{e}}}} \right)}}{{2\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} \right)}}} \right) = {\sigma _t} $ | (12) |
式中, σθ|max为材料最大周向应力, MPa; σt为PBX炸药的单轴拉伸强度, MPa。由σθ的单调递增性判断出, 仅有热应力的作用, 其最先破坏点在于外壁。最大正应力承受的最大温差载荷为:
| $ \begin{array}{l} \Delta T\left| {_{\max }} \right. = \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)\left| {_{\max }} \right. = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} \right)}}{{{r_{\rm{i}}}\left( {2{r_{\rm{i}}} + {r_{\rm{e}}}} \right)}}} \right)\\ \;\;\;\;\;\;\;\;\;\; = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {1 + \xi + {\xi ^2}} \right)}}{{\xi \left( {2\xi + 1} \right)}}} \right) \end{array} $ | (13) |
式中,
| $ \Delta T\left| {_{\max }} \right. = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\psi \left( \xi \right) $ | (14) |
(2) von-Mises准则
材料的破坏发生在其八面体应力τoct达到临界值σs。对于PBX厚壁球结构, 则有:
| $ \begin{array}{l} {\tau _{{\rm{oct}}}} = {\sigma _\theta } - {\sigma _t} = \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right){r_{\rm{e}}}{r_{\rm{i}}}}}{{1 - \nu }}\left( {\frac{{ - 3r_{\rm{e}}^2r_{\rm{i}}^2 + {r^2}\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{e}}}{r_{\rm{i}}}} \right)}}{{2\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right)\\ \;\;\;\;\; = {\sigma _s} \end{array} $ | (15) |
式中, σs可以取为σt。分析式(15), 可知等式左边可能在
| $ \begin{array}{l} \Delta T\left| {_{\max 1}} \right. = {\sigma _s}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{9\left( {{r_{\rm{e}}} - {r_{\rm{i}}}} \right)}}{{\sqrt {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} }}} \right)\\ \;\;\;\;\;\;\;\;\;\;\; = {\sigma _s}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{9\left( {1 - \xi } \right)}}{{\sqrt {1 + \xi + {\xi ^2}} }}} \right),\xi \le 0.422 \end{array} $ | (16) |
| $ \begin{array}{l} \Delta T\left| {_{\max 2}} \right. = {\sigma _s}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} \right)}}{{{r_{\rm{i}}}\left( {2{r_{\rm{i}}} + {r_{\rm{e}}}} \right)}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\; = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {1 + \xi + {\xi ^2}} \right)}}{{\xi \left( {2\xi + 1} \right)}}} \right),\xi > 0.422 \end{array} $ | (17) |
分析可知, 在ΔT|max2 ≥ΔT|max1, 且仅在ξ=0.422处取得等号, 而在
对于PBX厚壁球结构件, ξ≈1>0.422恒成立, 故可知其首先破坏点在外壁, 式(17)即是其能承受的最大温度载荷。式(17)可改写成:
| $ \Delta T\left| {_{\max }} \right. = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\psi \left( \xi \right) $ | (18) |
(3)Mohr-Coulomb准则
材料的破坏发生在材料中一点处任一平面上的剪应力与正应力成线性关系。PBX炸药有拉压不对称系数
| $ {\sigma _\theta } - \lambda {\sigma _r} = -\frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right){r_{\rm{e}}}{r_{\rm{i}}}}}{{1 - \nu }}\left( {\frac{{\left( {\lambda - 1} \right)\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right)}}{{r_{\rm{e}}^3 - r_{\rm{i}}^3}} + \frac{{\left( {r_{\rm{e}}^2 + {r_{\rm{e}}}{r_{\rm{i}}} + r_{\rm{i}}^2} \right)\left( {1 - 2\lambda } \right)}}{{2\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right)r}} + \frac{{r_{\rm{e}}^2r_{\rm{i}}^2\left( {1 + 2\lambda } \right)}}{{2\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right) = {\sigma _t} $ | (19) |
结合PBX炸药拉压不同的特性, 可知式(19)是半径r的单调递增函数, 其最大值在r=re处, 故其首先破坏点出现在外壁。其能承受的最大温度载荷为
| $ \Delta T\left| {_{\max }} \right. = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} \right)}}{{{r_{\rm{i}}}\left( {2{r_{\rm{i}}} + {r_{\rm{e}}}} \right)}}} \right) = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {1 + \xi + {\xi ^2}} \right)}}{{\xi \left( {2\xi + 1} \right)}}} \right) $ | (20) |
式(20)可改写成:
| $ \Delta T\left| {_{\max }} \right. = {\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\psi \left( \xi \right) $ | (21) |
(4) Drucker-Prager准则
Drucker-Prager准则是对von-Mises准则简单修正而形成的对Mohr-Coulomb面的光滑近似。对于PBX厚壁球结构, 则有:
| $ \begin{array}{l} {I_1} = \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{1 - \nu }}\left( {\frac{{{r_{\rm{e}}}{r_{\rm{i}}}\left( {3r\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right) - 2\left( {r_{\rm{e}}^2 + {r_{\rm{e}}}{r_{\rm{i}}} + r_{\rm{i}}^2} \right)} \right)}}{{\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right)r}}} \right)\sqrt {3{J_2}} \\ \;\;\; = \left| {\left( {{\sigma _{\rm{ \mathsf{ θ} }}} - {\sigma _{\rm{r}}}} \right)} \right|\\ \;\;\; = \left| {\frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right)}}{{1 - \nu }}\left( {\frac{{{r_{\rm{e}}}{r_{\rm{i}}}\left( { - 3r_{\rm{e}}^2r_{\rm{i}}^2 + {r^2}\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{e}}}{r_{\rm{i}}}} \right)} \right)}}{{2\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right)} \right| \end{array} $ | (22) |
| $ \begin{array}{l} f = {\alpha _1}{I_1} + \sqrt {3{J_2}} \\ \;\;\; = \frac{{E\alpha \left( {{T_{\rm{i}}} - {T_{\rm{e}}}} \right){r_{\rm{e}}}{r_{\rm{i}}}}}{{1 - \nu }}\left( {\frac{{ - 9r_{\rm{e}}^2r_{\rm{i}}^2 + \left( {3 - 4\tan \beta } \right){r^2}\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{e}}}{r_{\rm{i}}}} \right) + 6\tan \beta {r^3}\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right)}}{{6\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right){r^3}}}} \right)\\ \;\;\; = {K_1} \end{array} $ | (23) |
式中,
| $ \Delta T\left| {_{\max }} \right. = {K_1}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{1}{{\left( {\frac{{3 - 4\tan \beta }}{3}} \right)\frac{3}{2}\frac{{3\sqrt {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{e}}}{r_{\rm{i}}}} }}{{9\left( {{r_{\rm{e}}} - {r_{\rm{i}}}} \right)}} + \frac{{\tan \beta {r_{\rm{e}}}{r_{\rm{i}}}\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right)}}{{\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right)}}}}} \right) $ | (24) |
或
| $ \begin{array}{l} \Delta T\left| {_{\max }} \right. = {K_1}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{6\left( {r_{\rm{e}}^3 - r_{\rm{i}}^3} \right)}}{{ - 9r_{\rm{i}}^3 + \left( {3 - 4\tan \beta } \right)\left( {r_{\rm{e}}^2{r_{\rm{i}}} + r_{\rm{i}}^3 + {r_{\rm{e}}}r_{\rm{i}}^2} \right) + 6\tan \beta {r_{\rm{e}}}{r_{\rm{i}}}\left( {{r_{\rm{e}}} + {r_{\rm{i}}}} \right)}}} \right)\\ \;\;\;\;\;\;\;\;\;\; = \frac{{{K_1}}}{{\left( {1 + \frac{2}{3}\tan \beta } \right)}}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {r_{\rm{e}}^2 + r_{\rm{i}}^2 + {r_{\rm{i}}}{r_{\rm{e}}}} \right)}}{{{r_{\rm{i}}}\left( {2{r_{\rm{i}}} + {r_{\rm{e}}}} \right)}}} \right)\\ \;\;\;\;\;\;\;\;\;\; = \frac{{1 + \frac{1}{3}\tan \beta }}{{1 + \frac{2}{3}\tan \beta }}{\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\left( {\frac{{2\left( {1 + \xi + {\xi ^2}} \right)}}{{\xi \left( {2\xi + 1} \right)}}} \right) \end{array} $ | (25) |
对于PBX厚壁球结构件, ξ≈1, 则可知, 式(25)是其所能承受的最大温度载荷。式(25)可改写成
| $ \Delta T\left| {_{\max }} \right. = \frac{{1 + \frac{1}{3}\tan \beta }}{{1 + \frac{2}{3}\tan \beta }}{\sigma _t}\frac{{1 - \nu }}{{E\alpha }}\psi \left( \xi \right) $ | (26) |
分析上述四种强度准则下的承受温差能力(13)、(17)、(20)、(25)式, 最大正应力准则只考虑了周向应力对材料结构强度的影响没有考虑径向应力、切向应力的影响, 在外壁破坏点处双轴拉伸状态用单轴拉伸破坏强度直接表示, 因此得出的承载能力偏大。Von-Mises准则考虑了偏应力对材料结构强度的影响, 忽略了体积应力影响, 因此其得出的承载能力比最大正应力准则略小, 若破坏点在外壁, 则结果一致。Mohr-Coulomb准则引入了拉压不对称系数, 考虑了径向应力的影响, 球对称下, 其得出承载能力与最大正应力准则一致。Drucker-Prager准则综合考虑了平均应力和偏应力对材料强度的影响, 若破坏点在外壁, 其可以分析双轴拉伸状态的破坏情况, 相同结构系数下, 该准则下得出的承受温差能力低于其他三种准则。
对于PBX厚壁球结构, 四种强度准则分析的破坏点都在外壁。根据PBX炸药双轴拉伸状态的强度极限比单轴略小, 只有Drucker-Prager准则能准确体现这一特点, 因此Drucker-Prager准则比其他三种准则更适合于PBX炸药。
6 承受温差能力分析根据四种强度准则分析讨论, 式(13)、(17)、(20)、(25)中
| $ \Delta T\left| {_{\max }} \right. = \eta {\sigma _{\rm{t}}}\frac{{1 - \nu }}{{E\alpha }}\psi \left( \xi \right) $ | (27) |
式中, η为由强度准则决定的系数, ψ(ξ)是结构系数, 无量纲参数, 与结构尺寸形状相关, 对于PBX厚壁球结构件, 有
| $ \Delta T\left| {_{\max }} \right. = \eta {\sigma _t}\left( T \right)\frac{{1 - \nu \left( T \right)}}{{E\left( T \right)\alpha \left( T \right)}}\psi \left( \xi \right) $ | (28) |
针对式(28)展开分析:
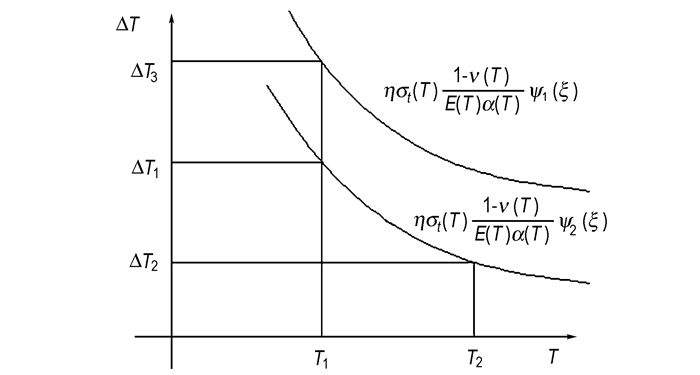
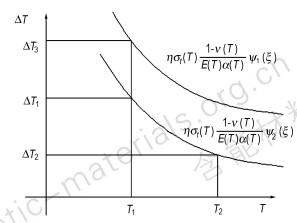
(1) 材料结构件承受温差能力是与材料特性是正相关的。若结构系数不变, 则提高拉伸强度和降低弹性模量有利于承载更大的温度差。根据文献[7], 可知拉伸强度对温度的敏感性比弹性模量高, 随着温度的升高, 拉伸强度下降比弹性模量下降更为明显, 故总体上, 随着温度的升高, PBX厚壁球结构件所能承受的温度差反而下降, 其示意图如图 4。故可知PBX厚壁球结构件在低温时能承受的温度载荷比高温时大。
|
图 4 结构件承受温差能力与材料性能及温度关系示意图 Fig.4 Relationship of the structure temperature carrying ability with material properties and temperature |
(2) 现比较常温时的三种PBX炸药的力学性能, 根据表 1, 可知PBX-C的弹性模量比PBX-A、PBX-E高一个数量级, 拉伸破坏强度高3~5倍, 而拉伸破坏应变却低一个数量级。根据此性能, 分析比较三种PBX的承受温差能力, 结合式(28), 在一定温度范围内(268~303 K), 有
| $ \begin{array}{l} \Delta T\left| {_{{\rm{PBX - A}}}} \right. = 29.7\eta \psi \left( \xi \right);\\ \Delta T\left| {_{{\rm{PBX - E}}}} \right. = 23.25\eta \psi \left( \xi \right);\\ \Delta T\left| {_{{\rm{PBX - C}}}} \right. = 5.326\eta \psi \left( \xi \right) \end{array} $ | (29) |
由式(29)可知: PBX-A的承受温差能力是PBX-C的5.6倍, PBX-E的承受温差能力是PBX-C的4.4倍。
现针对PBX-A厚壁球结构的承受温差能力进行计算。该PBX是由尺寸200 μm左右的HMX颗粒和少量高分子粘结剂等经一定工艺等压压缩而成的。其室温下拉伸破坏强度σt为1.8 MPa, 弹性模量E为0.68 GPa, 泊松比ν为0.4, 内摩擦角β为20°。取其热膨胀系数α为5.34×10-5 K-1。在应用工程中假设厚壁球结构件内壁半径ri为15 cm, 外壁半径re为25 cm, 则可知其半径比ξ为0.6, 其结构系数
| $ \begin{array}{l} \Delta T\left| {_{\max }} \right. = \eta {\sigma _t}\left( T \right)\frac{{1 - \nu \left( T \right)}}{{E\left( T \right)\alpha \left( T \right)}}\psi \left( \xi \right)\\ \;\;\;\;\;\;\;\;\;\; = 0.907 \times 1.8 \times \frac{{1 - 0.4}}{{680 \times 5.34 \times {{10}^{ - 5}}}} \times 2.97\\ \;\;\;\;\;\;\;\;\;\; = 80.1{\rm{K}} \end{array} $ | (30) |
即在室温下PBX-A厚壁球结构能承受环境变化的温度差为80.1K(不考虑温度变化引起的化学变化)。但考虑到PBX炸药力学性能随着温度的改变而改变, 故若外界环境温度升高, 则其所能承受的温度差应低于80.1 K; 若外界温度降低, 则其所能承受的温度差则高于80.1 K。但其具体温度环境下的失效破坏情况仍然需要大量实验数据来验证。
将同样的计算过程应用于PBX-E和PBX-C, 可以获知, 室温下, PBX-E厚壁球结构能承受环境变化的温度差为62.2 K, PBX-C厚壁球结构能承受环境变化的温度差为14.3 K。可见, 相对而言, PBX-A与PBX-E的承受温差能力都是较好的, 抵抗外界温度变化能力较强, 平时储运过程中的结构可靠性还是较高的; PBX-C的抵抗外界温度变化能力较低, 对外界温度变化敏感, 结构可靠性较低。
(3) 鉴于(28)式中随温度变化的材料参数过多, 根据文献[11]中可以将PBX炸药拉伸过程认为是线弹性的, 可将式(28)变换为:
| $ \Delta T\left| {_{\max }} \right. = \eta \frac{{{\sigma _t}\left( T \right)1 - \nu \left( T \right)}}{{E\left( T \right)\alpha \left( T \right)}}\psi \left( \xi \right) = \eta {\varepsilon _t}\left( T \right)\frac{{1 - \nu \left( T \right)}}{{\alpha \left( T \right)}}\psi \left( \xi \right) $ | (31) |
式(31)显示, PBX结构件的承受温差能力取决于拉伸破坏应变。在PBX生产加工配方调制中, 拉伸强度总是与弹性模量同步升降, 因此较难判断哪个参数占主导作用, 现采用拉伸破坏应变的表示方法, 避免了讨论拉伸强度与弹性模量的主导性, 将两个参数缩减为一个参数。故只需判断拉伸破坏应变的性能即可判断PBX结构件的承受温差能力, 也可指导生产中的配方调制。
室温下, 不同材料的PBX结构件承受温差能力的估算公式:
| $ \Delta T\left| {_{\max }} \right. = \eta {\varepsilon _t}\frac{{1 - \nu }}{\alpha }\psi \left( \xi \right) = 0.112 \times {10^5}{\varepsilon _t}\eta \psi \left( \xi \right) $ | (32) |
式中, εt为拉伸破坏应变。该公式仅适用于较低温度下, 因为较高温度下会提高材料的延展性, 从而使材料呈现较大塑性, 使得破坏应变增大, 从而会得出温度升高会导致承受温差能力增加的现象, 这与图 4矛盾。
(4) 结构能承受的最大温度载荷ΔT|max与结构系数ψ(ξ)也是相关的, 在材料特性(σt、E、ν、α)确定的前提下, 通过优化结构尺寸形状以提高ψ(ξ)值, 从而提高结构的承受温差能力。
7 结论(1) 在定常温度场下, 对PBX厚壁球结构件进行了热弹性分析, 并利用不同强度准则分析了热应力对特定结构的影响, 分析了其可能的破坏点及所能承受的最大温度差, 并给出了计算公式。对比发现, Drucker-Prager准则更适合于描述PBX炸药, 能描述PBX双轴拉伸强度比单轴拉伸强度略低的现象。为下一步研究PBX结构件在非定常温度场中, 或者以热能方式传导等具体状况的热应力研究奠定了基础。
(2) 通过研究特殊结构PBX厚壁球结构件的承受温差能力, 经过无量纲分析和分离乘式因子, 获知了PBX普通结构件承受温差能力与材料性能参数及结构系数之间的公式关系。根据该关系, 获知PBX-A的承受温差能力是PBX-C的5.6倍, PBX-E的承受温差能力是PBX-C的4.4倍; 可以对材料结构尺寸进行优化, 从而提高其承受温差能力。给出了PBX结构件承受温差能力的估算公式, 为工程上的PBX炸药及其结构生产设计应用提供参考。
| [1] |
罗景润. PBX的损伤、断裂及本构关系研究[D]. 绵阳: 中国工程物理研究院, 2001.
LUO Jing-run. Damage, fracture and constitutive relation of PBX[D]. Mianyang: China Academy of Engineering Physics, 2001. |
| [2] |
颜熹琳, 李敬明, 周阳, 等. 高聚物粘结炸药温湿度载荷加速老化试验研究[J].
含能材料, 2009, 17(4): 412-414. YAN Xi-lin, LI Jing-ming, ZHOU Yang, et al. Temperature and humidity load accelerated ageing test of polymer bonded explosive[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(4): 412-414. |
| [3] |
韦兴文, 周筱雨, 涂小珍, 等. HMX基PBX的温度环境适应性[J].
火炸药学报, 2012, 035(1): 15-18. WEI Xing-wen, ZHOU Xiao-yu, TU Xiao-zhen, et al. Temperature environmental adaptability of HMX based PBX[J]. Chinese Journal of Explosives & Propellants, 2012, 035(1): 15-18. |
| [4] |
屈均利, 刘向东. 低碳钢厚壁球壳热处理时的非定常应力分析[J].
煤矿机械, 2010, 31(7): 102-104. QU Jun-li, LIU Xiang-dong. Low carbon steel thick spherical shell structure unsteady stress analysis during heat treatment[J]. Coal Mine Machinery, 2010, 31(7): 102-104. |
| [5] |
Thompson D G, Deluca R, Brown G W. Time-temperature analysis, tension and compression in PBXs[J].
Journal of Energetic Materials, 2012, 30: 299-323. DOI:10.1080/07370652.2011.569831 |
| [6] |
Ellis K, Leppard C, Radesk H. Mechanical properties and damage evaluation of a UK PBX[J].
Journal of Materials Science, 2005, 40: 6241-6248. DOI:10.1007/s10853-005-3148-4 |
| [7] |
Drodge D R, Willianson D M, Palmer S J P, et al. The mechanical response of a PBX and binder: combining results across the strain-rate and frequency domains[J].
Journal of Physics D: Applied Physics, 2010, 43: 1-7. |
| [8] |
Williamson D M, Palmer S J P, Proud W G and Govier R K. 2009 Brazilian disc testing of a UK PBX approaching the glass transition temperature[C]//Shock Compression of Condensed Matter; AIP Conf. Proc. (Nashville, TN) (New York: AIP) 1195.
|
| [9] |
韦兴文, 周筱雨, 王培, 等. 温度对HMX基PBX炸药热膨胀系数和热导率的影响[J].
火炸药学报, 2012, 35(3): 33-37. WEI Xing-wen, ZHOU Xiao-yu, WANG Pei, et al. Effect of temperature to expansion coefficient and thermal conductivity of HMX based PBX[J]. Chinese Journal of Explosives & Propellants, 2012, 35(3): 33-37. |
| [10] |
Gruau C, Picart D, Belmas R. Ignition of a confined high explosive under low velocity impact[J].
International Journal of Impact Engineering, 2009, 36: 537-550. DOI:10.1016/j.ijimpeng.2008.08.002 |
| [11] |
唐维, 李明, 温茂萍, 等. 四种强度准则在高聚物粘结炸药强度分析中的适应性[J].
固体力学学报, 2013, 34(6): 550-555. TANG Wei, LI Ming, WEN Mao-ping, et al. Adaptability of four strength criterions in polymer bonded exprosives strength analysis[J]. Chinese Journal of Solid Mechanics, 2013, 34(6): 550-555. |
| [12] |
唐维, 颜熹琳, 李明, 等. 间接三轴拉伸破坏试验分析某TATB基PBX强度准则适应性[J].
含能材料, 2015, 23(6): 532-536. TANG Wei, YAN Xi-lin, LI Ming, et al. Adaptability analysis of strength criterion on TATB Based PBX by indirect triaxial tensile collapse test[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2015, 23(6): 532-536. DOI:10.11943/j.issn.1006-9941.2015.06.005 |
| [13] |
王鹏飞, 黄西成, 何颖波, 等. 基于线性Drucker-Prager模型的PBX准静态弹塑性变形分析[J].
含能材料, 2015, 23(5): 464-471. WANG Peng-fei, HUANG Xi-cheng, HE Ying-bo, et al. Quasi-static elastoplastic deformation analysis of PBX : Applicability of Linear Drucker-Prager model[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2015, 23(5): 464-471. DOI:10.11943/j.issn.1006-9941.2015.05.012 |
| [14] |
唐维, 颜熹琳, 李明, 等. TATB基PBX的单轴主特征破坏参数识别研究[J].
含能材料, 2015, 23(8): 766-770. TANG Wei, YAN Xi-lin, LI Ming, et al. Identification of uniaxial main characteristic failure parameter on TATB-based PBX[J]. Chinese Journal of Energetic materials(Hanneng Cailiao), 2015, 23(8): 766-770. DOI:10.11943/j.issn.1006-9941.2015.08.011 |
| [15] |
李维特, 黄保海, 毕仲波.
热应力理论分析及应用[M]. 北京: 中国电力出版社, 2004: 95-98.
LI Wei-te, HUANG Bao-hai, BI Zhong-bo. The theory analysis and application of thermal stress[M]. Beijing: Chinese Electric Power Press, 2004: 95-98. |
| [16] |
徐芝纶.
弹性力学简明教程[M]. 北京: 高等教育出版社, 2008: 152-155.
XU Zhi-lun. A concise course in Elasticity[M]. Beijing: High education press, 2008: 152-155. |
A thermoelastic deformation analysis of polymer bonded explosive (PBX) thick wall spherical shell structure in steady temperature field was launched and the failure damage status of the structure under the action of thermal stress was discussed. The temperature difference carrying capacity and first failure point position of thick wall spherical shell structure were analyzed by strength criterions. The rule of the temperature difference carrying capacity of ordinary PBX structure was obtained via related structure shape and size parameters factors.




