2. Southwest University of Science and Technology, Mianyang 621010, China;
3. School of Sciences, Nanjing University of Science and Technology, Nanjing 210094, China
2. 西南科技大学, 四川 绵阳 621010;
3. 南京理工大学理学院, 江苏 南京 210094
Polymer bonded explosives(PBXs), a kind of energetic material, are mainly composed of explosive crystal, polymer, plasticizer, and desensitizer. The mass ratio of explosive crystal is often more than 90%. Except for energy supply, PBXs in weapon systems also have to bear thermal-mechanical loads during assembly, transportation, storage and usage. Damaged explosive parts may induce danger and affect the propagation of detonation waves [1]. Constitutive model is the basis to study the mechanical behaviors of materials, and it plays an important role in evaluating the mechanical response of structural components in service environment, especially in simulation code for engineering analysis.
The constitutive response of PBXs is very complex to model because of the nonlinearity and asymmetry of their stress-strain curves. In 1984, a constitutive model of PBX was established by Browning et al [2]. This model was developed in 1989, but it is a one-dimensional model [3]. The one known as the ViscoSCRAM [3] is the most famous model for PBXs in recent years, and it is still working now according to the studies [4-5]of Los Alamos National Laboratory(LANL). It is based on capturing time-dependent behavior by combining a viscoelastic model with the accumulation of internal damage. Actually, the ViscoSCRAM model could not fit the test results well now [6-7], because its parameters are difficult to confirm. Moreover, although many studies on stress-strain curves of typical PBXs have been reported [8-11], no research has studied the universal constitutive model of explosive materials considering both tension and compression. Normally, tension and compression are studied independently, and the tensile curve at room temperature is often viewed as linear [12-13]. As a result, the calculation process may go against with practical behaviors and cause errors. There are certainly many other investigations [14-15]about this relationship, but just like what Devin Shunk said in his report [16], even with all of the exploratory work, the constitutive models for PBXs are still lacking. Thus, Boltzmann function is proposed in this paper to establish a uniaxial nonlinear constitutive model for typical PBXs under quasi-static loading, both tension and compression were considered in the model.
2 Modeling 2.1 Mechanical Properties of Typical PBXsPBX-X, PBX-9502, LX-17, PBX-9501, and EDC-37 are five typical PBXs of different countries, their names and components are listed in Table 1. The stress-strain curves of Chinese PBX-X in present paper have similar common features with the rest four, and they are obtained by universal testing methods. A typical stress-strain curve of PBX-X, including both tension and compression data at 50 ℃, is shown in Fig. 1. The curves are typically S-shaped with obvious nonlinearity. The modulus decreases gradually with load increasing. Moreover, the curve also shows obvious asymmetry by the absence of a plateau when the material is under tension. After the maximum compression stress is reached, the stress gradually decreases with the strain increasing continuously until a sudden failure happens to the material.
| Tab.1 Information of the five PBXs |

|
Fig.1 Tension-compression stress-strain curves of China′s PBX-X at 50 ℃ |
From Fig. 1, we know that the typical stress-strain behaviour of PBXs is an S-shaped curve with nonlinearity and asymmetry. As typical S-shaped curve functions, Boltzmann sigmoid, Gaussian cumulative, and Lorentz cumulative are commonly used to describe the transition behavior of some physical quantities, and they have been widely applied in the fields of medicine, biology, agriculture, physics, and chemistry [17-18]. Their mathematical expressions [18] are given in Eqs. (1), (2) and (3), respectively:
| $y\left( x \right) = \frac{{{Y_1} - {Y_2}}}{{1 + {{\rm{e}}^{\left( {x - {x_0}} \right)/{\rm{d}}x}}}} + {Y_2}$ | (1) |
| $y\left( x \right) = \frac{{\left( {{Y_2} - {Y_1}} \right){\rm{arctan}}\left( {\left( {\left( {x - {x_0}} \right)/{\rm{d}}x} \right) + \left( {{\rm{\pi }}/2} \right)} \right)}}{{\rm{\pi }}} + {Y_1}$ | (2) |
| $y\left( x \right) = \frac{{{Y_2} - {Y_1}}}{2}\left( {1 + \frac{1}{{\sqrt {\rm{\pi }} }}\int_0^{\frac{{x - {x_0}}}{{\sqrt 2 {\rm{d}}x}}} {{{\rm{e}}^{ - {t^2}}}{\rm{d}}t} } \right) + {Y_1}$ | (3) |
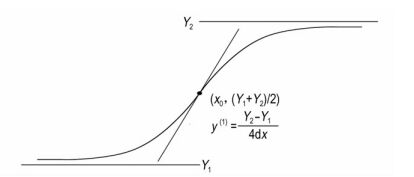
The physical significance of each parameter in theseEqs is the same: x is the independent variable, whereas y is the dependent variable. Four undetermined coefficients are used: Y1 and Y2 are the theoretical lower limit and upper limit of function y, respectively; x0 is the midpoint of x; and dx is used to represent the degree of curve changes. The rate of curve at x0 is proportional to 1/dx. All of the three functions describe the S-shaped curve shown in Fig. 2 in different mathematical forms.
|
Fig.2 Typical S-shaped curve and physical significance of parameters |
When y denotes stress and x denotes strain, Boltzmann sigmoid, Gaussian cumulative, and Lorentz cumulative can be used as the mathematical expressions of the constitutive model of materials with an S-shaped stress-strain curve. Given that these functions describe the curve of same type, the Boltzmann function, which is the simplest one, is adopted in this work to describe the constitutive model of PBXs. The Boltzmann function, which considers both tension and compression, conforms to the mathematical characteristics of PBXs′ stress-strain curves. More importantly, it is convenient to determine the values of undetermined coefficients, because their physical significance is relatively definite. The constitutive model based on the Boltzmann function could be expressed as:
| $\sigma = \frac{{{\sigma _{{\rm{ccs}}}} - {\sigma _{{\rm{tcs}}}}}}{{1 + {{\rm{e}}^{\alpha \varepsilon + \beta }}}} + {\sigma _{{\rm{tcs}}}}$ | (4) |
where σ and ε are the stress (MPa) and strain (dimensionless factor), respectively (positive in tension and negative in compression); the four undetermined coefficients, namely, σccs, σtcs, β, and α are the theoretical lower and upper limits of stress (MPa) correction factor of stress-strain at zero point (dimensionless factor) and the modulus correlation coefficient (dimensionless factor), respectively. The initial values can be determined via the following method:
(1) σccs and σtcs are the compressive and tensile critical stresses, respectively. For ductile materials with evident tensile and compressive plateau in stress-strain curves, the values of σccs and σtcs are the compressive and tensile strengths. Given the brittle nature of PBXs, only the compressive plateau is observed (i.e., no tensile plateau). The value of σccs is the compressive strength. The initial value of σtcs is larger than its tensile strength. It is an infinite virtual value and is inversely proportional to the compressive strength.
(2) The physical significance of β, the correction coefficient of the stress-strain at zero point, is that when the strain is zero, the stress is also zero. This relationship is the basic attribute of the quasistatic constitutive model. When zero strain and zero stress are substituted into Eq.(4), Eq.(5) can be obtained. Particularly, if the tensile stress-strain curve and compressive stress-strain curve are perfectly symmetrical and the absolute values of σccs and σtcs are equal, then β=0.
| ${{\rm{e}}^\beta } = - \frac{{{\sigma _{{\rm{ccs}}}}}}{{{\sigma _{{\rm{tcs}}}}}} \Leftrightarrow \beta = {\rm{ln}}\left( { - \frac{{{\sigma _{{\rm{ccs}}}}}}{{{\sigma _{{\rm{tcs}}}}}}} \right)$ | (5) |
(3) The mathematical expression of the modulus [Eq.(6)] can be obtained from Eq.(4). The modulus is a variable that changes with strain, and its maximum value is achieved at the zero strain point. At this point, Eq.(7) is the mathematical expression of the modulus correlation coefficient α. When the elasticity modulus E0 close to the zero point is substituted into Eq.(7), the initial value of α can be determined. Particularly, when β=0, Eq.(7) can be simplified into Eq.(8).
| $E = \frac{{{\rm{d}}\sigma }}{{{\rm{d}}\varepsilon }} = - \frac{{\alpha {{\rm{e}}^{\alpha \varepsilon + \beta }}({\sigma _{{\rm{ccs}}}} - {\sigma _{{\rm{tcs}}}})}}{{{{(1 + {{\rm{e}}^{\alpha \varepsilon + \beta }})}^2}}}$ | (6) |
| ${E_0} = \frac{{\alpha {{\rm{e}}^\beta }({\sigma _{{\rm{tcs}}}} - {\sigma _{{\rm{ccs}}}})}}{{{{(1 + {{\rm{e}}^\beta })}^2}}} \Leftrightarrow \alpha = \frac{{{E_0}{{(1 + {{\rm{e}}^\beta })}^2}}}{{{{\rm{e}}^\beta }({\sigma _{{\rm{tcs}}}} - {\sigma _{{\rm{ccs}}}})}}$ | (7) |
| ${E_0} = \frac{{\alpha ({\sigma _{{\rm{tcs}}}} - {\sigma _{{\rm{ccs}}}})}}{4} \Leftrightarrow \alpha = \frac{{4{E_0}}}{{{\sigma _{{\rm{tcs}}}} - {\sigma _{{\rm{ccs}}}}}}$ | (8) |
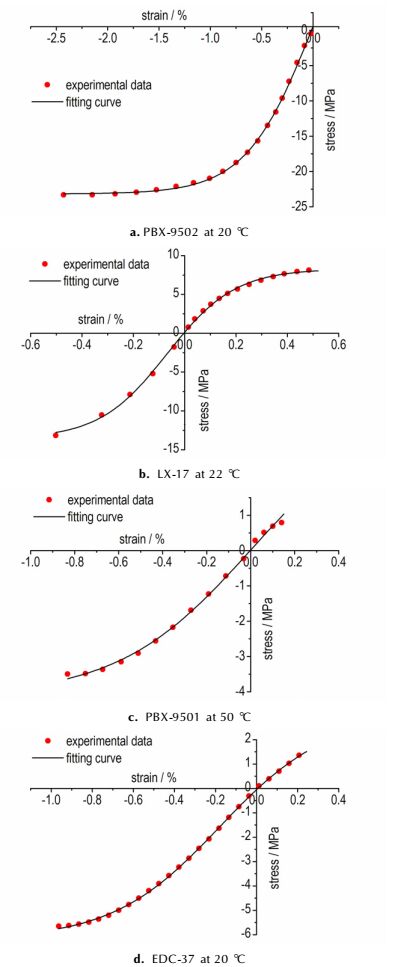
This Boltzmann function based nonlinear tension-compression constitutive model is described as Eq.(4), its initial values of the parameters are determined via test data and the methods introduced above. Finally, the test data [8-11] and fitting curves of PBX-X, PBX-9502, LX-17, PBX-9501, and EDC-37 are shown in Fig. 3 and Fig. 4, respectively. The testing temperature and strain rate, as well as the fitting results and its applicable range, are listed in Table 2. All of the values of the adjusted R-square are higher than 0.99, thereby the fitting results of both the 1, 3, 5-triamino-2, 4, 6-trinitrobenzene (TATB) -based PBXs (PBX-901, PBX-9502, and LX-17) and octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine (HMX)-based PBXs (PBX-9501 and EDC-17) are satisfying. The Boltzmann function based constitutive model can be widely used in different PBX materials.

|
Fig.3 Experimental data and fitting curve for PBX-X at 50 ℃ |
|
Fig.4 Experimental data and fitting curves for PBX-9502, LX-17, PBX-9501 and EDC-37 |
Additionally, the above test data of PBX-X is obtained from laboratory test, and the rest data is collected from literatures. In practical engineering, the mechanical behaviors of explosive structural components are calculated and predicted via numerical simulation. The constitutive model is required to describe the stress-strain relationship precisely at least in the zone from the maximum compressive stress to the maximum tensile stress, which can be satisfied by the Boltzmann function used above. However, the region from the maximum compression stress to the sudden failure cannot be described mathematically by the established constitutive model yet.
| Tab.2 Constitutive model parameters for the five PBXs |
(1) The uniaxial quasi-static tension-compression stress-strain curves of PBXs have evident nonlinearity, and these curves have poor asymmetry and exhibit a typical S-shape.
(2) Boltzmann function is a widely used typical S-shaped curve function, the constitutive model deduced based on the Boltzmann function has four undetermined coefficients (namely, the theoretical lower limit of stress, the theoretical upper limit of stress, correction factor of stress-strain at zero point and the modulus correlation coefficient.), their initial values can be determined by theoretical analysis without fitting.
(3) The uniaxial nonlinear constitutive models of five typical PBXs (PBX-X, PBX-9502, LX-17, PBX-9501, and EDC-37) were established according to their stress-strain curves. The values of the adjusted R-square are higher than 0.997, it indicated that this constitutive model based on Boltzmann function is capable of describing the stress-strain relationship at different temperatures and strain rates, and it can be widely used in different PBX materials as a universal constitutive model, in which both tension and compression nonlinearity are considered.
| [1] | Scott I Jackson, Larry G. Runaway reaction due to gas-dynamic choking in solid explosive containing a single crack[J]. Proceeding of the Combustion Institute, 2009, 32: 2307-2313. DOI:10.1016/j.proci.2008.05.089 |
| [2] | Browning R, Gurtin M, Williams W. A one-dimensional viscoplastic constitutive theory for filled polymers[J]. International Journal of Solids and Structures, 1984, 20: 921-934. DOI:10.1016/0020-7683(84)90081-7 |
| [3] | Browning R, Gurtin M, Williams W. A model for viscoplastic materials with temperature dependence[J]. International Journal of Solids and Structures, 1989, 25: 441-457. DOI:10.1016/0020-7683(89)90058-9 |
| [4] | Bennett J, Haberman K, Johnson J, et al. A constitutive model for the non-shock ignition and mechanical response of high explosives[J]. Journal of the Mechanics and Physics of Solids, 1998, 46: 2303-2322. DOI:10.1016/S0022-5096(98)00011-8 |
| [5] | Hackett R, Bennett J. An implicit finite element material model for energetic particulate composite materials[J]. International Journal for Numerical Methods in Engineering, 2000, 49: 1191-1209. DOI:10.1002/(ISSN)1097-0207 |
| [6] | ZHANG Yan-Geng, LOU Jian-Feng, HONG Tao. Modification of Visco Statistical Crack Mechanics for PBXs[J]. Chinese Journal of High Pressure Physics, 2015, 29(1): 9-14. |
| [7] | GAO Jun, HUANG Zai-xing. Parameter identification for viscoelastic damage constitutive model of PBX[J]. Engineering Mechanics, 2015, 32(2): 201-206. |
| [8] | Skidmore C B, Idar D J, Buntain G A, et al. Sander. Aging and PBX 9502[R]. Los Alamos National Laboratory report LA-UR-98-1206, 1998. |
| [9] | Groves S, Cunningham B. Tensile and Compressive Mechanical Properties of Billet Pressed LX17-1 as a Function of Temperature and Strain Rate[R]. Lawrence Livermore National Laboratory report UCRL-ID-137477, 2000. |
| [10] | Partha Rangaswamy, Darla G. Thompson, Cheng Liu, et al. Modeling the mechanical response of PBX 9501[J]. Proceeding of 14th International Detonation Symposium, 2010, 52(3): 174-183. |
| [11] | Ellis K, Leppard C, Radesk H. Mechanical properties and damage evaluation of a UK PBX[J]. Journal of Materials Science, 2005, 40: 6241-6248. DOI:10.1007/s10853-005-3148-4 |
| [12] | TANG Wei, YAN Xi-lin, LI Ming, et al. Adaptability analysis of strength criterion on TATB based PBX by indirect triaxial tension collapse test[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2015, 23(6): 532-536. |
| [13] | TANG Wei, LI Ming, WEN Mao-ping, et al. Adaptability of four strength criterions in polymer bonded explosives strength analysis[J]. Acta Mechanica Solida Sinica, 2013, 34(6): 550-556. |
| [14] | Darnell S Oh, C Hrousis, B Cunningham, et al. A constitutive model for long time duration mechanical behavior in insensitive high explosives[R]. Lawrence Livermore National Laboratory report LLNL-CONF-425382, 2010. |
| [15] | TANG Ming-feng, PANG Hai-yan, LAN Lin-gang, et al. Constitutive behavior of RDX-based PBX with loading-history and loading-rate effects[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2016, 24(9): 832-837. |
| [16] | Shunk Devin. PBX 9502 literature review: An engineering perspective[R]. Los Alamos National Laboratory report LA-UR-13-21673, 2013. |
| [17] | Annette A A vanKuijk, Chantal D Bakker, Jan C M Hendriks, et al. Definition dependent properties of the cortical silent period in upper-extremity muscles[J]. Journal of Neuroengineering and Rehabilitation, 2014, 11: 1-9. DOI:10.1186/1743-0003-11-1 |
| [18] | Tao Zhou, Leilei Peng, Yongcheng Liu, et al. An insight into the sequential order in 2D correlation spectroscopyusing polymer transitions: Boltzmann Sigmoid, Gaussian Cumulative, Lorentz Cumulative, and Asymmetric Sigmoid. Findings inexperiments and simulations[J]. Vibrational Spectroscopy, 2014, 70: 137-161. DOI:10.1016/j.vibspec.2013.12.001 |
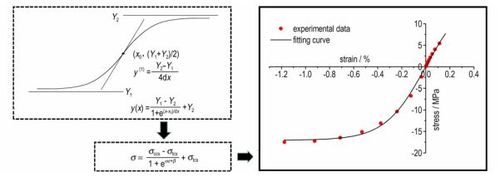
A uniaxial nonlinear consititutive model was deduced based on Boltzmann function. The nonlinearity and asymmetry of quasi-static stress-strain curves of five typical PBXs (PBX-X, PBX-9502, LX-17, PBX-9501, and EDC-37), were described by this model.




