2. 北京应用物理与计算数学研究所, 北京 100088
2. Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
凝聚相炸药的拐角爆轰一直是爆轰波研究和武器装备设计的重点关注的问题, 涉及到拐角的绕射、熄爆及重新起爆。从20世纪60年代, 国内外针对凝聚相炸药拐角爆轰进行了大量的数值模拟研究。Tarver[1]采用点火增长模型对不同炸药的拐角绕射现象进行了数值模拟, 讨论了不同拐角下的反应延迟; Tang等[2]把显式的热点模型应用到DYNA2D程序中, 模拟了PBX-9502炸药中爆轰波绕射情况; 冯长根[3]利用二维拉格朗日数值程序2DLE, 对混合炸药中爆轰波拐角绕射现象进行了数值模拟; 孙承纬[4]利用程序WSU, 对几种炸药的拐角爆轰现象进行了数值模拟。以上研究集中讨论了凝聚相炸药拐角爆轰的绕射现象, 给出了不同拐角下对爆轰波衍射波结构的影响, 但由于采用了经典的爆轰物理模型, 忽略了多介质的影响, 没有重点考虑拐角区域的熄爆和重新起爆过程。
由于拐角的存在, 爆轰波在绕过拐角过程可能发生熄爆, 实验上并不能很好解释“死区”效应[5], 尤其很难定义“死区”的作用尺寸和作用时间。Banks[6-7]从数值角度分析了LX-17炸药在拐角处的绕射过程, 给出了拐角内壁面区域炸药状态变化规律, 发现了沿内壁面的的熄爆和二次起爆现象, 但Banks采用了基于质量分数的多物质爆轰模型[7], 在多介质混合热力学状态计算时存在数值不收敛, 不能准确的描述爆轰波流场与化学反应的耦合相互作用。
为此, 本研究将质量分数的多物质爆轰模型改进为体积分数, 以消除多介质混合区域的计算误差, 并发展适用于多介质爆轰反应区计算的平衡迭代方法, 自主搭建高性能的并行模拟软件DESEM。通过高效高分辨率的数值模拟研究拐角区域爆轰流场与化学反应的耦合-解耦过程, 对比分析了爆轰衍射的波阵面结构, 并讨论了了拐角爆轰的熄爆和二次起爆的机理。
2 凝聚相炸药爆轰物理模型 2.1 守恒型方程凝聚相炸药爆轰是极端条件下发生的复杂动力学响应过程, 涉及到炸药、爆轰产物和周围介质等多种物质; 由于爆轰过程的高速瞬态性, 可以忽略此过程的粘性和热传导过程, 将爆轰过程的控制方程写成如下守恒形式:
| $\begin{eqnarray} \frac{∂\boldsymbol{u}}{∂\boldsymbol{t}}+\frac{∂\boldsymbol{f}(\boldsymbol{u})}{∂\boldsymbol{x}}+\frac{∂\boldsymbol{g}(\boldsymbol{u})}{∂\boldsymbol{y}}+\frac{∂\boldsymbol{h}(\boldsymbol{u})}{∂\boldsymbol{z}}=\boldsymbol{H}+\boldsymbol{S} \end{eqnarray}$ | (1) |
式中,u为守恒型变量, f, g, h为不同方向的流通量, H为方程源项, S为几何源项(柱坐标情况存在, 笛卡尔坐标下为0);对于两种物质情况下, 各矢量可以写成如下形式:
| $\begin{eqnarray} &&\boldsymbol{u}=\left\{ \begin{array}{l} z_{1}ρ_{1}\\ z_{2}ρ_{2}\\ ρu\\ ρv\\ ρw\\ ρE\\ z_{1}\\ z_{2}ρ_{2}λ \end{array} \right\}, \boldsymbol{f}=\left\{ \begin{array}{l} z_{1}ρ_{1}u\\ z_{2}ρ_{2}u\\ ρu^{2}+p\\ ρuv\\ ρuw\\ u(ρE+p)\\ z_{1}u\\ z_{2}ρ_{2}λu \end{array} \right\}, \boldsymbol{g}=\left\{ \begin{array}{l} z_{1}ρ_{1}v\\ z_{2}ρ_{2}v\\ ρuv\\ ρv^{2}+p\\ ρvw\\ v(ρE+p)\\ z_{1}v\\ z_{2}ρ_{2}λv \end{array} \right\},\\ &&\boldsymbol{h}=\left\{ \begin{array}{l} z_{1}ρ_{1}w\\ z_{2}ρ_{2}w\\ ρuw\\ ρvw\\ ρw^{2}+p\\ w(ρE+p)\\ z_{1}w\\ z_{2}ρ_{2}λw \end{array} \right\}, \boldsymbol{H}=\left\{ \begin{array}{l} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ z_{1}∇·(u,v,w)\\ K \end{array} \right\},\\ &&\boldsymbol{S}=-\frac{v}{y}\left\{ \begin{array}{l} z_{1}ρ_{1}\\ z_{2}ρ_{2}\\ ρu\\ ρv\\ ρw\\ ρE+p\\ z_{2}ρ_{2}λ\\ 0 \end{array} \right\} \end{eqnarray}$ |
式中,ρ为表示密度, (u, v, w)为速度, p为压力, E为单位质量的总能, 定义为E=e+1/2(u2+v2+w2), e为单位质量的内能; λ为反应物质量分数, K反应源项, z表示物质的体积分数、下标1和2对应物质1和2, 且满足z1+z2=1;不同的物质界面处满足温度和压力平衡, 当考虑到物质2由反应物α到产物β的过程, 总体的比内能和密度满足如下条件:
| $\begin{eqnarray} ρe=z_{1}ρ_{1}e_{1}+z_{2}ρ_{2}e_{2}=z_{1}ρ_{1}e_{1}+z_{2}ρ_{2}(λe_{α}+(1-λ)e_{β}) \end{eqnarray}$ | (2) |
| $\begin{eqnarray} ρ=z_{1}ρ_{1}+z_{2}ρ_{2},~~~~\frac{1}{ρ_{2}}=\frac{λ}{ρ_{α}}+\frac{1-λ}{ρ_{β}} \end{eqnarray}$ | (3) |
控制方程(1)包含了质量分数和体积分数, 可以描述多种物质的动力学响应过程; 当忽略物质的化学反应过程, 该可退化为描述多介质可压缩流体的五方程模型; 当仅考虑炸药的爆轰过程, 以上方程可退化为反应流欧拉方程。
2.2 状态方程对于凝聚相炸药, 各种物质的状态方程统一写成Mie-Grüneisen的形式[8]:
| $\begin{eqnarray} p(ρ,e)=p_{\text{ref}}(ρ)+\mathit{Г}(ρ)ρ(e_{\text{ref}}(ρ)) \end{eqnarray}$ | (4) |
式中,Г为材料参数, pref和eref分别对应材料在等熵曲线或雨贡扭曲线上的压力和内能, 利用状态方程可以得到温度:
| $\begin{eqnarray} T=\frac{p-p_{\text{ref}}}{ρГC_{V}} \end{eqnarray}$ | (5) |
采用JWL状态方程描[9]述高压状态下固体炸药和气体爆轰产物的状态, 写成Mie-Grüneisen形式为:
| $\begin{eqnarray} p_{\text{ref}}(ρ)=A\text{exp}(\frac{-R_{1}ρ_{0}}{ρ})+B\text{exp}(\frac{-R_{2}ρ_{0}}{ρ}) \end{eqnarray}$ | (6) |
| $\begin{eqnarray} e_{\text{ref}}(ρ)=\frac{A}{ρ_{0}R_{1}}\text{exp}(\frac{-R_{1}ρ_{0}}{ρ})+\frac{B}{ρ_{0}R_{2}}\text{exp}(\frac{-R_{2}ρ_{0}}{ρ}) \end{eqnarray}$ | (7) |
| $\begin{eqnarray} \mathit{Γ}(ρ)=\mathit{Γ}_{0} \end{eqnarray}$ | (8) |
在炸药反应过程, 参考内能需要考虑反应过程中的能量释放Q, 针对固体炸药参考内能变为eref-Q。
2.3 炸药反应模型凝聚相炸药爆轰的化学反应过程非常复杂, 本研究采用Lee和Tarver提出的点火和成长反应率模型[10], 该模型包含了两项反应模型和三项反应模型。两项反应模型形式为:
| $\begin{eqnarray} \text{d}F/\text{d}t=-K=I(1-F)^{a}(ρ/ρ_{0}-1)^{x}+G(1-λ)^{b}λ^{c}p^{y} \end{eqnarray}$ | (9) |
式中, F=1-λ为产物的质量分数, I, G, b, c, d, x, y为炸药相关常数。该模型包含点火项和增长项, 可以描述持续脉冲冲击起爆的过程, 但该模型在描述短脉冲的冲击起爆时与实验相差较大, 因此又将以上模型修改为三项式, 形式为:
| $\begin{eqnarray} \text{d}F/\text{d}t&=&I(1-F)^{b}(ρ/ρ_{0}-1-a)^{x}H(F_{IG\text{max}}-F)+\\ &&G_{1}(1-F)^{c}F^{d}p^{y}H(F_{G1\text{max}}-F)+\\ &&G_{2}(1-F)^{e}F^{g}p^{z}H(F-F_{G2\text{max}}) \end{eqnarray}$ | (10) |
式中,H为Heaviside函数, I, G1, G2, a, b, c, d, e, g, x, y和z为炸药相关常数。FIGmax, FG1max, FG1max为常数, 该模型可以描述短脉冲冲击起爆过程中的热点成核、成长以及汇合三个阶段。
3 数值计算方法对于方程的离散采用基于非结构网格有限体积方法, 守恒型方程(1)中除体积分数控制方程都具有双曲方程的性质, 因此数值计算可以在空间上采用基于HLLC黎曼求解器的Godunov格式, 并利用MUSCL-Hancock格式扩展到二阶精度, 时间层上采用二阶精度的Runge-Kutta方法[11]。
体积分数可以描述炸药的外部介质的响应过程, 暂不属于本研究讨论范围。针对炸药的反应过程, 化学反应区内压力、温度等物理量的准确计算是爆轰模拟的关键。由于该区域内同时存在未反应固体炸药(s)和气体爆轰产物(g), 当满足T=Ts(νs, es)=Tg(νg, eg)和p=ps(νs, es)=pg(νg, eg)时, ν为比容, 热力学平衡状态要求下式收敛:
| $\begin{eqnarray} \left\{\begin{array}{c} p_{g}-p_{s}\\ T_{g}-T_{s} \end{array}\right\}= \left[\begin{array}{c} \frac{∂p_{s}}{∂v_{s}}-\frac{∂p_{g}}{∂v_{s}}&\frac{∂p_{s}}{∂e_{s}}-\frac{∂p_{g}}{∂e_{s}}\\ \frac{∂T_{s}}{∂v_{s}}-\frac{∂T_{g}}{∂v_{s}}&\frac{∂T_{s}}{∂e_{s}}-\frac{∂T_{g}}{∂e_{s}} \end{array}\right] \left\{\begin{array}{c} δv_{s}\\ δe_{s} \end{array}\right\} \end{eqnarray}$ | (11) |
计算中采用Newton-Raphson方法[12]迭代实现平衡条件。
另外, 考虑到大规模爆轰问题由于计算模型复杂所导致的运行效率问题, 以上数值算法基于JAUMIN框架开发, 并集成了高效非结构网格数据结构、索引算法和动态负载平衡, 可以实现数万核的并行计算。
4 模型和方法验证应用以上物理模型和数值方法模拟PBX9404炸药的爆轰, 计算模型的尺寸取为[0, 20] mm×[0, 4] mm。初始时刻在炸药左端2 mm内以CJ条件起爆炸药, 右端为未反应炸药, 初始条件如表 1。左右边界为连续边界条件, 固体炸药和反应产物均采用JWL状态方程, 化学反应率模型采用两项点火增长反应率模型, 参数如表 2。
| 表 1 PBX9404初始条件设置 Tab.1 Setting of initial conditions for PBX9404 |
| 表 2 PBX9404状态方程和反应率模型参数 Tab.2 Equation of state and reaction rate model parameters for PBX9404 |
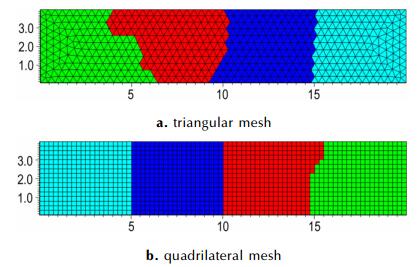
数值计算可以采用三角形图 1a、四边形网格图 1b, 以四核并行为例, 不同颜色代表对应着并行计算过程的处理器不同, 说明数值程序能够实现多核并行。为了测试网格收敛性性情况, 网格取为四边形网格, 划分方式分别为40 cells·mm-1和80 cells·mm-1。
|
图 1 不同网格单元并行分区 Fig.1 Parallel partition of different mesh units |
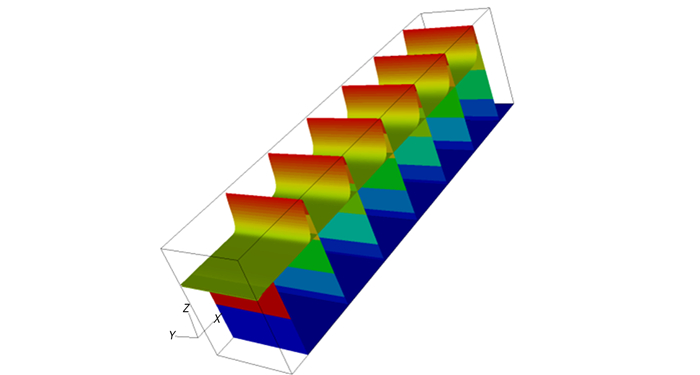
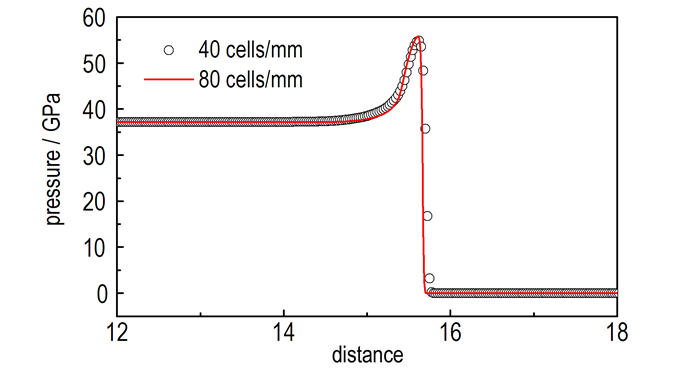
图 2给出了网格数为40 cells·mm-1的压力分布随时间的变化, 由图 2可以看出, 当时间大于0.50 μs时爆轰趋于稳定, 图 3显示在1.20 μs时刻不同网格分辨率下的压力分布, 从图 3中可以看出网格分辨率为40 cells·mm-1和80 cells·mm-1两种情况的压力分布基本一致, 说明采用以上模型和方法计算凝聚相炸药爆轰具有较好的网格的收敛性。
|
图 2 爆轰波在不同时刻的压力分布(t=0 μs到1.8 μs,Δt=0.3 μs) Fig.2 The pressure distribution of detonation wave at different time(t=0 μs to 1.8 μs, Δt= 0.3 μs) |
|
图 3 t=1.2 μs时不同网格划分下的压力曲线 Fig.3 The pressure curves under different mesh pertition at t=1.2 μs |
表 3给出了在40 cells·mm-1划分条件下该炸药Von Neumann峰值的计算结果与实验结果, 由表 3可见, 计算结果与实验值吻合较好, 因此, 本研究所采用的模型和方法能够正确的预测凝聚炸药的起爆及爆轰波传播的关键特征, 证明了物理模型和计算方法的合理性。
| 表 3 PBX9404 Von Neumann峰值计算结果与实验结果的误差 Tab.3 The errors between computational results and experimental ones of the Von Neumann value of PBX9404 |
炸药选取为PBX-9404, 具体参数见表 1和表 2。计算模型的尺寸取为[0, 12] mm×[8, 12] mm的直筒和不同的拐角区域, 直筒左端用CJ状态起爆作为初始条件, 爆轰波达到拐角位置时的时间为0.40 μs, 已经成长为稳定爆轰波。左端为入流边界条件, 右端为出流边界条件, 其余边界均为固壁边界, 计算中采用四边形网格, 网格分辨率为50 cells·mm-1。
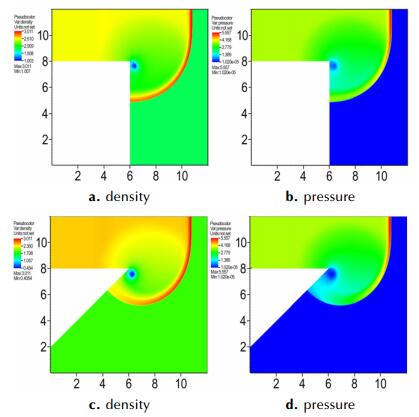
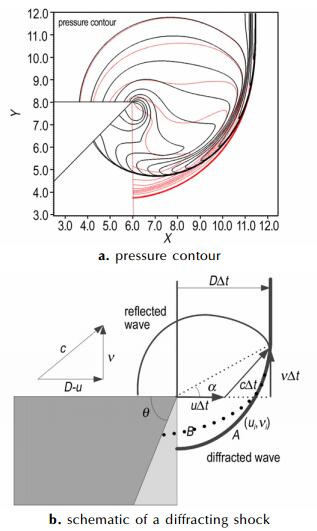
5.1 拐角波阵面研究图 4为90°和135°拐角绕射爆轰波密度和速度分布, 从图 4可以看出, 稳定的平面爆轰波由于受到拐角影响发生衍射, 衍射产生的稀疏波引起密度降低, 波阵面变的弯曲, 对比不同拐角发现, 拐角较大时对于爆轰波的稀疏作用更明显。绕射后的稀疏波可以根据激波的衍射理论得到, 已知激波后声速c、粒子速度u和未被扰动的激波速度D, 如图 5, 由图 5可以得到稀疏角α的关系满足:
| $\begin{eqnarray} \text{tan}α=\frac{v}{D}=\frac{\sqrt{c^{2}-(D-u)^{2}}}{D} \end{eqnarray}$ |
|
图 4 90°和135°拐角绕射爆轰波密度和压力分布 Fig.4 The distribution of density and pressure for diffraction detonation wave around the 90° and 135° corner |
|
图 5 90°和135°拐角绕射压力等高线对比和爆轰波衍射示意图 Fig.5 Comparison of diffraction pressure contour and the diffraction schematic of deonation wave at the 90° and 135° corner |
由α可以得到侧向冲击波的传播距离和时间, 对于爆轰波来说, 假设满足C-J爆轰, 根据激波传播的自相似性, 可以采用以上理论来追踪拐角爆轰波阵面; 当拐角为任意角度θ, 任意点流场速度为u时, 可以得到波阵面距离函数φ(x, y)满足:
| $\begin{eqnarray} \frac{∂φ}{∂t}+\boldsymbol{u}·\frac{∇φ}{\left|∇φ\right|}\left|∇φ\right|=0 \end{eqnarray}$ |
结合数值模拟结果可以得到波阵面形状(曲率、法向)和冲击波强度的关系。
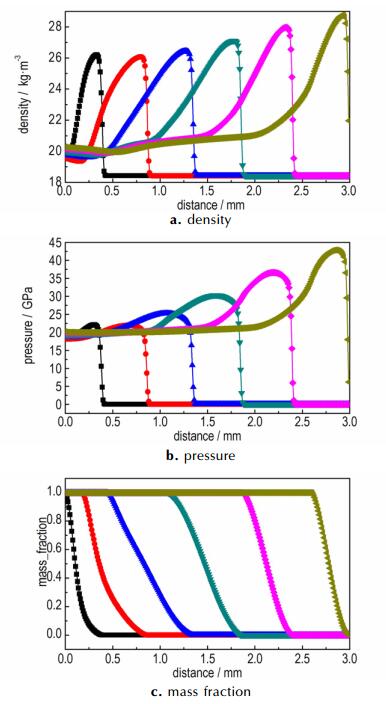
图 6为拐角沿内壁面3 mm距离内密度、压力和质量分数在不同时刻的分布曲线。从图 6可以看出0.50 μs时角点附近压力约为10 GPa, 密度为2.0×103 kg·m-3, 可以认为属于熄爆区域, 形成临时的“死区”, 此时前导冲击波与化学反应解耦, 冲击波能量主要用于波的膨胀, 因此引起后面化学反应变慢且反应区宽度变宽, 而随着前导冲击波远离拐角, 未反应炸药又重新开始反应, 爆轰波阵面沿内壁面向下传播并不断成长为稳定爆轰波。
|
图 6 90°拐角爆轰时物理量随时间变化曲线(t=0.50 μs到0.75 μs,Δt=0.05 μs) Fig.6 The change curves of physical quantity with time when detonation at the 90° corner(t=0.50 μs to 0.75 μs, Δt=0.05 μs) |
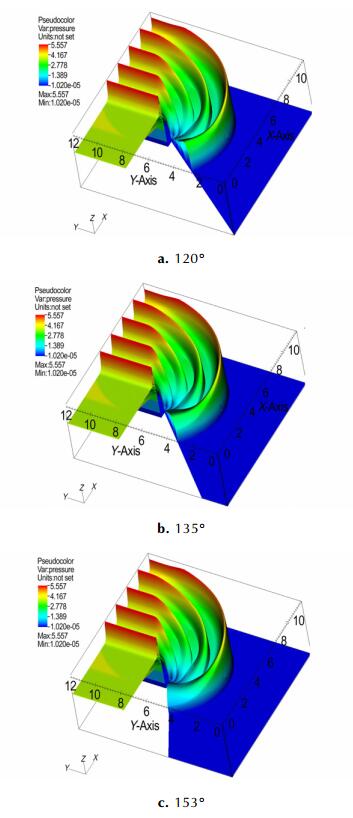
90°拐角情况下, “死区”内的炸药又重新加速反应, 内壁面附近发生二次起爆, 将拐角增大至120°、135°和153°, 图 7给出了不同时刻的压力分布, 由图 7可以发现三种角度下拐角附近首先压力持续下降, 135°情况下0.8 μs时拐角压力为1 GPa, 说明拐角角度的增大对爆轰波阵面产生了更大的稀疏作用, 且拐角下游区域的“死区”区域随着角度增大而变大; 而随着时间的演化, 熄爆区域压力最终又重新升高, 说明在拐角扩大到153°时仍没有形成永久的“死区”, 这与Banks[6]关于LX-17炸药的结论一致。
|
图 7 拐角绕射时压力变化(t=0.45 μs到1.15 μs, Δt=0.175 μs) Fig.7 The pressure change at corners diffraction(t=0.45 μs to 1.15 μs, Δt=0.175 μs) |
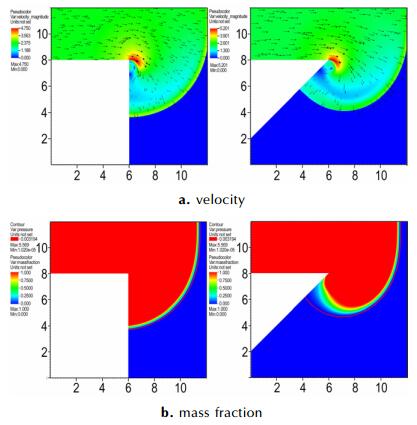
图 8a出了PBX9404炸药在90°和135°拐角速度对比, 由图 8a可知, 135°拐角附近区域发生明显的“涡流”, “涡流”周围的粒子围绕中心沿顺时针运动, 中心处的粒子速度接近0, 因此可以说明拐角较大时前导冲击波的能量主要用于涡流的运动, 因此化学反应将变慢, 且形成低压低密度区域。
|
图 8 90°拐角和135°拐角绕射时速度和产物质量分数对比(t=1.1 μs) Fig.8 Comparison of the velocity and the mass fraction of products when diffraction at 90° corner and 135° corner at t=1.1 μs |
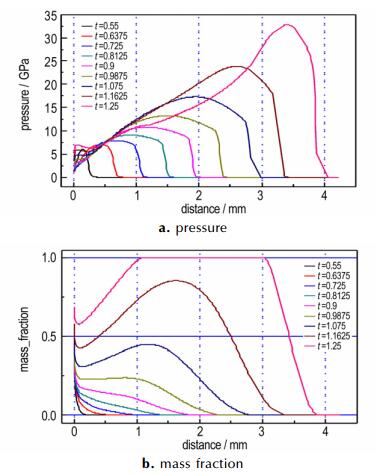
图 8b给出了90°和135°拐角爆轰产物质量分数对比, 其中红线代表前导冲击波波阵面, 由图 8b可知, 1.0 μs时, 135°拐角情况下前导冲击波与化学反应完全解耦, 爆轰熄爆。图 9为拐角内壁面区域的压力和质量分数随时间变化的曲线, 可以发现0.55 μs时拐角区域的炸药几乎没有反应, 随着侧向冲击波的传播, 到1.0 μs炸药开始缓慢反应, 但反应区域已完全滞后于压力波波阵面; 从1.075 μs到1.25 μs, 炸药反应开始加速。
|
图 9 135°拐角爆轰时压力和质量分数随时间变化曲线 Fig.9 The change curves of pressure and mass fraction with time when detonation at 135°corner |
从质量分数曲线(图 9b)可以发现, 产物质量分数在1.5 mm到2 mm最大, 说明炸药反应是在波阵面后的未反应炸药的局部开始反应, 并且反应是向两个方向进行, 这就是炸药爆轰的“回爆”现象, 沿着冲击波方向的反应能量会加速爆轰反应, 趋向于稳定爆轰, 而与冲击反向的会使压力出现扰动, 因此可以得到“死区”内炸药重新起爆的需要回爆波强度小于一定的诱导时间和诱导距离。Hill基于改进的圆筒实验[5]研究“死区”效应时, 定义了诱导时间, 结合能量释放时间来研究二次起爆过程, 基于该实验研究, 我们同样定义诱导时间Δti, 诱导时间为产物质量分数从0.5到1的所需时间, 而对应的距离为诱导距离Δli, 对于135°拐角的PBX9404炸药, 从图 9中可以发现, 靠近壁面的诱导时间约为0.2 μs, 诱导距离约为2 mm, 与Hill[5]的实验可以得到一致的结论。
6 结论构建了多介质混合爆轰模型, 采用点火增长模型描述炸药起爆、爆轰反应过程, 结合基于非结构网格的有限体积方法和爆轰反应区平衡迭代算法实现凝聚相炸药爆轰的数值模拟并验证了物理模型、数值方法和软件模块的正确性。基于数值模拟重点讨论和分析了不同拐角下的爆轰波的传播过程, 得到以下结论:
(1) 凝聚相炸药拐角爆轰过程中的拐角越大, 爆轰波衍射作用越明显, 衍射波波阵面与当地流场满足一定的关系。
(2) 拐角爆轰“死区”的形成原因是拐角的存在引入稀疏波并形成“涡流”, 导致化学反应与侧向爆轰波解耦, 拐角“死区”范围随着拐角增大而扩大。
(3) 定义了拐角爆轰过程的临界诱导距离, 死区内炸药能否重新起爆的关键是回爆波引起的炸药快速反应时间是否大于炸药的临界诱导时间, 如果回爆波作用时间大于拐角炸药作用时间, 则炸药能快速重新起爆。
此外, 本研究采用的点火增长模型是永久死区未能形成的原因之一, 后续工作会重点考虑拐角的作用, 研究不同反应模型对于死区的影响。
| [1] |
Tarver C M, Hallquist J O. Modeling Two-Dimensional Shock Initiation and Detonation Wave Phenomena in PBX 9404 and LX-17[C]//In: Short J M, Ed. The Proceedings of The 7th Symposium (International) on Detonation Annaplis MD, 1981. White Oak MD: Naval Weapons Center, 1981.
|
| [2] |
Tang P K, Forest C. Shock wave initiation of heterogeneous reactive solids[J].
Journal of Applied Physics., 1985, 57: 4323 DOI:10.1063/1.334591 |
| [3] |
Jia Quansheng, Liu Jupeng, Feng Changgen. Numerical Modelling for Turning Corner Effect of Detonation Wave and Convergent Wave Effect[C]//In: Zhang Guanren, Huang Shihui Ed. The Proceedings of The 2nd International Symposium on Intense Dynamic Loading and Its Effect. Chengdu China: Sichuan University Press, 1992, 137.
|
| [4] |
于川, 赵同虎, 孙承纬. 四种炸药爆轰波绕射数值模拟研究[J].
爆炸与冲击, 1998, 18(1): 35-41. YU Cuan, ZHAO Tong-hu, SUN Cheng-wei. Numerical simulation on diffraction of detonation waves in four explosvies[J]. Explosion and Shock Waves, 1998, 18(1): 35-41. |
| [5] |
Hill L G. Is the detonation "Dead Zone" really dead?[C]//Proceedings of the Combustion Institute, 2015, 35: 2041-2049.
|
| [6] |
Banks J W, Henshaw W D, Schwendeman, et al. A study of detonation propagation and diffraction with compliant confinement[J].
Combustion Theory and Modeling, 2008, 12(4): 769-808. DOI:10.1080/13647830802123564 |
| [7] |
Banks J W, Schwendeman D W, Kapila A K, et al. A high-resolution Godunov method for compressible multi-material flow on overlapping grids[J].
Journal of Computational Physics, 2007, 223: 262-297. DOI:10.1016/j.jcp.2006.09.014 |
| [8] |
Tarver C, Urtiew P. Theory and modeling of liquid explosive detonation[J].
J Energ Mater, 2010, 28(4): 299-317. DOI:10.1080/07370651003789317 |
| [9] |
Michael L, Nikiforakis N. A hybrid formulation for the numerical simulation of condensed phase explosives[J].
Journal of Computational Physics, 2016, 316: 193-217. DOI:10.1016/j.jcp.2016.04.017 |
| [10] |
Lee E, Tarver C. Phenomenological model of shock initiation in heterogeneous explosives[J].
Phys Fluids, 1980, 23: 2362 DOI:10.1063/1.862940 |
| [11] |
Toro E.
Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction[M]. Springer, 2009.
|
| [12] |
Press W, S Teukolsky, Vetterling W, et al.
Numerical recipes, in: The Art of Scientific Computing[M]. 3rd edition, Cambridge University Press, 2007.
|




