1  引言

Schlieren 成像技术是利用媒质光学性质的不均匀对光衍射过程产生相位调制来实现的光学成像技术，由于 它光路系统简单，是一种研究透明介质中光学不均匀性很有效的方法，比如空气、水、玻璃等透明媒质中我们看不见的光学不均匀性。因此， Schlieren 成像技术是一种有广泛应用的成像技术 [1] 。

Schlie ren 成像的研究可追溯至 Robert Hooke （ 1635-1703 ）。他首先利用 Schlieren 系统观察蜡烛燃烧引起的热空气扰动 [2] 。二战后期，大型超音速风洞和高速飞行器的研究，促进了 Schlieren 技术的发展，使它成为研究大空间中冲击波的有效手段。 1974 年， Merzkirch 对可压缩流场测试研究中应用的 Schlieren 方法进行了分类，并把 Schlieren 系统中有光干涉效应的，像光栅干涉、棱镜干涉及 Moire 条纹干涉等都称之为 Schlieren 技术 [3] 。现在，各种 Schlieren 光学系统已经广泛应用于：流场测量 [4] ；液体混合过程 [5] ；燃烧和温度场测量 [6-7] ；冲击波 [2 , 8] ；等离子放电 [9] 等的研究。

当声波在媒质中传播时，同样会引起媒质光折射率的改变而对光波产生相位的调制，因此，可以利用 Schlieren 技术对声的传播和声场进行成像研究 [10-16] 。由于 Schlieren 技术是一种光学成像技术，具有非侵入和快速成像的特点，由于它对声场不产生任何扰动，所以它具有精确定量检测声场的优势。同时，它的瞬态成像可以用于声场的可视化研究，使声与媒质之间相互作用的一些复杂的物理过程可以直观地显示和研究。

将传统的 Schlieren 技术与现代的激光技术和髙速摄影技术相结合，我们建立了可进行瞬态成像和定量研究的 Schlieren 成像系统。本文将结合光传播理论和我们近期的实验结果，对 Schlieren 技术在声场定量检测和声场可视化方面的应用作些简单介绍。

2  Schlieren 系统

2.1 原理

4 f ( 焦距 ) 的 Schlieren 光学 成像 系统 如 图 1 所示。它由两个焦距分别为 f 2 和 f 3 共焦 的透镜系统共焦组成，系统有三个焦平 面：物平面 (OP ： Object Plane) 、变换平面 (SFP ： Schlier en Filtering Plane) 和像平面 (IP ： Image Plane) 。每一个透镜系统是由一透镜和它前后两个自由传播空间构成。所以，如果把这个透镜光学系统看成光学 线性系统，物平面上的光信号作为系统的输入，只要已知光波在自由空间的传递函数和透镜的透 过率 函数，就可以确定透镜系统的传递函数而得到系统的输出。这样， Schlieren 成像系统中物平面和像平面上光的复振幅之间的关系就确定了。因此可以利用二维光学 Fourier 变换对 Schlieren 系统进行理论分析。

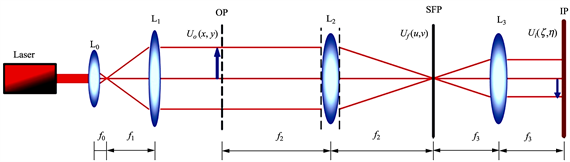
图 1 Schlieren 光学 成像系统

由二维光学 Fourier 变换理论知 [17] ， 在傍轴近似下 ， 光信号 U o ( x o ,y o ) 在自由空间中沿 z 方向传播距离 z 后的光信号 U ( x,y ) ， 可表示为 ：

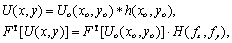                            (1)

式中 F T [ U ] 是函数 U 的 Fourier 变换，传递函数 h ( x , y ) 和响应函数 H ( f x , f y ) 为：

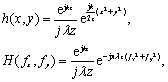                            ( 1a )

其中： k   =   2π/ λ 为光波波数， λ 是光波波长， f x 和 f y 是空间频率 :

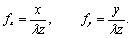                            (1b)

对于中心厚度 Δ 0 、焦距 f 的薄 透镜 ，它的透过率 t I 可表示为：

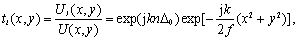
(2)

式中： n 是透镜材料的折射率， U ( x,y ) 、 U I ( x,y ) 分别是透镜前、后的输入和输出平面光波。由于 exp( j kn Δ 0 ) 是恒定的相移，可以略去，所以透镜的透

过率可直接表示为：

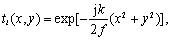                            (3)

它表明透镜在光学系统中起了相位调制的作用。

对于图 1 所示的透镜系统，它的物平面在 L 2 的前焦平面 OP 上，而输出平面是后焦平面 SFP ，利用式 (1) 和 (3) ，可以得到：

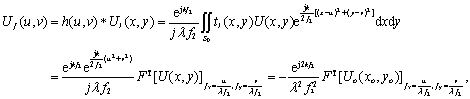                            ( 4 )

即一个透镜的前后焦平面上的光信号是严格 Fourier 变换关系。

同理，对于 L 3 透镜系统有：

                            (5)

这样，利用式 (4) 和 (5) ，可以得到由共焦的 L 2 和 L 3 透镜系统组成的 Schlieren 光学系统，它像平面上的光信号与物平面上的输入信号之间的关系：

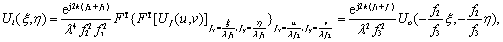                            (6)

 

式 (6) 表明，共焦的 4 f S chlieren 系统 得到的是一个放大倍数为 f 3 /f 2 的倒立像。

由于系统共焦面 SFP 上的光信号 U f ( u,v ) 是输入信号 U o ( x o , y o ) 的 Fourier 变换，即是信号 U o ( x o ,y o ) 的空间频谱，所以把这平面称为变换平面。在该平面作空间滤波可以方便地进行光信号的处理 ， 这是 Schlieren 系统成像的一个重要特点。而由于透镜的焦距是有限长的，所以 Schlieren 系统的放大倍数不髙，这是成像技术的一个不足之处。

2.2 实验

为验证 Schlieren 成像理论，建立了 He-Ne 激光的 Schlieren 成像系统。波长为 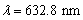的激光束，经扩束镜 L 0 ( 焦距 f 0   =   10   mm) 、准直透镜 L 1 （ f 1   =   200   mm ）扩束准直后 , 形成直径为 35.0   mm 的平行光束入射到物面上。变换透镜 L 2 与成像透镜 L 3 的焦距分别为 f 2   =   500   mm 和 f 3   =   300   mm 。所以，系统的放大倍数为 3/5 。

利用 iStar ICCD 高速摄影机记录光信号。是将一片网孔尺寸为 320.2   μm   ×   319.8   μm 涂黑的金属丝网放在物平面上，在变换平面和像平面上得到的光像如图 2 ( b) 和 ( c) 所示。图 2 ( b) 得到的是激光束通过网格形成的等间距的衍射光斑，而图 2 ( c) 是网格的像，网孔像的尺寸为 192.1   μm   ×   192.1   μm ， 由像及放大倍数 3/5 可以推算出成像网格的尺寸是 320.2   μm   × 320.2   μm, 与实物尺寸完全一致。

图 3 在 铝膜上用激光烧蚀刻上数字 “ 5 ” 在 Schlieren 系统的成像 结果。结果再一次证实系统得到的是真实反映物体的倒立像。

图 2   金属网的 Schlieren 成像

图 3 铝膜上蚀刻的数字“ 5 ”的 Schlieren 成像

3  平面波 声场的 Schli eren 成像

3.1   平面波声场的成像

图 4 是 4 f 的 Schlieren 声成像 和 定量测量系统，一个透光的水槽放在平行光束的光路中，它的后壁面位于透镜 L 2 的前焦面而成为光学成像系统的物平面 OP 。

当声压为 p   =   p a sin( ω a t - k a x ) 的平面声波沿 x 方向在水中传播时，它对沿 z 方向传播的平面光波

A exp( ωt - k z ) 的相位产生调制，在物平面上的光信号可表示为：

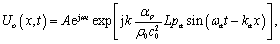              (7)

式中： A 为光波振幅， ω 和 ω a 分别是 为光波和声波的圆频率 ， k 和 k a 分别是为光波和声波的波数， ρ 0 和 c 0 分别是 水的 密度和声速， α p 是水的绝热压光系数，它与媒质的折射率有关 [ 18] ：

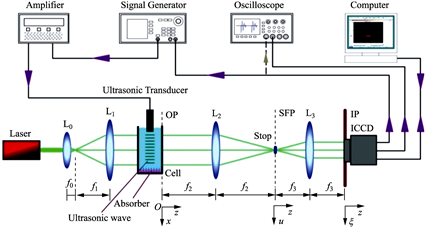
图 4  Schlieren 声成像系统示意图

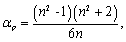                            ( 7a )

当光波波长为 632.8   nm 时，水的压光系数为 α p   =   0.323 。而 L 是声光相互作用的长度。

由式 (4) ， 可以得到在 SFP 变换平面上的光信号：

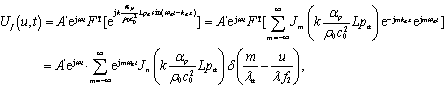                            (8)

上式中利用了公式：

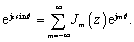
式 (8 ) 表明，在变换平面上得到的将是一列沿 u 方向分布的离散的衍射光斑，相邻衍射光 斑 之间的距离为：

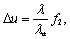                            ( 8a )

式中 λ 是光波波长， λ a 是声波波长。所以，为了能在空间区分各级衍射光斑，在 λ 和 f 2 确定的系统中，成像的声场频率不能太低。而各级衍射光强为：

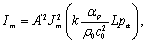                            (8b)

它 们都是与声压振幅有关的同一个宗量 z 的函数 ：

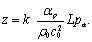                            ( 8c )

因此，可以通过测量各级衍射光斑的光强来实验确定平面声波的声压。

在变换平面用光阑遮掉其他衍射光斑，只让零级衍射光通过而成像，这时，像面 IP 上光复振幅 U i ( ξ,t ) 是变换平面上光复振幅 U f ( u , t ) 的零级衍射光分量的 Fourier 变换， 对 (8) 式中的 m   =   0 的分量作付氏变换， 得到在像平面上的光信号为：

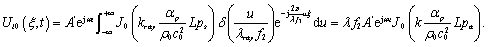                            (9)

结果表明零级衍射光斑形成的是一个无反差的亮场像 ， 所以在 Schlieren 成像中 ， 通常都把零级衍射光斑挡掉 ， 进行暗场成像。

若只让变换面上的一级衍射光通过成像，对 (8 ) 式中的 m   =   1 的分量作 Fourier 变换，在像平面上的光信号为：

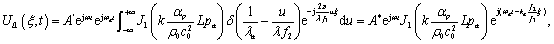                            ( 9a )

即光信号是放大了 f 3 /f 2 倍的声场像。像面上的光强分布为：

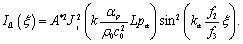                            (9b)

像平面上光像的相邻亮（暗）条纹之间的距离 ， 是声波波长的 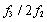倍 ：

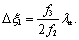                            ( 9c )

当只让第 m 级衍射光斑通过光阑成像，在像平面上的光信号 U i m 和光强 I im 分别是 :

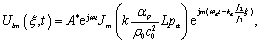                            (9d)

                            (9e)

式 (9e) 表明，像平面上的光强与 J m 2 ( z ) 成正比，而像的亮暗条纹变密，相邻亮条纹的间距为：

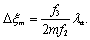                            ( 9f )

因此，通过变换平面上作适当的空间滤波，可以得到不同光强和分布的声场像。

3.2   换能器校准

活 塞换能器辐射平面波声场的电压发射响应 S v 为：

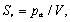                            (10)

式中 V 是施加在换能器上的交流电压， p a 是平面波的声压。将上式代入式 ( 8 c ) ，得到宗量 z 与 S v 的关系：

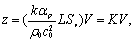                            (11)

式中：

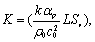                            ( 11a )

是由系统参数决定的物理量。

利用 贝塞尔函数 J m ( z ) 与它参量 z 之间的关系式 ， 以及由式 (8b) 的各级衍射光强 I m 与贝塞尔函数 J 2 m ( z ) 成正比，得到参量 z 与光强 I m 的关系：

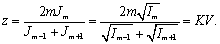                            (1 2)

因此，当系统参量 λ, ρ 0 , α p , c 0 和 L 确定后，通过测量相邻三级衍射级光强 I m ，就可得到参量 z 与电压 V 之间的关系，进而确定系数 K 而实现对换能器发射响应的校准。

图 5 是泛美 A314S ， 1.0   MHz 换能器辐射的声场像以及在变换平面上相应的衍射光斑像 。通过测量不同发射电压下相邻的三级衍射光斑光强，得到相应的宗量 z ( 图 6) ，从而得到 z - V 直线的斜率 K   =   0.026 8±0.0003 ( 高斯分布， 95% 置信限，相关系数为 0.9954) 。

由实验测定水的声速 c 0   =   (1484±4) m/s ，声光作用长度 L   =   11.8   mm ，以及已知 λ   =   632.8   nm ， ρ 0   =   1.0×10 3   kg/m 3 ， α p   =   0.323 ，由式 ( 11a ) 可以得到换能器的电压发射响应：

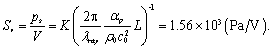              ( 12 a )

利用发射响应就可以确定在不同激励电压下平面波声压的大小。

图 5  不同激励电压下 1.0 MHz 换能器辐射的声场像以及在变换平面上相应的衍射光斑像

 

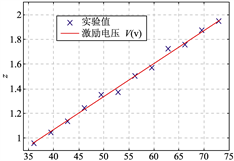
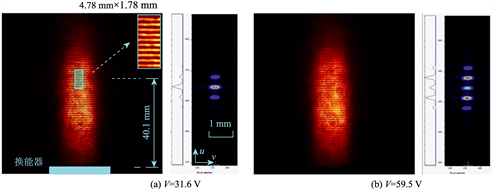
图 6   宗量 z 与换能器激励电压 V 的实验曲线

为了验证 Schlieren 方法校准换能器技术的可靠性，将同一个换能器用 超声辐射力法 进行了测量。超声辐射力法釆用的是 ULTRASONIC POWER METER Model UPM-DT-1 & 10 AV 系统，实验时气温 25   ℃，湿度 44% ，水温 24   ℃， 液体 是未除气的自来水。两种方法的实验结果如图 7 所示。两种方法在较大激励电压下有约 7 ％的偏差，这可能是由

于系统误差，以及超声辐射力校准时没用去气水等原因造成。

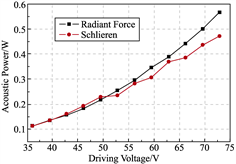
图 7  Schlieren 方法和超声辐射力法校准换能器结果比较

图 8 ( a) 是凹柱面声透镜线聚焦换能器声场的有限元计算 结果 ，而图 8 ( b) 是它的 Schlieren 像。结果都表明在它焦斑处的声场可认为是一个平面波声场。因此，可以利用 Schlieren 方法对线聚焦超声换能器焦斑上声压进行测量。

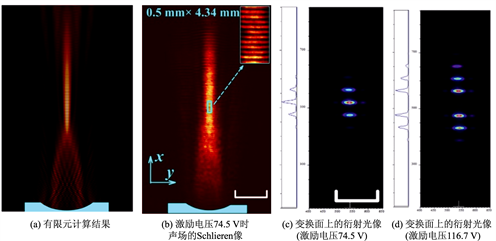
图 8   凹柱面声透镜换能器不同激励电压下的辐射声场像和衍射光斑分布， f a   =   1.6   MHz

测量通过声焦斑区域的激光在变换平面上相邻 三级 衍射光斑的光强 ，可以得到宗量 z 随换能器激励电压 V 变化的线性关系，得到拟合直线的斜率 为 k   =   0.02519±0.00082 （置信限 95% ，均方差为 0.998 ， 图 9 ）。再利用实测的声光作用长度 L   =   10.3   mm 和水的声速 c 0   =   1486   m/s ，可以得到该线聚焦换能器的电压发射响应为：

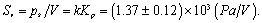
采用移相锁相积分法 , 可以对换能器 辐射声场的聚焦过程 进行动态 Schlieren 成像。图 10 是频率

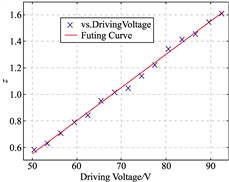
图 9   凹柱面声透镜换能器宗量 z 与
换能器激励电压 V 的实验曲线

1.60   MHz 、 凹柱面声透镜线聚焦超声换能器 ，在 74.49   V 的单脉冲正弦信号激励下不同时刻的辐射声场。声像的曝光时间 20   ns ，曝光频率 1.00   kHz 。 Schlieren 像形象地显示了声波的聚焦过程。

 

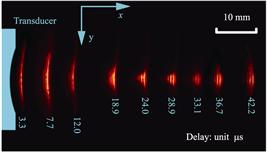
图 10 凹柱面声透镜线聚焦超声换能器辐射
声场聚焦过程的 Schlieren 像

3.3 固 - 液界面的声场成像

平面声波从流体中以入射角 θ i 斜入射到液固界面时，会产生声的反射和折射。当固体的纵波声速 c L 、横波声速 c T 和 Rayleigh 波的声速 c R 大于流体的 声速 c 0 时，随着入射角 θ i 的增大，会发生临界折射现象。由 Snell 定律可确定相应的纵波、横波、 Rayleigh 波临界角 θ L 、 θ T 和 θ R ：

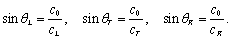                            ( 13 )

对于水 -K 9 玻璃 界面 ， K 9 玻璃 的纵波、横波波速分别为： c L   =   ( 5796 ± 13 ) m/s ， c T   =   ( 3393 ± 4 ) m/s ；广义 Rayleigh 波波速 c R ’   =   (3125 - i 105.9) m/s ， K 9 玻璃的 尺寸： 51.56   mm 89.60   mm 51.56   mm 。而水中声速 c 0   =   1485   m/s 。所以，相应的临界角为：

，

，

              .

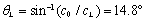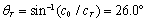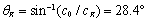图 11 是 5MHz 的有限束宽的平面声波从水入射到 K 9 玻璃界面 声场的 Schlieren 像 。实验结果表明：反射声场是由正常的镜面反射波与固体中临界折射声波产生的泄漏波组成。由于沿界面传播的折射波是衰減的凋落波，传播一段距离后就衰减了，于是在有限束宽的平面波入射时就出现了一定束宽的正常反射 波束 与有平移的泄漏波束相叠加的反射声场。如果两束波重叠处相位相同，振幅就增大，相位相反就減弱。

从图 11(a) 和 (b) 可以看到，当入射角在临界角 θ L 和 θ T 之间时，除了镜面反射声束 A 外，同样存在非镜面反射声束 B 。而在临界角 θ R 附近，由图 11 ( d) 可知，除了较强的 泄漏 瑞利波束 B 外 [19] ，还有较弱的泄漏波束 C 和 D 。

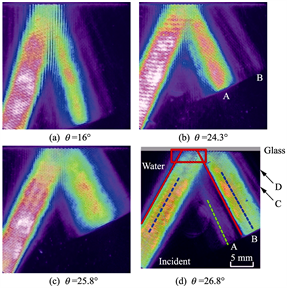
图 11  5 MHz 的有限束宽平面声波从水入射到
K 9 玻璃界面声场的 Schlieren 像

当有限束宽平面波斜入射到一块 浸 没在 水 中的板时，由正常反射和透射声波与泄漏 Lamb 波相叠加，也会出现异常的非镜面反射声场 [20] 。图 12 是 5   MHz 平面声波束斜入射到厚度为 2.23   mm 、浸没在水中玻璃板时声场的 Schlieren 像。由实验结果可以清楚看到，在液体中除了反射和透射声束外，还有泄漏 Lamb 波 B( 图 12 ( b ) ) 。

图 12  5.00 MHz 声波以 入射角 22.7° 入射到
浸水玻璃板界面后液体中的声场

Schlieren 成像也可应用于 观测 粘接 界面缺陷的 观测。 图 13 是相同尺寸的玻璃和有机玻璃板的 粘接 试样，在 粘接 界面上贴上 宽 5   mm ，厚 30   μm 的聚 薄膜。 5   MHz 的声波以 16.3° 入射 。当透入玻璃 的声波与缺陷作用时，反射回波增强，而透射声波減弱。当声束离开缺陷区时，透射声波迅速增强。

 

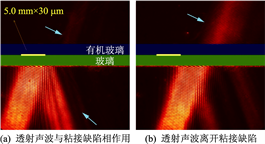
图 13   界面有缺陷的 粘接 板在水中的
声场 Schlieren 像（入射角 16.3° ）

4  结论

基于二维光学 Fourier 分析， 4 f 的 Schlieren 光学成像系统本身就是一个 Fourier 变换处理器，在像平面上得到的是放大倍数为 f 2 / f 3 的倒置像。我们将 现代的激光技术和 ICCD 高速摄影技术与 Schlieren 技术相结合，自行建立了一个以开展声压定量测量和声传播可视化为目标的 Schlieren 成像系统。利用成像系统中变换平面上衍射光斑强度与平面波声压的理论关系，进行了平面活塞换能器和线聚焦换能器的电压发射响应的光学校准，并与超声幅射力法相比较，两者最大偏差在 7 % 左右。开 展了聚焦声场，固 - 液界面和浸液板界面声场的动态 液 - 固界面的异常非镜面反射声场，浸液板幅射的泄漏 Lame 波声场等，表明 Schlieren 成像技术对于揭示复杂的声传播现象的本质是十分有效的。然而， Schlieren 成像的放大倍数较低，以及成像的声波频率不能太低等缺点，还有待于进一步研究克服。 Schlieren 技术也可用于声子晶子中声传播的研究，有关内容将另外拟文介绍。

参　考　文　献

[1]   SETTLES G S. Schlieren and shadowgraph techniques: visualizing phenomena in transparent media [M]. NewYork : Springer , 2001.

[2]   NEUMANN T , ERMERT H. Schlieren visualization of ultrasonic wave fields with high spatial resolution[J]. Ultrasonics , 2006 , 44 : 1561-1566.

[3]   MERZKIRCH W. Flow Visualization[M]. New York : Academic Press , 1974.

[4]   SATHEESH K , JAGADEESH G , REDDY K. High speed schlieren facility for visualization of flow fields in hypersonic shock tunnels[J]. Current Science , 2007 , 92 : 56-40.

[5]   SEMWAL K , RANJAN R , PANIGRAHI P , et al . Color schlieren deflectometry study of jet mixing : effect of buoyancy and perforation [J]. Heat and Mass Transfer , 2012 , 48(3) : 541-554.

[6]   安新亮 , 何旭 , 王丽雯 , 等 . 应用高速纹影法对汽油机燃烧过程的研究 [J]. 内燃机工程 , 2007 , 28 : 1-5.

[7]   MARTNEZ-GONZLEZ A , GUERRERO-VIRAMONTES J , MORENO-HERNNDEZ D. Temperature and velocity measurement fields of fluids using a schlieren system[J]. Applied optics , 2012 , 51 : 3519-3525.

[8]   WILLERT C , MITCHELl D , SORIA J. Megahertz Schlieren Imaging of Shock Structure and Sound Waves in Under-Expanded[J]. Impinging Jets , 2010 : 1-3 .

[9]   BOTT S C , H AAS D M , U EDA U , et al . High-Resolution Laser Schlieren Imaging of Coronal Plasma Evolution in 80-kA X-Pinches[J]. IEEE Transactions on Plasma Science , 2008 , 36(4) : 1274-1275.

[10]             CHINNERY P A , HUMPHREY V F , BECKETT C. The schlieren image of two-dimensional ultrasonic fields and cavity resonances[J]. The Journal of the Acoustical Society of America , 1997 , 101(1) : 250-256.

[11]             UNVERZAGT C , OLFERT S , HENNING B. A new method of spatial filtering for Schlieren visualization of ultrasound wave fields[J]. Physics Procedia , 2010 , 3 : 935-942.

[12]             KUDO N , SANBONMATSU Y , SHIMIZU K. Microscopic visualization of high-frequency ultrasound fields using a new method of Schlieren photography [C]. 2010 IEEE International Ultrasonics Symposium Proceedings , 2010 : 829-832.

[13]             ZHU Guozhen , ZHU Xifu , LIU Liang. Examination on existence of slow wave in fluid saturated porous medium with the optical method[J]. Chinese. Journal of Acoustics , 1999 , 18(4) : 304-310.

[14]             ZHU Guozhen , LIU Liang , FU Deyong. Reflected beam displacements of a slightly divergent ultrasonic Gaussian beam on a water-glass interface near rayleigh angle incidence[J]. Chin. Phys. Lett , 1999 , 16(11) : 819-821.

[15]             ZHU Guozhen , LU Kean , FU Deyong , et al. Experiments on two kinds of threshold of the acoustic pressure gradient for schlieren system[J]. Measurement Science and Technology , 2002 , 13(4) : 483 - 487.

[16]             ZHU Guozhen , SUN Yao , FU Deyong. Visual-Width of an Ultrasonic Gaussian Beam on the Schlieren Photograph and Explanation to the Nonspecularly Reflected Sound Field[J]. Chinse Physics Letter , 2004 , 21(1) : 341-344.

[17]             J W 顾德门著 , 詹达三 , 董经武 , 顾本源译 .  Fourier 光学导论 [M] , 北京 : 科学出版社 , 1979.

[18]             SCRUBY C B , DRAIN L E.  Laser ultrasonics : techniques and applications[M]. Philadelphia and New York : Adam Hilger Bristol 1990.

[19]             诸国桢 , 刘亮 , 傅德永 . 液 - 固界面上非镜面反射的波束位移的实验研究 [J]. 中国科学 (A 辑 ) , 2000 , 30(7) : 653-660.

[20]             J L 罗斯著 , 何存富 , 吴斌 , 王秀彦译 . 固体中的超声波 [M] . 北京 : 科学出版社 , 200 4 : 104-105.