2. 大连理工大学工程力学系,辽宁 大连 116024;
3. 大连理工大学,辽宁 大连 116024
2. Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China;
3. Dalian University of Technology, Dalian 116024, China
滑移爆轰作用下飞板运动规律的研究是爆炸焊接理论研究中十分重要的问题。在二维滑移爆轰驱动平板的过程中,深入研究飞板的飞行姿态对于优化焊接工艺中的各种参数和改善复合板的焊接质量,提高复合率具有重要意义[1]。因此,自从爆炸焊接理论发现以来,国内外的大量学者都对此进行了大量的研究,先后提出了Gurney、Aziz的一维运动模型和Richter的二维模型[2];我国学者邵丙璜[2]利用了Prandtl-Meyer理论来描述爆炸产物的稀疏作用,得到了比较严格二维的理论公式,基于邵丙璜的理论,郭佑雄[1]又提出了双P-M法,王飞[3]等人对飞板的运动进行了特征线差分计算,这三种方法都能较好地计算飞板的运动状态,但是在计算爆轰压力时都采用了形式非常简单的多方方程,不能非常准确地描述炸药的爆轰压力,所以具有一定的局限性。目前,采用有限元软件LS-DYNA对滑移爆轰的过程进行数值模拟很广泛,通过数值计算得到飞板的飞行参数,但是利用有限元软件计算的过程中涉及到许多问题,比如有限元模型的建立,材料参数的选择,算法的选择,人工粘性的控制,沙漏控制等,这些参数对于数值模拟有着非常大的影响。所以利用LS-DYNA准确地计算滑移爆轰驱动平板的飞行姿态是非常困难的。
特征线方法是计算二维超声速流的方法之一,由于滑移爆轰涉及到可压缩流场的问题,所以特征线法常常应用于计算滑移爆轰中飞板的运动姿态。特征线方法的基本思想就是通过引入特征面(或特征方向)来减少独立变量的个数,把描述飞板运动的偏微分方程转化为常微分方程。这种方法物理概念和数学处理过程清晰[4],因此一直受到重视。为了准确地计算滑移爆轰中飞板的飞行规律,我们采用了特征线的差分法处理了流场,计算中采用了能更加准确描述爆轰产物压力的JWL等熵方程取代了形式非常简单的多方方程,更加准确地计算飞板的飞行参数。采用简单弱爆轰假设,对于稳定的滑移驱动飞板运动,将坐标系置于爆轰波头上,爆轰产物的流场就是定常的,按照二维可压缩流处理爆轰产物的流动,研究了通用状态方程的特征线差分方法,利用通用状态方程和多方方程的特征线法对爆轰产物流场进行数值计算,并分别对这两种计算方法得到的结果进行了比较研究。
2 二维定常流特征线相容关系由二维可压缩定常等熵无旋流的特征线理论[5]可得到,马赫线(即特征线)和特征线上的相容方程分别为(1)和(2),由于方程(1)和(2)与气流的物质、物态方程无关,所以是一种通用物态方程的特征线关系。
| $ {{\left( \frac{\text{d}y}{\text{d}x} \right)}_{\text{I, II}}}=\text{tg}(\theta \pm \alpha ) $ | (1) |
| $ {{(\text{d}\theta )}_{\text{I, II}}}=\pm \sqrt{{{M}^{2}}-1}\frac{\text{d}q}{q} $ | (2) |
其中, Ⅰ, Ⅱ分别表示第一、第二族特征线方程, M是马赫数, θ是流速q与流动方向的角, α=arcsin(1/M)。对于定常可压缩流,可用热焓i和流速q关系写出其伯努利(Bernouli)方程:
| $ i+\frac{1}{2}{{q}^{2}}={{i}_{0}} $ | (3) |
其中, 热焓i=e+pτ, 比容τ=1/ρ, e为比内能, p为爆轰压力;i0为总焓;q2=u2+v2,u和v分别表示流速的水平分量和竖直分量。对于满足不同状态方程的爆轰气体,其等熵方程与状态方程也不尽相同,下面就分别对满足不同等熵方程的气体求其特征线方程。
2.1 多方方程对于满足多方状态方程的爆轰气体,它的等熵方程和状态方程是相同的,李晓杰[6]已推导了多方气体的特征线相容关系:
| $ \left\{ \begin{align} &\theta \pm v\left( M \right)={{R}_{\text{I, II}}}~ \\ &v\left( M \right)=\sqrt{\frac{\gamma +1}{\gamma-1}}\text{arctg}\left[\sqrt{\frac{\gamma-1}{\gamma +1}({{M}^{2}}-1)} \right]-\text{arctg}\sqrt{{{M}^{2}}-1} \\ \end{align} \right. $ | (4) |
其中, RⅠ和RⅡ是常数,分别称为第一黎曼不变量和第二黎曼不变量, v(M)是Prandtl-Meyer函数,M是马赫数,γ是多方指数。
对于满足多方气体爆轰产物的内部和飞板的边界差分在文献[3, 6]已做了说明,在此不再赘述。
2.2 JWL等熵方程对于一般的凝聚态炸药,采用JWL状态方程更能准确地描述爆轰产物的状态,因此,利用JWL等熵方程推导和爆轰气体的特征线相容关系和爆轰产物的内部差分和飞板的边界差分。JWL等熵方程[7]为:
| $ \begin{align} &{{p}_{\text{s}}}=A{{\text{e}}^{-{{R}_{1}}V}}+B{{\text{e}}^{-{{R}_{2}}V}}+~\frac{C}{{{V}^{\omega +1}}} \\ &{{e}_{\text{s}}}=~\frac{A}{{{R}_{1}}}{{\text{e}}^{-{{R}_{1}}V}}+~\frac{B}{{{R}_{2}}}{{\text{e}}^{-{{R}_{2}}V}}+\frac{C}{\omega {{V}^{\omega }}} \\ \end{align} $ | (5) |
其中, A, B, C, R1, R2, ω为炸药的状态常数,由圆筒实验得到,ps, es分别为等熵压力和内能,V=τ/τ0是相对体积,τ为比容。
对式(3)求导,并利用qdq=-di以得到:
| $ \text{d}q/q=\text{d}(\text{ln}\sqrt{~{{i}_{0}}-i}) $ | (6) |
由M2=q2/c2=2(i0-i)/c2, c为声速,c2=dp/ρ,和式(2)推导可以得到下面的关系:
| $ \text{d}v\left( M \right)=-\frac{1}{c}\sqrt{2\left( {{i}_{0}}-i \right)-{{c}^{2}}}~\text{d}(\text{ln}\sqrt{{{i}_{0}}-i}) $ | (7) |
其中, q为流速,i0为滞止焓,i为热焓,v(M)函数是关于马赫数M的函数,M又是焓i的单值函数,而焓i是密度ρ的单值函数,所以通过转化积分式(7)为密度ρ的函数进行数值积分得到密度ρ为自变量的表达式:
| $ \begin{align} &\text{d}v\left( \rho \right)=\text{ } \\ &\frac{1}{2}\sqrt{\frac{2\left[{{i}_{0}}-i\left( \rho \right) \right]-c{{\left( \rho \right)}^{2}}}{c{{\left( \rho \right)}^{2}}}}\frac{{{f}_{1}}\left( \rho \right)+{{f}_{2}}\left( \rho \right)+{{f}_{3}}\left( \rho \right)}{{{i}_{0}}-i\left( \rho \right)}\text{d}\rho \\ \end{align} $ | (8) |
其中, f1(ρ)=de/dρ,f2(ρ)=τdp/dρ, f3(ρ)=-p/ρ2, 可以由JWL等熵方程(4)得到。
联立式(4)、(6)、(7)和(8)得到JWL等熵方程的特征线相容关系:
| $ \left\{ \begin{align} &\theta \pm v\left( \rho \right)={{R}_{\text{I, II}}}~ \\ &\text{d}v(\rho )=\frac{1}{2}\sqrt{\frac{2[{{i}_{0}}-i\left( \rho \right)]-c{{\left( \rho \right)}^{2}}}{c{{\left( \rho \right)}^{2}}}}\frac{{{f}_{1}}\left( \rho \right)+{{f}_{2}}\left( \rho \right)+{{f}_{3}}\left( \rho \right)}{{{i}_{0}}-i\left( \rho \right)}\text{d}\rho \\ \end{align} \right. $ | (9) |
其中, RⅠ和RⅡ是常数,分别称为第一黎曼不变量和第二黎曼不变量, v (ρ)就是由Prandtl-Meyer函数转化成密度ρ的函数。
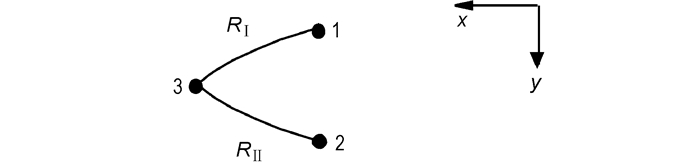
3 二维定常流特征线差分法 3.1 爆轰产物内部差分将通用状态方程的特征线相容关系(1)离散成差分的格式。如图 1,将第一族特征线RⅠ由已知点1和未知点3离散得出:
| $ \left. \begin{align} &({{x}_{3}}-{{x}_{1}})/\left( {{y}_{3}}-{{y}_{1}} \right)={{k}_{1}}~ \\ &{{\theta }_{3}}-{{\theta }_{1}}=v\left( {{\rho }_{3}} \right)-v({{\rho }_{1}}) \\ \end{align} \right\} $ | (10) |
|
图 1 爆轰产物中差分示意图 Fig.1 Scheme of differences in detonation |
其中, k1=[cot(θ1+α1)+cot(θ3+α3)]/2。
将第二族特征线RⅡ离散得到
| $ \left. \begin{align} &\left( {{x}_{3}}-{{x}_{2}} \right)/\left( {{y}_{3}}-{{y}_{2}} \right)={{k}_{2}}~ \\ &{{\theta }_{3}}-{{\theta }_{2}}=v\left( {{\rho }_{3}} \right)-v\left( {{\rho }_{2}} \right) \\ \end{align} \right\} $ | (11) |
其中, k2=[cot(θ2-α2)+cot(θ3-α3)]/2。
联立式(10)和(11),并利用马赫数和Prandtl-Meyer的关系,得到如下的解:
| $ \left. \begin{align} &{{\theta }_{3}}=\left[v\left( {{\rho }_{2}} \right)-v\left( {{\rho }_{1}} \right) \right]/2+\left( {{\theta }_{1}}+{{\theta }_{2}} \right)/2\text{ } \\ &{{\rho }_{3}}={{v}^{-1}}\left[{{\theta }_{3}}-{{\theta }_{1}}+v\left( {{\rho }_{1}} \right) \right]\text{ } \\ &{{i}_{3}}=e\left( {{\rho }_{3}} \right)+p\left( {{\rho }_{3}} \right){{\tau }_{3}}~ \\ &{{M}_{3}}=\text{ }\sqrt{2\left( {{i}_{0}}-{{i}_{3}} \right)/c_{3}^{2}} \\ &{{\alpha }_{3}}=\text{arcsin}\left( 1/{{M}_{3}} \right)\text{ } \\ &{{y}_{3}}=\left( {{x}_{2}}-{{x}_{1}}+{{k}_{1}}{{y}_{1}}-{{k}_{2}}{{y}_{2}} \right)/\left( {{k}_{1}}-{{k}_{2}} \right)\text{ } \\ &{{x}_{3}}={{x}_{1}}+{{k}_{1}}({{y}_{3}}-{{y}_{1}}) \\ \end{align} \right\} $ | (12) |
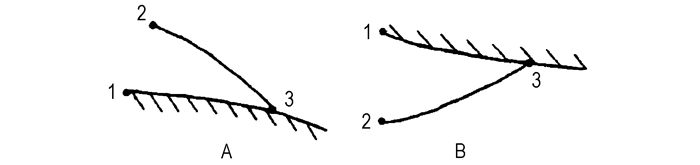
如图 2,对飞板的边界进行离散得到如下的差分格式:
| $ \left. \begin{align} &{{x}_{3}}-{{x}_{2}}={{k}_{2}}\left( {{y}_{3}}-{{y}_{2}} \right)\text{ } \\ &{{\theta }_{3}}-{{\theta }_{2}}=K[v\left( {{\rho }_{3}} \right)-v({{\rho }_{2}})] \\ \end{align} \right\} $ | (13) |
|
图 2 飞板边界差分示意图 Fig.2 Scheme of differences on flyer |
其中, k2=[cot(θ2+Kα2)+cot(θ3+Kα3)]/2,设k2=cotφ1,将上式和飞板的边界方程联立起来,利用特征线上的相容关系、流场压力表达式和离散的飞板运动边界方程,写出完整的飞板运动边界差分方程组:
| $ \left. \begin{align} &{{\theta }_{3}}={{\theta }_{1}}-K{{p}_{m}}[{{x}_{2}}-{{x}_{1}}-{{k}_{2}}\left( {{y}_{2}}-{{y}_{1}} \right)/\text{sin}({{\theta }_{1}}-{{\varphi }_{1}})\text{sin}{{\varphi }_{1}}~ \\ &{{\rho }_{3}}={{v}^{-1}}[{{\theta }_{3}}-{{\theta }_{1}}+v\left( {{\rho }_{2}} \right)] \\ &~{{i}_{3}}=e\left( {{\rho }_{3}} \right)+p\left( {{\rho }_{3}} \right){{\tau }_{3}}~ \\ &{{M}_{3}}=\sqrt{2\left( {{i}_{0}}-{{i}_{3}} \right)/c{{\left( {{\rho }_{3}} \right)}^{2}}}~ \\ &{{\alpha }_{3}}=\text{arcsin}\left( 1/{{M}_{3}} \right)\text{ } \\ &{{k}_{2}}=0.5[\text{cot}\left( {{\theta }_{2}}+{{\alpha }_{2}} \right)+\text{cot}\left( {{\theta }_{3}}+{{\alpha }_{3}} \right)]\text{ } \\ &{{\varphi }_{1}}=\text{arctan}\left( 1/{{k}_{2}} \right)\text{ } \\ &{{p}_{3}}={{p}_{1}}+0.5\left( {{\rho }_{1}}+{{\rho }_{3}} \right)\left( {{i}_{3}}-{{i}_{1}} \right)\text{ } \\ &{{p}_{\text{m}}}=0.5({{p}_{1}}+{{p}_{3}}) \\ \end{align} \right\} $ | (14) |
式(14)是利用迭代的方法求边界点3,而边界点还受pm、k2,φ1影响,因此,还需采用欧拉预估校正提高精度,计算3点的最终参数。取pm=p1,k2=cot(θ2+Kα2), φ1=θ2+Kα2的初值即可迭代成功,上述参数的下标表示插值的点,由式(14)迭代出θ3和pm。
再利用式(13)求得飞板在边界的位移:
| $ \left. \begin{align} &{{x}_{3}}={{x}_{1}}+K(\text{sin}{{\theta }_{3}}-\text{sin}{{\theta }_{1}})/{{p}_{\text{m}}}~ \\ &{{y}_{3}}={{y}_{1}}+K(\text{cos}{{\theta }_{3}}-\text{cos}{{\theta }_{1}})/{{p}_{\text{m}}} \\ \end{align} \right\} $ | (15) |
利用上述多方方程和JWL等熵方程的特征线差分法编写计算程序对飞板的抛掷姿态进行计算。下面分别计算TNT炸药和乳化炸药作用下飞板的运动规律,取不同质量比R, 分别计算其在不同质量比的飞板的飞行参数,并对它们的抛掷曲线进行对比研究。飞板材料采用铝板,密度ρ为2.71 g·mm-3, 部分特定炸药的JWL系数[8]见表 1。
| 表 1 JWL状态方程参 Tab.1 Parameters of JWL equation of state |
由于篇幅的原因,分别取质量比R=1.0、R=1.5,采用JWL等熵方程和多方方程的特征线法分别计算TNT和乳化炸药作用下的飞板的焊接参数,绘制飞板的抛掷曲线,并比较不同炸药在一系列质量比下飞板参数的相互关系。
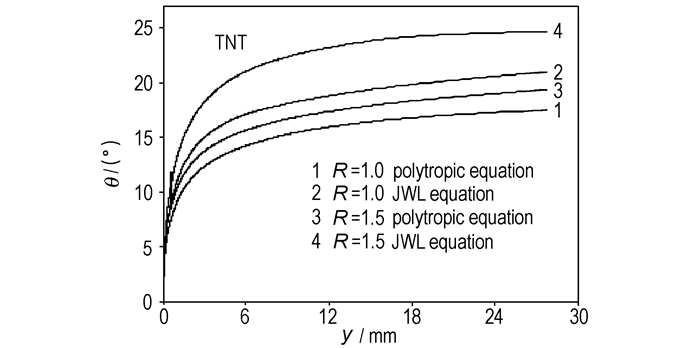
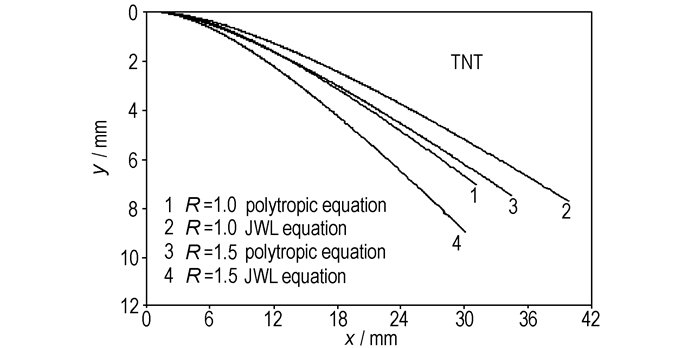
图 3和图 4是TNT炸药在不同质量比R=1.0、R=1.5条件下采用两种等熵方程计算得到的飞板的抛掷曲线。通过图 3和图 4,我们可以看出飞板的抛掷角总体变化趋势是随着竖向位移的增大而增大,当位移达到一定的程度时,抛掷角将保持稳定的状态。在相同的质量比和相同的位移条件下,采用JWL等熵方程计算得到的抛掷角大于采用多方方程得到的抛掷角;在相同的水平位移下,应用JWL等熵方程计算得到的竖向位移小于采用多方方程得到的竖向位移。
|
图 3 飞板的竖向位移和抛掷角的相互关系 Fig.3 Relationship between vertical displacement and bending angle |
|
图 4 飞板的水平位移和竖向位移的关系 Fig.4 Relationship between horizontal displacement and vertical displacement |
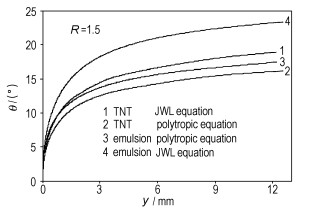
图 5和图 6表示的是TNT和乳化炸药在质量比为R=1.5时,飞板的抛掷曲线的对比关系。由图 5得知:在相同的竖向位移下,TNT炸药得到的飞板的最大抛掷角小于乳化炸药得到的;而采用JWL等熵方程计算得到的飞板的抛掷角大于采用多方方程计算得到的抛掷角, 这是由于多方状态方程描述爆轰产物的压力衰减较快,而JWL等熵方程则能更好的表示爆轰产物压力的分布。
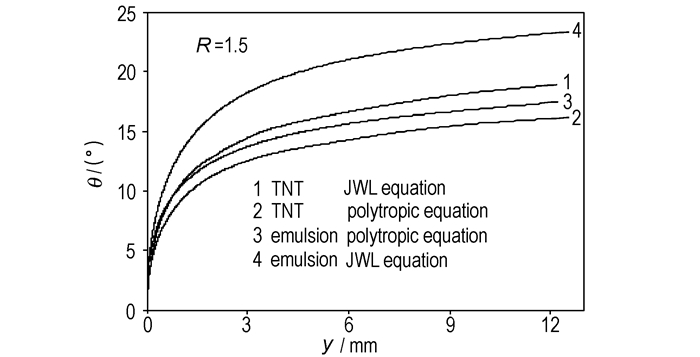
|
图 5 飞板的竖向位移和抛掷角的相互关系 Fig.5 Relationship between vertical displacement and bending angle |
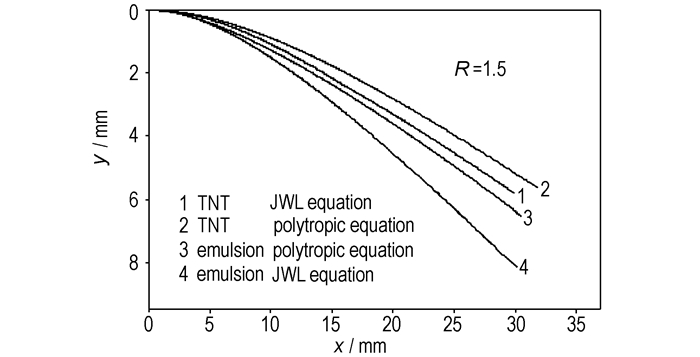
|
图 6 飞板的水平位移和竖向位移的关系 Fig.6 Relationship between horizontal displacement and vertical displacement |
从图 6可以看出,在相同的水平位移下,JWL等熵方程计算得到的竖向位移大于采用多方方程得到的竖向位移;而且在相同的条件下,TNT炸药计算得到的位移小于乳化炸药得到的。
4.2 Richter公式验证为了描述通用状态方程的特征线法研究的准确性,采用二维Richter计公式对相同的炸药进行计算,并对两种不同的计算方法的计算结果进行对比研究。(Richter公式是在爆轰产物作用在飞板上,飞板的压力分布与飞板的抛掷角成正比的假设条件下导出的二维近似计算方法。尽管该方法在数学处理上较为粗糙,但由于其计算简单,有较好的计算精度,被广泛应用于爆炸焊接的计算中。)下面是采用Richter方法计算TNT爆轰驱动飞板的飞行参数,并与通用状态方程计算得到的飞板飞行参数进行比较,来验证通用状态方程的准确性。图 7和图 8分别为采用了两种方法计算得到的飞板的飞行姿态的对比关系,由图可知,通用状态方程的特征线法计算得到的抛掷角小于Richter计算得到的结果,这样的关系符合Richter模型计算结果往往偏大的特点。
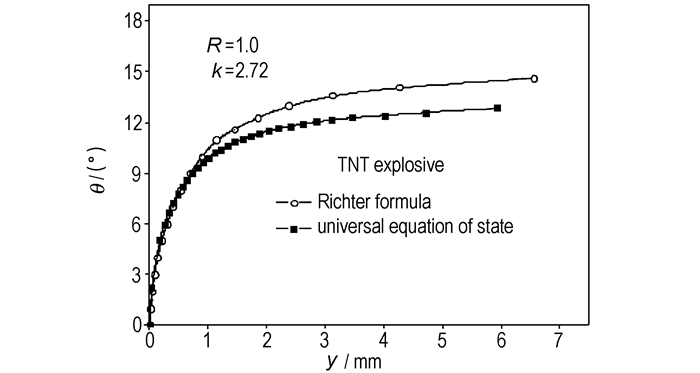
|
图 7 飞板竖向位移和抛掷角的对比关系 Fig.7 Comparative relationship between vertical displacement and bending angle of flyer plate |
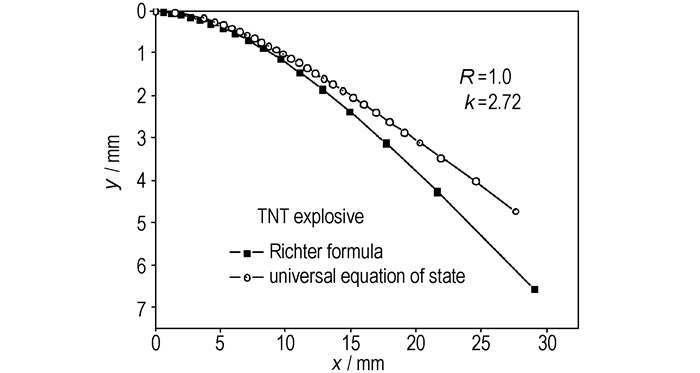
|
图 8 飞板水平位移和竖向位移的对比关系 Fig.8 Comparative relationship between horizontal displacement and vertical displacement of flyer plate |
(1) 采用了多方气体的特征线法推导了JWL等熵方程下的二维特征线法,由于特征线方程与气流的物态方程无关,所以是一种通用状态方程的特征线关系。
(2) 利用两种特征线法计算了滑移爆轰中TNT和乳化炸药对飞板的驱动作用,得到了不同质量比R下飞板的抛掷曲线。
(3) 通过对比研究不同炸药在不同质量比时飞板的抛掷曲线,可以得到如下的结论:质量比越大,飞板的抛掷角也越大;在相同的竖向位移下,采用JWL等熵方程计算得到的抛掷角大于利用多方方程特征线法计算得到的抛掷角;因为JWL等熵方程描述炸药的爆轰压力的衰减要比多方方程的爆轰压力衰减得慢,故JWL等熵压力对飞板的驱动作用时间相对较长。因此,要想达到相同的竖向位移,JWL等熵方程需要的飞板的抛掷角较大,才能实现基板和飞板的顺利焊接。
(4) 由Richter公式验证可知,利用Richter计算公式得到的飞板的飞行参数相对于JWL等熵方程的特征线法得到飞行参数要大一些,这是由于Richter二维计算模型考虑了滑移爆轰和起爆端的稀疏作用,与实际情况近似,但它忽略了飞板运动过程中空气阻力的影响,所以造成Richter公式计算得到的飞板参数结果往往偏大,这是造成两种方法不同的原因。而JWL等熵方程能更好地描述炸药的爆轰压力,故对比研究表明,通用状态方程的特征线法计算结果优于Richter方法。
| [1] |
郭佑雄, 赵福兴, 周祖荣. 滑移爆轰作用下飞板运动规律的研究-双P-M法[J].
爆炸与冲击, 1998, 18(2): 123-130. GUO You-xiong, ZHAO Fu-xing, ZHOU Zu-rong. An approximate method on describing the movement of plate under sliding detonation-twin P-M method[J]. Explosion and Shock Waves, 1998, 18(2): 123-130. |
| [2] |
邵丙璜, 张凯.
爆炸焊接原理及其工程应用[M]. 大连: 大连工学院出版社, 1987.
SHAO Bing-huang, ZHANG Kai. Explosion Welding Theory and Application[M]. Dalian: Dalian University of Technology Press, 1987 |
| [3] |
王飞, 王连来, 刘广初. 飞板运动规律的特征线法研究[J].
解放军理工大学学报, 2005, 6(4): 374-377. WANG Fei, WANG Lian-lai, LIU Guang-chu. Flier plate research with difference method in characteristic line[J]. Journal of PLA University of Science and Technology, 2005, 6(4): 374-377. |
| [4] |
陶刚. 拉伐尔喷管射流中喷口激波处理的特征线法[J].
弹道学报, 2002, 12(4): 45-49. TAO Gang. Characteristics method on processing shock wave in supersonic jet for Laval nozzle[J]. Journal of Ballistics, 2002, 12(2): 45-49. |
| [5] |
张兆顺, 崔桂香.
流体力学[M]. 北京: 清华大学出版社, 1999.
ZHANG Zhao-shun, CUI Gui-xiang. Hydrodynamics[M]. Beijing: Tsinghua University Press, 1999 |
| [6] |
张凯, 李晓杰. 滑移爆轰下带覆盖平板抛掷的理论与计算[J].
大连理工大学学报, 1988, 28(1): 29-31. ZHANG Kai, LI Xiao-jie. Theory and calculation of flyer plate motion under action of glancing detonation of explosive with a cover[J]. Journal of Dalian University of Technology, 1988, 28(1): 29-31. |
| [7] |
徐锡申, 张万箱.
实用物态方程理论导引[M]. 北京: 科学出版社, 1986: 405-406.
XU Xi-shen, ZHANG Wan-xiang. Practical Guidance Equation of State Theory[M]. Beijing: Science Press, 1986: 405-406. |
| [8] |
张宝  , 张庆明, 黄风雷.
爆轰物理学[M]. 北京: 兵器工业出版社, 2006: 160-163.
, 张庆明, 黄风雷.
爆轰物理学[M]. 北京: 兵器工业出版社, 2006: 160-163.
ZHANG Bao-ping, ZHANG Qin-ming, HUANG Feng-lei. Detonation Physics[M]. Beijing: Oranance Industry Press, 2006: 160-163. |
The movement of flyer plate was investigated with characteristic curve method in sliding detonation.



