2. 中国工程物理研究院化工材料研究所, 四川 绵阳 621900
2. Institute of Chemical Materials, CAEP, Mianyang 621900, China
炸药元件在实际使用中,有可能发生跌落情况。炸药从不同高度跌落后的响应情况,是炸药安全性和可靠性分析的重要依据。通常跌落试验方法,研究炸药跌落响应。例如Spigot跌落试验,主要是模拟大型药柱跌落的试验,用于研究炸药在低冲击的响应过程,评定大型炸药同时受到机械撞击、剪切力、摩擦力及绝热压缩时的安全性能[1]。Chidester等人[2]针对HMX基炸药进行了低冲击试验,获得了炸药在不同撞击速度下响应结果,并采用点火增长模型对其低冲击反应过程进行数值计算。韩勇等人[3]分析了炸药代用材料在低冲击下的力学响应。代晓淦等人[4]建立了模拟跌落试验方法。由于炸药跌落试验中难以精确测量,试验成本又相对较高,因此,对炸药跌落过程的计算分析更显重要。通过计算分析,能有效获得炸药跌落响应细节的变化规律。
本研究针对Spigot跌落试验,建立了二维的数值计算模型,采用不同响应模型描述炸药起爆、点火和破碎。对高感度的JO-9159炸药和低感度的PBXC03炸药的跌落过程进行了数值模拟分析。
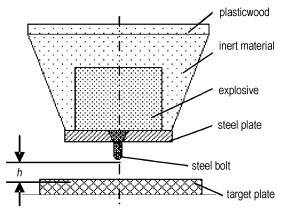
2 spigot跌落试验图 1为Spigot试验装置图,被测炸药放置于惰性材料中,炸药下端是安有钢栓的钢板。炸药、惰性材料、钢板和钢栓组成跌落体。跌落体下一定距离处放置钢质靶板,靶板放置在水泥地面上。试验时,将跌落体提升至预定高度h,跌落体从空中自由下落后撞击到靶板上,钢栓受到靶板的作用后,对炸药产生强烈的机械撞击、剪切、摩擦等作用,使炸药样品发生反应。根据对试验残余物的收集观察、高速摄影与空气冲击波超压来评定炸药及炸药部件响应情况,从而分析炸药在不同高度跌落的安全性。炸药试样为圆柱体,直径为152 mm,高为102 mm。钢栓和靶板为钢材料,钢栓高38 mm,上表面直径30 mm。
|
图 1 试验装置简图 Fig.1 Sketch map of experimental device |
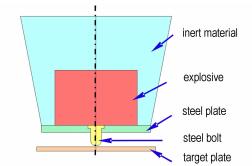
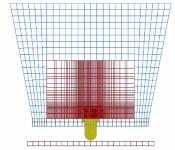
采用非线性有限元计算方法[5],对Spigot跌落试验进行了数值模拟计算。图 2是根据试验装置建立的计算模型。模型中各个部件的尺寸与试验模型相同。由于模型呈轴对称性,建立了二维轴对称模型。为了减少计算量,建立模型时,炸药及其部件建立在距靶板较低的高度,给定初速度值并设置重力加速度,描述跌落体的自由下落过程。靶板底面施加零位移约束来模拟地面。为了观察炸药试样的变形和反应情况,整个模型采用拉格朗日算法。钢栓、靶板和代用材料采用塑性动力学材料模型。图 3为计算网格图,在保证计算精度的前提下减小计算量,对炸药中与钢栓作用的附近区域使用细网格,以方便观察炸药变形。
|
图 2 计算模型 Fig.2 Calculating model |
|
图 3 计算网格图 Fig.3 Calculating mesh |
采用点火增长模型[6]和JWL状态方程[7]描述实验炸药起爆轰过程。点火增长模型:
| $ \begin{array}{l} \frac{{{\rm{d}}\lambda }}{{{\rm{d}}t}} = I{\left( {1-\lambda } \right)^b}{\left( {\frac{\rho }{{{\rho _0}}}-1-a} \right)^x} + \\ \;\;\;\;\;\;\;{G_1}{\left( {1 - \lambda } \right)^e}{\lambda ^d}{p^y} + {G_2}{\left( {1 - \lambda } \right)^e}{\lambda ^g}{p^z} \end{array} $ | (1) |
式中, λ为炸药反应度;t为时间;ρ为密度;ρ0为初始密度;p为压力;I,G1,G2,a,b,x,c,d,y,e,g和z为拟合的系数。表 1给出了JO-9159炸药点火增长模型的模型参数[8]。
| 表 1 JO-9159炸药点火增长反应模型参数[8] Tab.1 Reaction parameters in I&G model of JO-9159 |
采用热力耦合方法计算炸药点火和破碎情况。炸药用塑性动力学材料模型描述,其应力应变关系为[9]
| $ \left\{ \begin{array}{l} \sigma = E\varepsilon \;\;\;\sigma < {\sigma _s}\\ \sigma = {E_t}\varepsilon \;\;\sigma \ge {\sigma _s} \end{array} \right. $ | (2) |
在加载段应力σ与应变ε保持线性,当应力大于屈服应力σs时,材料进入塑性,此后如果继续加载,应力应变关系仍然为线性,但是斜率发生变化,卸载曲线与加载段曲线斜率相同,当完全卸载后,材料中将保留塑性变形εp。
在二维条件下,判断材料是否进入塑性,使用V.MISE屈服准则,即
| $ \frac{1}{2}{s_{ij}}{s_{ij}}-\frac{1}{3}\sigma _{_s}^{^2} = 0 $ | (3) |
(3) 式中,sij=σij-1/3(σ11+σ22)δij,为斜应力张量,当等效应力等于屈服应力时,材料开始进入塑性变形。
采用各向同性热材料模型描述炸药受力的热作用,实现热和力的耦合计算。根据能量守恒原理,热问题的基本有限元方程可由热平衡方程推导求得[10]
| $ \left[C \right]\left\{ {{T^\& }} \right\} + \left[{{K_T}} \right]\left\{ T \right\} = \{ Q\} $ | (4) |
式中, [C]为比热矩阵,考虑系统内能的增加;[KT]为热传导矩阵,包括导热系数、对流系数及辐射率和形状系数;{T}为节点温度向量;{T&}为温度对时间的导数;{Q}为节点热流率向量。
| $ \left[{\begin{array}{*{20}{c}} {\left[0 \right]}&{\left[0 \right]}\\ {\left[0 \right]}&{\left[C \right]} \end{array}} \right]\left\{ \begin{array}{l} [{u^\& }]\\ [{T^\& }] \end{array} \right\} + \left[{\begin{array}{*{20}{c}} {\left[K \right]}&{[0]}\\ {[0]}&{[{K_T}]} \end{array}} \right]\left\{ \begin{array}{l} \left[u \right]\\ \left[T \right] \end{array} \right\} = \left\{ \begin{array}{l} \left[F \right]\\ [Q[ \end{array} \right\} $ | (5) |
式中, {u}为节点位移向量;{u&}为节点速度向量;{F}为力向量,包括施加的节点力和由热应变引起的力; [K]为刚度矩阵。
考虑炸药温度增加后的自热反应,采用Arrhenius方程进行描述:
| $ S = \rho QZ\exp (-\frac{E}{{RT}}) $ | (6) |
式中, S为源项;ρ为炸药密度;Q为反应热;Z为指前因子;E为活化能;R为普适气体常数;T为温度。
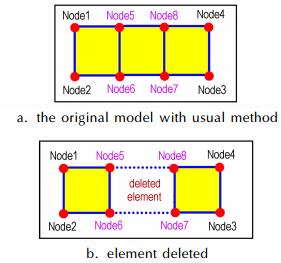
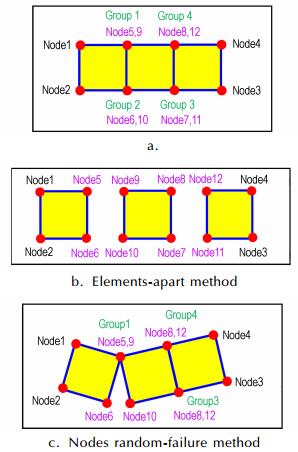
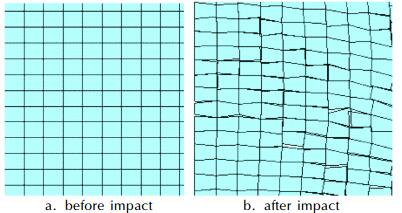
计算炸药破碎时,需要描述炸药的变形及裂纹的扩展,如果将炸药设为连续网格单元,单元受到作用产生较大变形时,计算时为了避免计算的不收敛,会将网格单元删除,如图 4所示,这样不能够描述炸药单元的热量积累,也与实际炸药破碎过程有很大差别。本研究采用了网格分离和节点随机失效的方法,对炸药计算单元进行描述。将炸药设为由众多独立的网格单元组合的结构,对不同单元中相同位置的节点建立节点组,并设置节点分离的失效值,当应变达到失效值之后会使节点分离。使组合网格单元分开,从而能够描述炸药裂纹形成和破碎,如图 5(b)所示。因为炸药材料并非完全均匀,其力学性能有差异,在同样力的作用下,炸药裂纹产生和破碎会呈现随机性。为了模拟炸药随机破裂过程,将节点组的分离值设置为符合正态分布的随机变量,描述炸药在跌落过程中随机破裂过程,如图 5(c)所示。图 6(a)是受力前炸药网格结构图。图 6(b)是受力后炸药网格结构图,可以看到炸药裂纹的随机形成。
|
图 4 连续单元模型的网格删除原理 Fig.4 Elements deleted progress in continuous model |
|
图 5 网格节点分离随机失效模型的节点分离原理 Fig.5 Fragments with elements-apart method and nodes random-failure |
|
图 6 受力前后炸药裂纹形成 Fig.6 Cracks and fragments in explosive before and after press |
对炸药跌落过程进行计算时,先采用点火增长模型计算炸药起爆过程,获得炸药起爆的跌落阈值速度,再用热力耦合模型计算炸药点火阈值速度并分析炸药破碎情况。
这里选择感度不同的PBXC03(HMX/TATB/粘合剂/87/7/6)和JO-9159(HMX/粘合剂/95/5)两种炸药进行计算,综合分析炸药在跌落过程中的不同响应状态。对于PBXC03炸药,采用点火增长模型计算发现:即使炸药在高速触地(跌落速度为100 m·s-1)时,PBXC03炸药也不会发生爆轰响应。而对于JO-9159炸药,即使触地时的速度很低(跌落速度为5 m·s-1)也会发生爆轰。以这两种炸药为研究对象,就可以模拟出炸药跌落过程中可能出现的所有响应程度:
(1) PBXC03炸药在Spigot跌落试验过程中,只可能发生点火和碎裂两种反应,采用塑性动力学和热力耦合方法计算炸药跌落过程中的碎裂和点火过程。
(2) JO-9159炸药则采用点火增长模型,描述跌落过程炸药的爆轰响应过程。
本研究以这两种炸药为研究对象,采用不同计算方法计算其跌落过程,分析跌落过程中炸药不同程度的响应程度。
表 2为计算得到的不同跌落速度及其对应跌落高度下PBXC03炸药响应情况。从表中可以看出,炸药发生反应的临界跌落速度在25~28 m·s-1之间,对应的跌落高度在30~40 m之间。而实验测量跌落临界阈值速度在25.5~27.7 m·s-1之间(该试验数据由中国工程物理研究院化工材料研究所提供),计算值与实验值相吻合。而JO-9159炸药敏感度较高,即使在低速撞击时,即当跌落速度低于5m·s-1时,也会发生爆轰反应。因此只对JO-9159炸药进行爆轰分析。
| 表 2 计算的不同跌落速度下PBXC03炸药响应情况 Tab.2 Calculated reaction results at different velocities for PBXC03 |
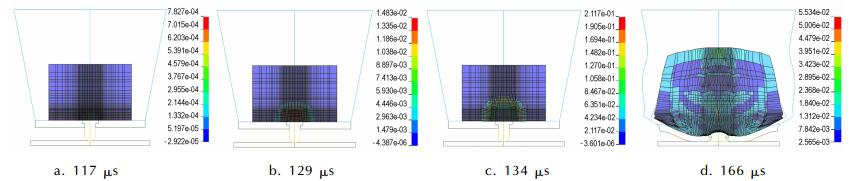
以JO-9159炸药为例,分析炸药的起爆过程。图 7是跌落速度为20 m·s-1时,JO-9159炸药起爆时的不同时刻内部压力分布。117 μs时,钢栓底部开始接触靶板后,其上表面作用于炸药试样,在钢栓的作用下,炸药底部产生压力,压力较低;随着钢栓不断的作用,炸药内部压力成环形逐渐向炸药内部成长,129 μs时,炸药内部最高压力达到1.48 GPa,134 μs时,炸药内部最高压力达21 GPa,可正常爆轰;166 μs时,炸药完全爆轰。
|
图 7 不同时刻JO-9159炸药试样内部纵界面压力分布 Fig.7 Pressure distributions at different time for JO-9159 |
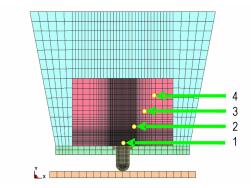
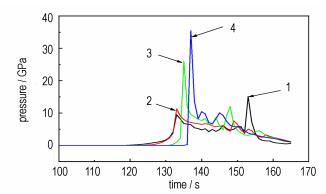
为进一步观察炸药内部反应情况,在炸药试样的纵界面选取5个网格,图 8是所取网格的位置,图 9给出了他们的压力时间曲线。从图 9中可以看出,1、2、3、4号4个单元的压力依次升高,说明炸药内部压力的成长方向是由底面向炸药内部成长的,137 μs时,4号网格的压力已经达到了32 GPa,说明此时炸药已经发生完全爆轰。
|
图 8 JO-9159炸药试样内部纵界面所取网格位置 Fig.8 Elements' position in explosive of JO-9159 |
|
图 9 JO-9159炸药试样内部取节点的压力时间曲线 Fig.9 Pressure vs time of monitor elements for JO-9159 |
图 10给出了不同跌落速度下,PBXC03炸药最高温度点的温度时间曲线。在跌落速度低于25 m·s-1时,PBXC03炸药受力后温度升高,当达到一定温度后便不再升高,说明此速度下炸药不会发生点火。当跌落速度大于28 m·s-1时,炸药受力后温度上升,达到一定温度后继续减慢上升,出现温度平台,但随后温度出现突跃上升,表明炸药发生点火,并且点火时间出现了一定的延迟。从图中可以看出,随着跌落速度的增大,温度平台变小,点火延迟时间缩短。
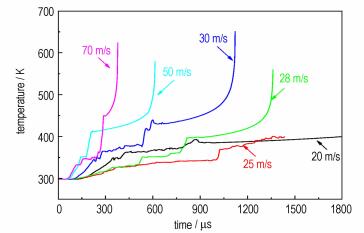
|
图 10 不同跌落速度下高温点的温度时间曲线 Fig.10 Temperature vs time of the highest point at different drop velocities for PBXC03 |
图 11是跌落速度为20 m·s-1时,不同时刻PBXC03炸药变形图。111 μs时钢栓接触到靶板,开始作用于炸药试样,炸药在钢栓的作用下开始发生变形,但还没有发生节点失效,没有形成裂纹。300 μs时,在钢栓的压缩、剪切和摩擦的共同作用下,与钢栓顶角接触处的炸药节点首先分离,网格变形,产生裂纹。此后,炸药在钢栓的作用下,裂纹主要发生在与钢栓上部及与钢栓顶角接触点附近,裂纹斜向上伸展。1200 μs时,与钢栓顶角接触的炸药部分发生破碎。2000 μs时,钢栓大部分已进入炸药内部,炸药内部裂纹进一步扩大。
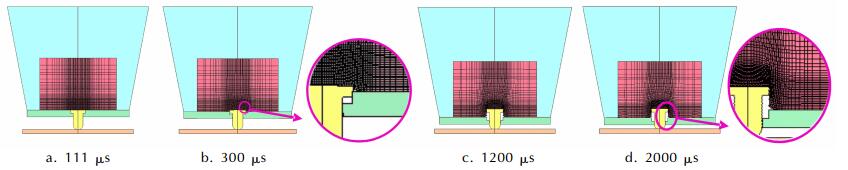
|
图 11 跌落速度为20 m·s-1时,不同时刻PBXC03炸药变形 Fig.11 Explosive deformation at drop velocity of 20 m·s-1 for PBXC03 |
图 12是跌落速度为20 m·s-1时,不同时刻PBXC03炸药内部温度分布。111 μs时,与钢栓接触处的炸药受到钢栓的作用,温度升高;300 μs时,钢栓周围炸药的温度继续升高,与钢栓发生剪切作用处的温度升至最高;876 μs时,炸药内部温度最高温度达到394 K,之后炸药最高温度维持在400 K左右波动,并未发生点火。
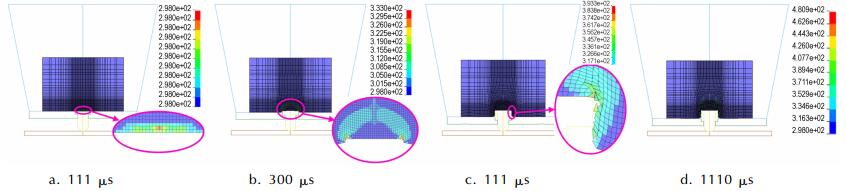
|
图 12 跌落速度为20 m·s-1时,不同时刻PBXC03炸药内部温度分布 Fig.12 Temperature distributions at drop velocity of 20 m·s-1 for PBXC03 |
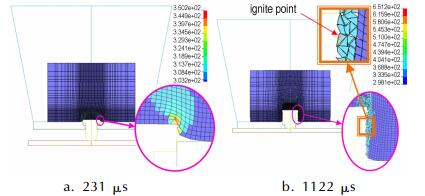
图 13是触地速度为30 m·s-1时,不同时刻PBXC03炸药内部温度分布。231 μs时,由于钢栓的剪切作用,与钢栓接触炸药网格受到挤压,温度升高。1122 μs时,随着钢栓的持续作用,钢栓顶部边界的炸药网格脱落形成颗粒,这些颗粒温度升高,热量不断积累,最终发生点火。
|
图 13 跌落速度为30 m·s-1时,不同时刻PBXC03炸药内部温度分布 Fig.13 Pressure distribution of PBXC03 at drop velocity of 30 m·s-1 |
采用炸药点火增长模型能够有效计算跌落试验中炸药起爆临界速度。而利用热力耦合炸药自热反应模型可以判断炸药是否被点燃。采用网格分离和节点随机失效的计算方法,能够描述炸药变形和破碎。利用数值计算方法对炸药跌落过程进行安全性评价分析时,先计算炸药起爆阈值,再计算炸药点火阈值,然后对炸药碎裂变形进行计算,可实现对炸药跌落中不同响应情况的分析。本文计算的PBXC03炸药发生反应的临界跌落速度在25~28 m·s-1之间,而实验测量跌落临界阈值速度在25.5~27.7 m·s-1之间,计算值与实验值相吻合。但计算中如何选取炸药强度失效和热反应模型参数,是正确计算炸药点火反应的关键,需要进一步开展研究。
| [1] |
孙业斌, 慧君明, 曹欣茂, 等.
军用混合炸药[M]. 北京: 兵器工业出版社, 1995: 53-54.
|
| [2] |
Chidester S K, Green L G, Lee C G. A Frictional Work Predictive Method for the Initiation of Solid High Explosives from Low Pressure Impacts[C]//10th International Detonation Symposium, Office of Naval Research, Boston MA, 1993: 785-792.
|
| [3] |
韩勇, 向永, 韩敦信, 等. Steven试验中模拟材料D-90031力学响应的数值模拟[J].
含能材料, 2004, 12(z2): 545-547. HAN Yong, XIANG Yong, HAN Dun-xin, et al. The numerical modeling of dynamical response of D-90031 in STEVEN test[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao)(sup), 2004, 12(Z2): 545-547. DOI:10.3969/j.issn.1006-9941.2004.z2.051 |
| [4] |
代晓淦, 申春迎, 文玉史. 模拟跌落撞击下PBX-2炸药的响应[J].
含能材料, 2011, 19(2): 209-211. DAI Xiao-gan, SHEN Chun-ying, WEN Yu-shi. Reaction of PBX-2 explosive under simulated drop impact[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2011, 19(2): 209-211. |
| [5] |
Lawrence livermore national laboratory. LS-DYNA Μser's Manual[M]. California, University of California, Lawrence Livermore National Laboratory, 2001.
|
| [6] |
Tarver C M, Hallquist J O, Erickson L M. Modeling of short pulse duration shock initiation of solid explosive[C]//Proceedings of 8th Symposium (International) on Detonation, Albuquerque: [s. n. ]. 1985: 951-961.
|
| [7] |
Lee E, Breithaupt D, Mcmillan C, et al. The motion of thin metal walls and the equation of state of detonation products, UCRL-91490[R]. Albuquerque: [s. n. ]. 1985.
|
| [8] |
柯加山. 冲击条件下炸药的起爆现象研究[D]. 北京: 北京理工大学, 2002.
|
| [9] |
白金泽.
LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005: 47-49.
BAI J Z. LS-DYNA 3D theory foundation and case analysis[M]. Beijing: Science press, 2005: 47-49. |
| [10] |
陶文栓, 李永堂.
热工程学[M]. 武汉: 武汉理工大学出版社, 2001.
TAO W S, LI Y T. Thermal engineering[M]. Wuhan: Wuhan University of Technology Press, 2001 |
| [11] |
HU Zhong, ZHU Li-Hua, WANG Bei-yi, et al. Computer simulation of the deep extrusion of a thin-walled cup using the thermo-mechanically coupled elasto-platic FEM[J].
Journal of Materials Processing Technology, 2000, 102(1): 128-137. |
The numerical model of spigot test was developed. The elements-apart method was used to describe fragmentation of explosive. The critical drop velocity, inside temperature and fragmentation of explosive were calculated.



 ,
,