未来战场要求武器系统能适应信息化、精确化、多功能化趋势, 要求弹药能对付战场中出现的多种目标^[1]，如坦克、步兵战车、通信指挥车、装甲运输车以及超低空飞行器等。为使同一弹药能对付战场中出现的多种目标，网栅切割式MEFP成为多功能战斗部技术研究的热点问题之一。对于防护能力较强的装甲目标，网栅切割式MEFP战斗部形成单个EFP攻击目标；对于防护能力较弱、需要通过面毁伤才能有效摧毁的目标，如武装直升机、装甲车等，则形成多个子EFP，实现一弹多用的目的，从而有效地提高战斗部作战使用效能。郭美芳等^[1]初步分析了药形罩的材料与结构、炸药的类型与装药结构对多模式战斗部性能的影响，说明了多模式战斗部技术的重要性。张洋溢等^[2]分析了一种在药型罩前适当位置安装一个可抛掷的十字形切割网栅的装药结构，结果表明，该装药结构产生的破片能够穿透48 m处的6 mm的45^#钢板，可以用来打击直升机等轻型装甲目标。李伟斌等^[3]分析了主装药端面中心点起爆和药型罩顶点起爆爆轰波传播规律，实现了杆式EFP、EFP两种模态的转换。这些研究集中于对十字形网栅切割式MEFP的数值模拟分析和起爆点位置对EFP模态转换的影响，未能研究起爆点位置对圆环形网栅切割式MEFP成型的影响。本文对在药型罩前适当位置安装一个圆环形切割网栅的战斗部结构做了数值模拟，分析了起爆点与药型罩顶点的轴向距离对MEFP成型的影响，实现了一弹多用的目的, 对进一步研究多模式战斗部具有一定的参考价值。

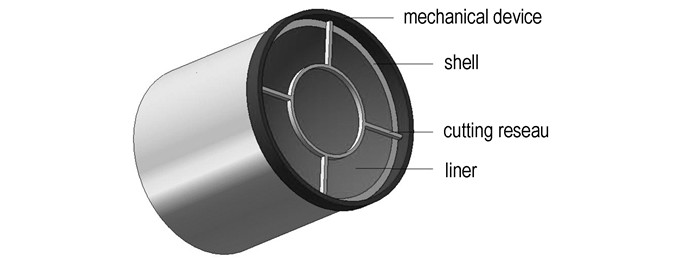
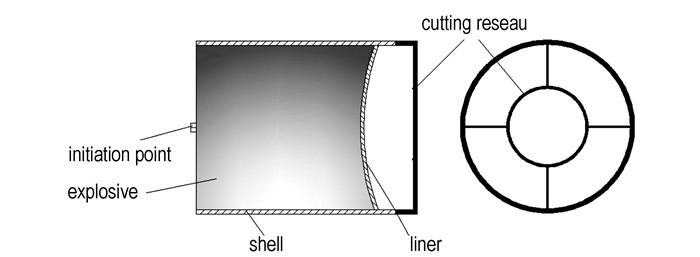
网栅切割式MEFP战斗部结构设计见图 1，主要由铜药型罩、切割网栅、壳体和炸药组成。图 2为网栅切割式MEFP战斗部结构剖视图。

图 1(Fig. 1)

图 1 圆环形网栅切割式MEFP战斗部 Fig.1 Circle-shaped MEFP warhead

图 2(Fig. 2)

图 2 圆环形网栅切割式MEFP战斗部结构剖视图 Fig.2 Sectional view of the Circle-shaped MEFP warhead

考虑到若在数值模拟计算中采用传统的拉格朗日网格模拟炸药的爆轰过程，炸药网格会出现严重的畸变现象，不利于计算的进行。为避免上述问题的出现，采用流固耦合方法对药型罩的切割过程进行了模拟。其中炸药和空气网格均采用单点欧拉多材料体单元，炸药周围用空气网格填充；药型罩、壳体和切割网栅采用拉格朗日六面体网格单元，并且耦合在空气网格中。

药型罩采用等壁厚设计，材料为紫铜，口径为90 mm，壁厚为4.0 mm，曲率半径R=140 mm，采用MAT_JOHNSON_COOK模型GRUNEISEN状态方程来描述其动态响应过程，基本参数见表 1；装药为8701炸药，装药高度h=90 mm，其本构模型选用MAT_HIGH_EXPLOSIVE_BURN高能炸药材料模型和JWL状态方程，基本参数见表 2；选用钢质壳体。网栅中心圆环的直径d_c=40 mm，材料为钨，相关参数见表 3；空气材料采用流体模型为：MAT_NULL，状态方程为线性多项式：EOS_LINER_POLY_NOMIAL来描述，基本参数见表 4。起爆方式选择单点起爆，起爆点在装药底面圆心处。

表 1(Tab. 1)

表 1 装药材料参数[4] Tab. 1 Material parameters of the charge materials D/km·s-1 ρ0/g·cm-3 pcj/GPa A/GPa B/GPa R1 R2 e0 ω RHT-901 7.89 1.717 29.5 524.23 7.678 4.2 1.1 8.5 0.34 Note: D，detonation velocity；ρ0，mass density of RHT-901；pcj，Hapman-Jouget pressure；A，B，R1，R2，ω，coefficient；e0，specific internal energy.

表 1 装药材料参数[4] Tab.1 Material parameters of the charge

表 2(Tab. 2)

表 2 药型罩的状态方程计算参数[5] Tab. 2 Computational parameters of liner state equation materials ρ1/g·cm-3 C/m·s-1 S1 S2 S3 C0 a E0/ GPa red copper 8.96 4750 3.8 2.74 0.125 1.346 0.34 0.0 Note: ρ1，mass density of red copper；C，sound velocity in the red copper；S1，S2，S3，C0，grunaisen parameter；a，volume correction factor；E0，initial energy of unit volume.

表 2 药型罩的状态方程计算参数[5] Tab.2 Computational parameters of liner state equation

表 3(Tab. 3)

表 3 钨丝的材料模型主要参数[2] Tab. 3 Material parameters of the tungsten materials ρ2/g·cm-3 G/GPa A B n C m Tm/K Tr/K cv/J·kg-1·K-1 tungsten 19.3 160 0.0135 0.00177 0.61 0.023 1.0 1723 298 142 Note: ρ2，mass density of tungsten；A，yeld stress constant；B，strain-hardening constant；n，strain-hardening index；C，strain-rating correlation coefficient；m，temperature correlation coefficient；Tm，melting temperature；Tr，room temperature；cv，specific heat capacity.

表 3 钨丝的材料模型主要参数[2] Tab.3 Material parameters of the tungsten

表 4(Tab. 4)

表 4 空气模型计算参数[3] Tab. 4 Computational parameters of air model ρ3/g·cm-3 C/m·s-1 E0/kJ·cm-3 V0 1.25E-3 394 0 1 Note: ρ3，mass density；C，sound velocity；E0，initial internal energy；V0，initial relative volume.

表 4 空气模型计算参数[3] Tab.4 Computational parameters of air model

炸药起爆后，在爆轰波作用下，药型罩发生极大的塑性变形而被压垮、翻转。翻转后的罩体除获得很高的质心速度外，罩微元还获得沿轴向近似呈线性分布的轴向及径向速度^[5]。处于流体状态的药型罩碰撞金属网栅，被切割成5个子EFP，子EFP在爆轰产物的作用下继续被加速、翻转，不同的子EFP具有不同的径向速度和轴向速度, 使药型罩形成具有一定速度梯度的5个部分, 进而形成具有一定形状的高速侵彻体。由于药型罩中心部分先于周边部分受到爆轰波的作用，所以中心子EFP的速度高于周边子EFP，结果是速度最快的中心子EFP走在最前面, 单独成为一个部分，而后面的则形成4个轴向速度，相差不大，但径向存在一定速度的子EFP。药型罩最终形成5个子EFP的新的毁伤元，速度在1600~2400 m·s^-1范围内。

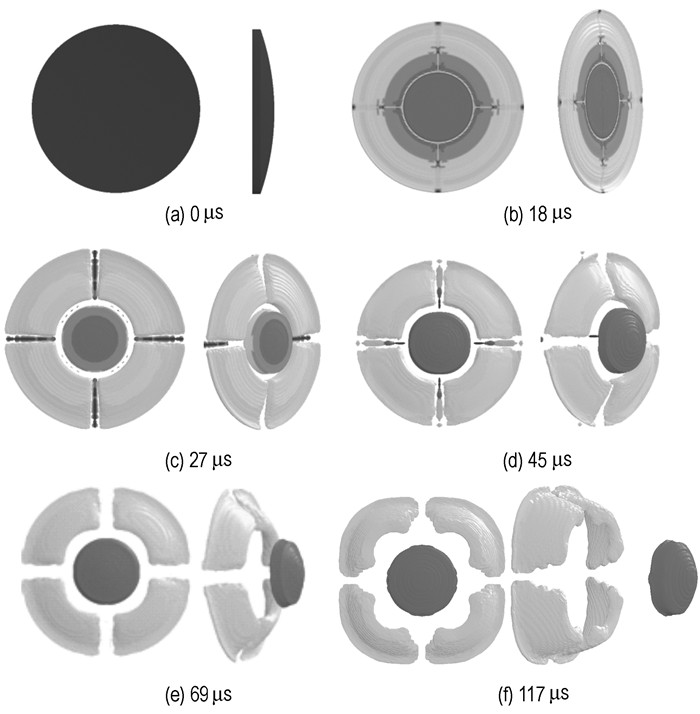
图 3(a-f)所示爆炸成型弹丸各个时刻成型结果及速度云图。圆环形网栅切割式MEFP的成型过程表明, 0~17 μs在爆轰波的作用下，药型罩微元存在轴向速度，各个部位在运动中存在挤压现象，药型罩中部会逐渐增厚，同时药型罩逐渐翻转。18 μs时刻翻转的药型罩碰撞金属网栅，实施切割。27 μs时刻药型罩被金属网栅切割成5个独立的部分，并继续向前飞行。45 μs时刻由于子EFP头尾仍存在速度差，在运动过程中将产生拉长。46~116 μs期间，子EFP处于轴向拉伸的状态，并且以递增的速度向前飞行。在117 μs时刻形成具有良好的气动外形和一定长径比的子EFP，并且速度达到稳定。

图 3(Fig. 3)

图 3 网栅切割式MEFP成型过程及速度云图(主视图及左视图) Fig.3 The forming processes and velocity distributions of MEFP (front view and left view)

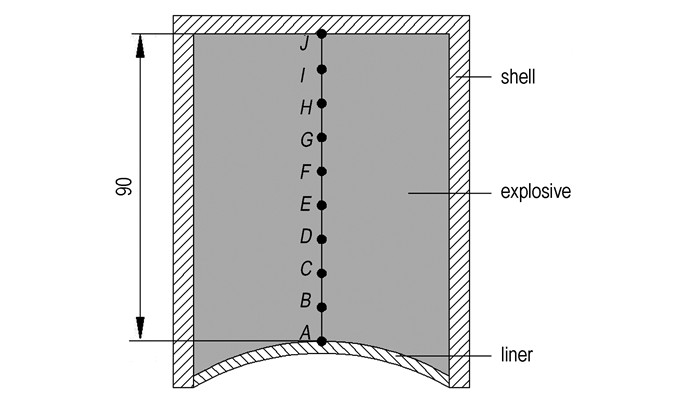
成型装药结构采用圆柱形装药如图 4所示。起爆方式采用中心点起爆，通过设定起爆点A、B、C、D、E、F、G、H、I、J的10种起爆方案来研究起爆点位置对子EFP成型的影响，每种方案起爆点之间相隔10 mm。对起爆点距离药型罩轴向距离为0，10，20，30，40，50，60，70，80，90 mm的10种情况分别进行数值模拟。其中网栅直径d=1 mm，网栅间距L固定为8 mm。

图 4(Fig. 4)

图 4 成型装药结构及起爆点分布 Fig.4 Formed charge structure and initiation point layout

表 5为经网栅切割后的子EFP速度数值模拟结果，由表 5可见，随着起爆点与药型罩顶点轴向距离的增加，MEFP子弹丸径向平均速度(V₁为t=117 μs时刻子EFP的径向平均速度)逐渐减小，当起爆点距离药型罩的轴向距离从0 D_k(D_k为装药口径)增加到1 D_k时，轴向平均速度(V₂为t=117 μs时刻子EFP轴向平均速度)提高了27%，原因是：主装药中心点J起爆药型罩受到的爆轰压力峰值远大于药型罩顶点A起爆受到的爆轰压力峰值^[6]，使得J点起爆所形成的子EFP径向平均速度和轴向平均速度较A点起爆大。

表 5(Tab. 5)

表 5 经网栅切割后的子EFP速度数值模拟结果 Tab. 5 Numerical result of the sub-explosively formed projectile velocity after being cutted No. L1/mm V1/m·s-1 V2/m·s-1 1 0 326.6 1627 2 10 318.3 1644 3 20 307.1 1667 4 30 300.9 1703 5 40 285.9 1747 6 50 268.4 1802 7 60 258.7 1866 8 70 248.6 1931 9 80 243.7 1997 10 90 237.5 2058 Note: L1，the initiation point position；V1，radial velocity of sub-explosively formed projectile when t=117 μs；V2，axial radial velocity of sub-explosively formed projectile when t=117μs.

表 5 经网栅切割后的子EFP速度数值模拟结果 Tab.5 Numerical result of the sub-explosively formed projectile velocity after being cutted

图 5为碰撞网栅前药型罩的压垮过程，由图 5可见，顶点A起爆爆轰波最大压力区较大，药型罩多个微元同时被压垮，因此罩体头尾速度差较小。中心点J起爆药型罩在12 μs时爆轰压力瞬间增大，而且球面波首先传到药型罩顶端，引起翻转后的罩体头尾速度差较大。这导致了中心点J起爆药型罩经网栅切割之后形成的中心子EFP较顶点A起爆走得远。

图 5(Fig. 5)

图 5 碰撞网栅前药型罩的压垮过程 Fig.5 Collapse process of the charge liner before touching the cutting reseau

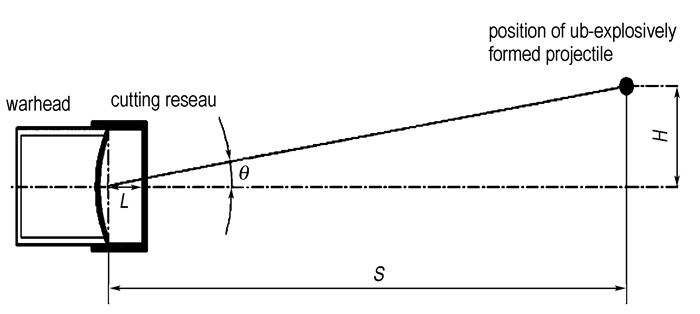
图 6为子EFP发散角示意图，由图 6可见，经网栅切割之后所形成的子EFP发散角为$ \theta = \arctan \frac{H}{S} $，式中, S为战斗部球缺形药型罩端口与子EFP飞行位置之间的水平距离，H为子弹丸的发散半径。

图 6(Fig. 6)

图 6 子EFP发散角示意图 Fig.6 Sketch map of the radial dispersion angle of sub-explosively formed projectile (L the cutting reseau distance; θ, the radial dispersion angle of MEFP; H, the distribution radius of sub-explosively formed projectile; S, the horizontal distance between liner and flying position of sub-explosively formed projectile)

表 6为起爆点位置变化对子EFP发散角影响数值模拟结果，由表 6可见，随着起爆点与药型罩顶点距离的增加，子EFP发散角逐渐减小。模拟表明：起爆点与药型罩顶点距离的变化影响MEFP子弹丸的速度和散布面积，是影响子EFP成型的因素之一。随着起爆点与药型罩顶点距离增加，子EFP径向平均速度逐渐减小，从而导致子EFP的飞行发散角减小。产生这一趋势的原因是：随着起爆点距离的增加，药型罩受到的爆轰压力峰值逐渐增大，造成翻转后的罩体头尾速度差增大，切割后所形成的子EFP头尾仍然存在速度梯度，所以继续产生轴向拉伸，子弹丸向罩轴线闭合而产生径向压缩。所以，药型罩在轴向拉伸、径向压缩的作用下产生发散角。可见，起爆点距离的减小有利于增大子EFP的发散角。

表 6(Tab. 6)

表 6 起爆点位置变化对子EFP发散角影响因素数值模拟结果 Tab. 6 Numerical results of the influence of initiation point position on radial dispersion angle No. L1/mm θ/(°) 1 0 (0.00 Dk) 4.809 2 10 (0.11 Dk) 4.021 3 20 (0.22 Dk) 3.598 4 30 (0.33 Dk) 3.444 5 40 (0.44 Dk) 3.214 6 50 (0.56 Dk) 2.967 7 60 (0.67 Dk) 2.812 8 70 (0.78 Dk) 2.665 9 80 (0.89 Dk) 2.506 10 90 (1.00 Dk) 2.418 Note: L1，the initiation point position；θ，the radial dispersion angle.

表 6 起爆点位置变化对子EFP发散角影响因素数值模拟结果 Tab.6 Numerical results of the influence of initiation point position on radial dispersion angle

当起爆点距离很小时，虽然所形成的子EFP的发散角很大，但速度较低，毁伤目标的能力弱。起爆点距离过大虽然使得子EFP的速度有所提高，侵彻目标能力增强，但导致了MEFP子弹丸发散角减小，散布面积缩小。所以，起爆点距离的过大或过小都会使得药型罩错过了最佳的切割时机，从而影响子EFP的侵彻能力。因此，起爆点距离应在一个适当的范围内变动，并存在一个最佳值。模拟表明：起爆点距离在0.56 D_k(起爆点距药型罩顶点的轴向距离为50 mm)到0.89 D_k(起爆点距药型罩顶点的轴向距离为80 mm)范围内能形成理想的子EFP, 且在0.78 D_k(起爆点距药型罩顶点的轴向距离为70 mm)时子EFP具有良好的气动力外形和较高的侵彻速度。

(1) 在圆环形网栅切割式MEFP成型的数值模拟中，采用流固耦合算法可有效克服拉格朗日算法模拟炸药爆轰过程中所产生的网格畸变这一缺点，提高了数值模拟结果的准确性。利用圆环形切割网栅可以在原来的单个EFP装药结构的基础上产生5个具有一定威力和方向性的子EFP, 能够用于攻击轻型装甲目标。为多模战斗部的设计工作打下了基础。

(2) 通过数值模拟研究了单点起爆位置对子EFP成型的影响，得出当起爆点距离药型罩的轴向距离从0 D_k增加到1 D_k，子EFP轴向平均速度提高27%。

(3) 分析了起爆点位置这一因素对子EFP发散角的影响，可以采用适当减小起爆点距离的方法来增大子EFP的散布面积，从而提高MEFP的命中概率。起爆点距离的增减对子EFP的速度变化有明显的影响。起爆点距离在0.56 D_k到0.89 D_k范围内能形成理想的子EFP, 且在0.78 D_k时子EFP具有良好的气动力外形和较高的侵彻速度。