咪唑类化合物及其衍生物在医药[1]、农药[2]、生物无机化学[3]和含能材料[4-7]等方面具有广泛的应用。4,5-二(1H-四唑-5-基)-1H-咪唑(H3BTI)是一种结构新颖的咪唑衍生物,其4, 5位为四唑取代基,氮含量为68.61%,是一种典型的唑类高氮化合物,分解产物中氮气含量较高,在低特征信号推进剂或气体发生剂等领域具有潜在的应用前景。2008年,Mircea Dinca等人[8]首次合成出了H3BTI,并以其为配体,通过与氯化钴在碱性条件下的自组装反应获得了一种具有混合价态的新型钴配合物。2009年,Min Guo[9]报道了H3BTI的晶体中具有丰富的氢键作用,预示着该化合物具有较好的热稳定性。目前尚未见文献报道H3BTI的热性能研究, 为此,本研究优化了H3BTI的合成工艺,并利用DSC和TG/DTG技术研究了H3BTI的热分解行为,采用非等温DSC技术研究了H3BTI的热分解动力学,为其在含能材料领域的应用提供了基础。
2 实验部分 2.1 试剂与仪器试剂:4,5-二氰基咪唑(DCI)为工业品,叠氮化钠、氯化铵、盐酸和N, N-二甲基甲酰胺(DMF)等均为分析纯。
仪器:美国热电尼高力公司NEXUS870型傅里叶变换红外光谱仪、德国Exementar公司VARI-EL-3型元素分析仪、瑞士Bruker公司AV500型(500 MHz)超导核磁共振仪、日本岛津DSC-60型差示扫描光谱仪、STA449C型热分析仪。
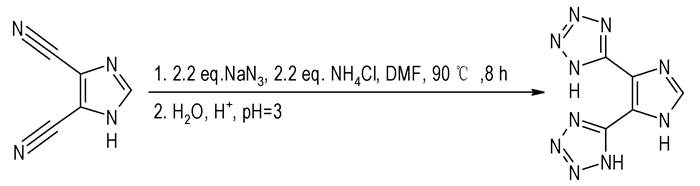
2.2 实验过程室温下, 将4,5-二氰基咪唑(0.01 mol)溶于30 mL N, N-二甲基甲酰胺中,加入叠氮化钠(0.024 mol)和氯化铵(0.024 mol),油浴加热至90 ℃,恒温反应8 h。减压蒸出DMF,将剩余固体分散在200 mL水中,滴加10%的盐酸溶液调节溶液pH值至3,滤出白色固体后经水洗和干燥,得产物4,5-二(1H-四唑-5-基)-1H-咪唑半水合物,收率94.6%。合成路线如Scheme 1所示。
|
Scheme1 Synthesis of H3BTI |
1H NMR (DMSO-d6, 500 MHz), δ: 8.25。13C NMR (DMSO-d6, 125 MHz), δ: 121.58, 139.36, 149.32。IR(KBr, cm-1), ν: 3427, 3160, 3016, 2768, 2649, 1869, 1634, 1571, 1514, 1464, 1423, 1329, 1281, 1243, 1199, 1161, 1072, 1008, 956, 888, 747, 645。Anal. Calcd for C5H4N10·0.5H2O: C, 28.17; H, 2.36; N, 65.71; Found: C, 28.21; H, 2.20; N, 65.49。
3 结果与讨论 3.1 合成工艺优化Mircea Dinca等人[8]采用体积比为4:1的甲苯和甲醇混合液作为反应溶剂,三乙胺盐酸盐为催化试剂,回流反应3 d,收率93.5%,反应周期较长。Min Guo[9]以DMF为反应溶剂,氯化铵为催化试剂,但其物料比无法保证原料完全反应。通过分析上述两种方法的优缺点,对H3BTI的合成工艺进行优化,采用稍过量(2.2倍量)的叠氮化钠与氯化铵和4,5-二氰基咪唑在DMF中, 于温度90 ℃的条件下反应8 h,以94.6%的较高收率获得H3BTI,结果见表 1。
| 表 1 H3BTI的合成方法 Tab.1 Synthetic methods of H3BTI |
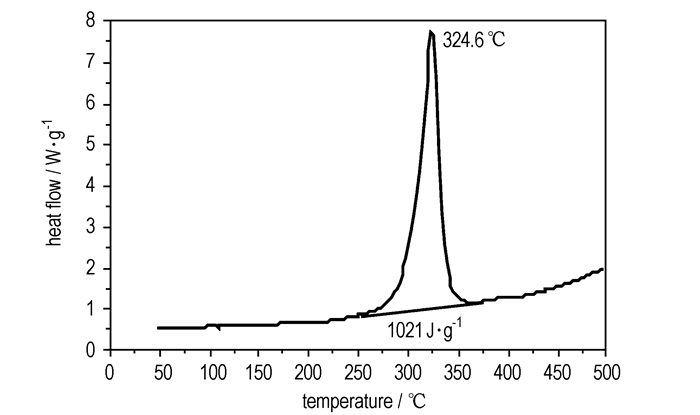
采用DSC对H3BTI的热性能进行研究(升温速率10 K·min-1),结果如图 1所示。由图 1可见,DSC曲线中未发现明显的吸热峰,表明该化合物无明显的熔化过程,这与熔点测试过程未发现样品熔化,仅发生颜色变化一致。324.6 ℃时有一个明显的放热峰,对DSC曲线进行积分计算后得知它的分解热约为208 kJ·mol-1,表明H3BTI在该温度发生了剧烈的放热分解反应。DSC曲线上无明显熔化过程,说明该放热峰为H3BTI的固相分解过程。热重曲线如图 2所示,由图 2可见,最大分解速率温度为337.5 ℃,至374.6 ℃时,质量损失为42.32%,表明该化合物具有较好的热稳定性。
|
图 1 H3BTI的DSC曲线 Fig.1 DSC curve of H3BTI |

|
图 2 H3BTI的TG曲线 Fig.2 TG curve of H3BTI |
表 2为不同加热速率2.5,5.0,10.0, 15.0 K·min-1下DSC曲线的主放热峰和由此获得的初始反应温度(Te)及峰顶温度(Tp);表 3为由DSC曲线得到的热力学数据。为了揭示H3BTI放热分解的反应机理,获得其最概然机理函数和相应的动力学参数,对表 2中的主放热峰、初始反应温度(Te)和峰顶温度(Tp)以及表 3中的基本数据,采用如下6种动力学分析方法进行计算,其中包括1种微分方程(方程(1))和5种积分法(方程(2)~(6)):
Kissinger法[10]
| $ \ln \frac{{{\beta }_{\text{i}}}}{T_{\text{Pi}}^{2}}=\ln \frac{{{A}_{\text{K}}}R}{{{E}_{\text{K}}}}-\frac{{{E}_{\text{K}}}}{R{{T}_{\text{Pi}}}},\text{i}=1\tilde{\ }4,\left( {{E}_{\text{K}}}\ \text{in}\ \text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}} \right) $ | (1) |
Flann-Wall-Ozawa法[11]
| $ \lg \beta = \lg \left[ {\frac{{A{E_0}}}{{RG\left( \alpha \right)}}} \right] - 2.315 - 0.4567\frac{{{E_0}}}{{RT}},\left( {{E_0}\;{\rm{in}}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{{\rm{ - 1}}}}} \right) $ | (2) |
Mac Callum-Tanner法[12]
| $ \lg [G\left( \alpha \right)] = lg\left( {\frac{{A{E_{\rm{a}}}}}{{\beta R}}} \right) - 0.4828E_{\rm{a}}^{0.4357} - \frac{{0.449 + 0.217{E_a}}}{{0.001T}},\left( {{E_{\rm{a}}}\;{\rm{in}}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{{\rm{ - 1}}}}} \right) $ | (3) |
Satava-Sestak法[13]
| $ \lg [G\left( \alpha \right)] = lg\left( {\frac{{A{E_{\rm{a}}}}}{{\beta R}}} \right) - 2.315 - 0.4567\frac{{{E_{\rm{a}}}}}{{RT}},\left( {{E_{\rm{a}}}\;{\rm{in}}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) $ | (4) |
Agrawal法[14]
| $ \lg [\frac{{G\left( \alpha \right)}}{{{T^2}}}] = lg\left[ {\frac{{AR}}{{\beta {E_{\rm{a}}}}}\left( {\frac{{1 - \frac{{2RT}}{{{E_{\rm{a}}}}}}}{{1 - \frac{{5RT}}{{{E_{\rm{a}}}}}}}} \right)} \right] - \frac{{{E_{\rm{a}}}}}{{RT}},\left( {{E_{\rm{a}}}\;{\rm{in}}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) $ | (5) |
一般积分法[15]
| $ \lg [\frac{{G\left( \alpha \right)}}{{{T^2}}}] = lg\left[ {\frac{{AR}}{{\beta {E_{\rm{a}}}}}\left( {1 - \frac{{2RT}}{{{E_{\rm{a}}}}}} \right)} \right] - \frac{{{E_{\rm{a}}}}}{{RT}},\left( {{E_{\rm{a}}}\;{\rm{in}}\;{\rm{kJ}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}} \right) $ | (6) |
上述方程中,α=Ht/H0,为反应深度,Ht为H3BTI在某时刻的反应热,H0为总放热量,T为绝对温度,Ea为表观活化能,A为指前因子,G(α)为积分机理函数,β为升温速率,R为通用气体常数。
从表 2结果可见,由Kissinger方法计算的表观活化能193.66 kJ·mol-1和由Flann-Wall-Ozawa方法计算的表观活化能193.40 kJ·mol-1基本一致,且线性相关系数都接近于1,表明计算结果可信,并以此作为检验其他计算方法一致性的标准。同时,由表观活化能值可知,H3BTI的稳定性较好。
将不同升温速率下的DSC数据Ti和αi(i=1,2,3…)列于表 3,然后分别代入Flann-Wall-Ozawa方程中,得到不同转化率时的活化能变化曲线,如图 3所示。由图 3可知,当α= 0.25~0.85时,表观活化能变化较小,因此,选用此范围的α计算H3BTI的非等温反应动力学参数。
| 表 2 多重扫描速率法计算所得H3BTI热分解反应的动力学参数 Tab.2 Kinetic parameters of the exothermic decomposition reaction of H3BTI obtained by the multiple heating methods |
| 表 3 由DSC曲线得到的热力学数据 Tab.3 Thermodynamics results from DSC curves |

|
图 3 H3BTI在不同分解深度的Ea-α曲线 Fig.3 Ea-α curve of H3BTI at different decomposition extents |
将表 3中α在0.25~0.85之间对应的数据α、β及T与41种机理函数[16]分别代入到方程(3)~(6),由线性最小二乘法求得41种机理函数在相应升温速率β下各自对应的Ea、A、线性相关系数r、标准偏差SD及可信因子d(d=(1-r)SD),并依据如下判断依据[17]确定最概然机理函数:
(1) 80 kJ·mol-1<Ea<250 kJ·mol-1,7 s-1<lgA<30 s-1;
(2) r>0.98;
(3) SD<0.30;
(4) 微、积分法所得Ea和lgA的值应大致相近,并尽量与Flann-Wall-Ozawa法结果一致;
(5) Ea对应的机理函数形式与样品状态相符。满足该条件的机理函数为15号函数G(α)=[-ln(1-α)]3/4,由其计算所得热力学参数结果列于表 4中。可见,由此机理函数计算所得不同升温速率下的E和lgA值呈现一定的偏差,其平均值与Kissinger法和Flann-Wall-Ozawa法所得结果基本一致。
| 表 4 H3BTI的热分解反应动力学参数计算结果 Tab.4 Calculated values of kinetic parameters of thermal decomposition reaction for H3BTI |
因此H3BTI热分解的最概然机理函数的积分式G(α)=[-ln(1-α)]3/4,相应微分式f(α)=4/3(1 -α)[-ln(1-α)]1/4。表明H3BTI的热分解反应受随机成核和随后生长控制,反应机理服从n=3/4的Avrami-Erofeev方程。因此,H3BTI的热分解动力学参数为Ea=197.62 kJ·mol-1,lgA=16.16。
将最概然机理函数的微分式及所求得的Ea、lgA代入方程(7)中,得到H3BTI热分解反应的动力学方程为式(8)所示。
| $ \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \left( {\frac{A}{\beta }} \right)f\left( \alpha \right){e^{-\frac{E}{{RT}}}} $ | (7) |
| $ \frac{{{\rm{d}}\alpha }}{{{\rm{d}}T}} = \frac{{1.927}}{\beta } \times {10^{16}}\left( {1- \alpha } \right){[-ln\left( {1-\alpha } \right)]^{\frac{1}{4}}}{e^{ -\frac{{2.377 \times {{10}^4}}}{T}}} $ | (8) |
为了考察H3BTI由放热分解导致热爆炸的行为,获得其热爆炸临界温度值(Tbe和Tbp),将表 2中βi、Tei及Tpi,i=1~4,代入方程(9)[18],得β→0时的Te0和TP0值分别为543.07,569.05 K。
| $ {T_{\left( {{\rm{e}}\;{\rm{or}}\;{\rm{p}}} \right)}} = {T_{\left( {{\rm{e0}},{\rm{or}},{\rm{p0}}} \right)}} + b{\beta _i} + c\beta _i^2,i = 1 \sim 4 $ | (9) |
| $ {T_{{\rm{be}}\;{\rm{or}}\;{\rm{bp}}}} = \frac{{{E_0}-\sqrt {E_0^2-4{E_0}R{T_{{\rm{e0}}\;{\rm{or}}\;{\rm{p0}}}}} }}{{2R}} $ | (10) |
式中,Te为外推始点温度,K;Tp为热分解峰温,K;Te0,Tp0分别为当β →0时对应的Te和Tp时的温度,K;β为升温速率,K·min-1;b和c分别为系数。
利用方程(10)[17]计算得H3BTI的临界爆炸温度为Tbe=556.38 K,Tbp=583.70 K。其中Tbe>Tbe(RDX)=487.90 K[19],表明其热稳定性优于RDX。
当T=Tp0,Ea=Ek,A=Ak时,可由式(11)~(13)得到峰温处热分解反应的活化熵、活化焓和活化自由能分别为35.72 J·mol-1·K-1、193.66 kJ·mol-1及173.33 kJ·mol-1。
| $ A = \frac{{{k_B}T}}{h}{e^{\Delta S \ne /R}} $ | (11) |
| $ A\exp \left( {-\frac{E}{{RT}}} \right) = \frac{{{k_B}T}}{h}\exp \left( {\frac{{\Delta {S^ \ne }}}{R}} \right)\exp \left( {\frac{{-\Delta {H^ \ne }}}{{RT}}} \right) $ | (12) |
| $ \Delta {G^ \ne } = \Delta {H^ \ne }-T\Delta {S^ \ne } $ | (13) |
式中,kB为波尔兹曼常数,1.3807×10-23 J·K-1;h为普朗克常数,6.626×10-34 J·s
4 结论用优化的工艺完成了H3BTI的合成,4,5-二氰基咪唑、叠氮化钠和氯化铵的摩尔比为1:2.2:2.2, 溶剂为DMF, 反应温度90 ℃, 反应时间8 h, 收率达到94.6%。以DSC和TG/DTG技术研究了H3BTI的热分解性能,结果表明,H3BTI无熔化过程,324.6 ℃时的放热峰为固相分解过程,分解热约为208 kJ mol-1。以不同升温速率的DSC技术,研究了H3BTI的非等温反应动力学,研究结果表明,热分解反应受随机成核和随后生长控制,反应机理服从n=3/4的Avrami-Erofeev方程,热分解反应的动力学方程为
| [1] |
高学军, 李庆章. 广谱抗蠕虫药物奥芬达唑研究进展[J].
动物医学进展, 2004, 25(3): 53-55. GAO Xue-jun, LI Qing-zhang. The progress of study on oxfendazole[J]. Progress In Veterinary Medicine, 2004, 25(3): 53-55. |
| [2] |
许诚, 丁秀丽, 李宗英, 等. 杀菌剂氰霜唑的合成与表征[J].
应用化工, 2009, 38(7): 1076-1077, 1083. XU Cheng, DING Xiu-liu, LI Zong-ying, et al. Synthesis and characterization of fungicide cyazofamid[J]. Applied Chemical Industry, 2009, 38(7): 1076-1077, 1083. |
| [3] |
蒋宗林, 肖蓉, 苏晓渝, 等. 咪唑衍生物的一锅法选择性合成[J].
高等学校化学学报, 2003, 24(1): 64-67. JIANG Zong-lin, XIAO Rong, SU Xiao-yu, et al. Selective one-pot synthetic method for imidazole and benzimidazole derivatives[J]. Chemical Journal of Chinese Universities, 2003, 24(1): 64-67. |
| [4] |
杨国臣, 刘慧君, 曹端林. 4,5-二硝基咪唑的制备[J].
含能材料, 2006, 14(5): 349-351. YANG Guo-chen, LIU Hui-jun, CAO Duan-lin. Prepration of 4,5-dinitroimidazole[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2006, 14(5): 349-351. |
| [5] |
杨威, 姬月萍. 多硝基咪唑及其衍生物的研究进展[J].
火炸药学报, 2008(5): 46-50. YANG Wei, JI Yue-ping. Progress in polynitroimidazoles and derivatives[J]. Chinese Joumal of Explosives and Propellants, 2008(5): 46-50. |
| [6] |
杨利, 高福磊, 凡庆涛, 等. 咪唑类含能化合物的研究进展[J].
含能材料, 2009, 17(3): 374-379. YANG LI, GAO Fu-lei, FAN Qing-tao, et al. Progress in imidazolium-based energetic compounds[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(3): 374-379. |
| [7] |
杨威, 王伯周, 姬月萍, 等. 1-甲基-2, 4,5-三硝基咪唑(MTNI)的热分解动力学及机理研究[J].
含能材料, 2012, 20(2): 176-179. YANG Wei, WANG Bo-zhou, JI Yue-ping, et al. Thermal decomposition kinetics and mechanism of 1-methyl-2, 4,5-trinitroimidazole[J]. Chinese Journal of Energetic Materials(Hannene Cailiao), 2012, 20(2): 176-179. |
| [8] |
Dinca M, Harris T D, Iavarone A T, et al. Synthesis and characterization of the cubic coordination cluster[Co6ⅢCo2Ⅱ(IBT)12]]14- (H3IBT = 4,5-bis(tetrazol-5-yl)imidazole)[J].
Journal of Molecular Structure, 2008, 890(1-3): 139-143. DOI:10.1016/j.molstruc.2008.03.048 |
| [9] |
Guo M. 4,5-Bis(1H-tetrazol-5-yl)-1H-imidazole monohydrate[J].
Acta Crystallographica, 2009, 65(6): o1403 |
| [10] |
Kissnger H E. Reaction kinetics in differential thermal analysis[J].
Anal Chem, 1957, 29(11): 1702-1706. DOI:10.1021/ac60131a045 |
| [11] |
Ozawa T. A new method of analyzing thermogravimetric data[J].
Bul Chem Soc Jpn, 1965, 38: 1881-1886. DOI:10.1246/bcsj.38.1881 |
| [12] |
MacCallum J R, Tanner J. The kinetics of thermogravimetry[J].
Eur Polymer J, 1970, 6(7): 1033-1039. DOI:10.1016/0014-3057(70)90035-2 |
| [13] |
Škvára F, Šesták J. Computer calculation of the mechanism and associated kinetic data using a non-isothermal integral method[J].
J Therm Anal, 1975, 8(3): 477-489. DOI:10.1007/BF01910127 |
| [14] |
Agrawal R K. A new equation for modeling nonisothermal reactions[J].
J Therm Anal, 1987, 32(1): 149-156. DOI:10.1007/BF01914557 |
| [15] |
Coats A W, Redfern J P. Kinetic parameters from thermogravimetric Data[J].
Nature, 1964, 201: 68-69. DOI:10.1038/201068a0 |
| [16] |
胡荣祖, 史启祯.
热分析动力学[M]. 北京: 科学出版社, 2001: 127-131.
HU Rong-zu, SHI Qi-zhen. Thermal analysis kinetics[M]. Beijing: Science Press, 2001: 127-131. |
| [17] |
Hu R, Yang Z, Ling Y. The determination of the most probable mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a[J].
Thermochim Acta, 1988, 123: 135-151. DOI:10.1016/0040-6031(88)80017-0 |
| [18] |
Zhang T, Hu R, Xie Y, et al. The estimation of critical temperatures of thermal explosion for energetic materials using non-isothermal DSC[J].
Thermochim Acta, 1994, 244: 171-176. DOI:10.1016/0040-6031(94)80216-5 |
| [19] |
徐抗震, 常春然, 宋纪蓉, 等. RDX的比热容、热力学性质及绝热至爆时间[J].
火炸药学报, 2008, 31(4): 35-38. XU Kang-zhen, CHANG Chun-ran, SONG Ji-rong, et al. Specific heat capacity, thermodynamic properties and adiabatic time to-explosion of RDX[J]. Chin J Explos Propel, 2008, 31(4): 35-38. |
The synthetic technology of 4,5-bis(1H-tetrazol-5-yl)-1H-imidazole(H3BTI) was optimized with yield up to 94.6%. Furthermore, the thermal behavior and non-isothermal decomposition kinetics of H3BTI were studied by DSC and TG/DTG method.




