2. 中国兵器工业集团第051基地,陕西 华阴 714200
2. China Ordnance Industry No.051 Base, Huayin 714200, China
高氯酸铵/端羟基聚丁二烯(ammonium perchlorate/hydroxyl-terminated polybutadiene,AP/HTPB)是一种综合性能优良的复合固体推进剂,被应用于榴弹的底排增程技术。AP/HTPB底排药柱首先在火炮膛内被高温高压燃气点燃,弹丸出炮口后,药剂的燃烧环境由炮口压力迅速下降到大气压,将经历燃烧失稳、熄灭、复燃(在点火具作用下)的强非稳态燃烧,二次点火不一致将导致底排弹射程散布较普通榴弹偏大[1]。陆春义等人[2-3]采用内腔尺寸与底排装置相同的半密闭爆发器进行了大量模拟实验,研究了AP/HTPB底排推进剂在高降压速率条件下的瞬变燃烧特性。张领科等人[4-5]曾对底排装置在膛内的燃烧特性以及飞行工作期间的内流场进行了分析。本工作研究底排模拟装置燃烧室在瞬态泄压工况下内流场的变化特性。通过建立底排燃烧室内流场的二维轴对称非稳态模型,数值模拟获得底排燃烧室内各流动参数在瞬态泄压过程中的分布特性。
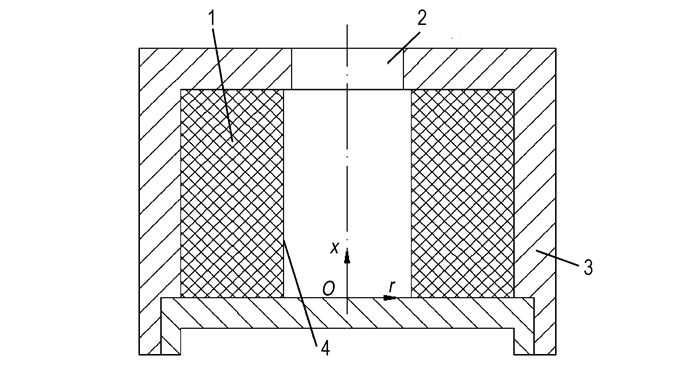
2 物理模型某底排燃烧室结构示意图如图 1所示,根据底排弹装药结构及瞬态过程的特点,提出如下基本假设:(1)一般AP/HTPB底排药柱为单孔三侧缝结构,为便于建立二维轴对称模型,将内孔表面积乘以一个系数对药柱燃烧面积进行修正;(2)底排药柱燃烧遵循几何燃烧定律,且考虑快速降压对燃速的影响;(3)燃烧过程在燃烧表面极薄层内迅速完成,向燃烧室内添加具有某种热力学性质与输运性质的燃气;(4)将燃气视为理想气体,忽略其体积力、浮力等次要因素的影响;(5)泄压前底排药柱已达稳定燃烧状态,燃烧室内为高温高压环境;(6)由于瞬态泄压过程非常短暂,可忽略热散失。
|
图 1 底排燃烧室结构示意图 1—复合底排药柱,2—排气孔,3—燃烧室壳体,4—燃烧表面 Fig.1 Structural sketch of base bleed combustion chamber 1—composite base bleed propellant grain, 2—exhaust nozzle, 3—combustion chamber shell, 4—burning surface |
根据上述物理模型,建立二维轴对称非稳态数学模型。
3.1 燃烧室内流场控制方程(1) 质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r\rho v} \right)}}{{\partial r}} = 0 $ | (1) |
(2) 动量守恒方程
| $ \frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho uu} \right)}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r\rho uv} \right)}}{{\partial r}} = \frac{{\partial {P_{{\rm{xx}}}}}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r{P_{{\rm{xr}}}}} \right)}}{{\partial r}} $ | (2a) |
| $ \frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho vu} \right)}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r\rho vv} \right)}}{{\partial r}} = \frac{{\partial {P_{{\rm{rx}}}}}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r{P_{{\rm{rr}}}}} \right)}}{{\partial r}} $ | (2b) |
(3) 能量守恒方程
| $ \begin{array}{l} \frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho Eu} \right)}}{{\partial X}} + \frac{1}{r}\frac{{\partial \left( {r\rho Ev} \right)}}{{\partial r}}\\ = \frac{\partial }{{\partial X}}\left( {u{P_{{\rm{xx}}}} + v{P_{{\rm{xr}}}} + \lambda \frac{{\partial T}}{{\partial X}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r \cdot \left( {u{P_{{\rm{rx}}}} + v{P_{{\rm{rr}}}} + \lambda \frac{{\partial T}}{{\partial r}}} \right)} \right] \end{array} $ | (3) |
(4) 状态方程
| $ p = \rho {R_{\rm{g}}}T $ | (4) |
其中,应力张量的各分量分别为:
| $ {P_{{\rm{xx}}}} =-p + 2\mu \left( {\frac{{\partial u}}{{\partial x}}-\frac{1}{3}\nabla \cdot \mathop V\limits^ \to } \right) $ | (5a) |
| $ {{\mathop{\rm P}\nolimits} _{{\rm{rr}}}} =-p + 2\mu \left( {\frac{{\partial v}}{{\partial r}}-\frac{1}{3}\nabla \cdot \mathop V\limits^ \to } \right) $ | (5b) |
| $ {P_{{\rm{xr}}}} = {P_{{\rm{rx}}}} = \mu \left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial r}}} \right) $ | (5c) |
式中,x和r分别为轴向和径向坐标,m;u和v分别为轴向速度和径向速度,m·s-1;ρ为燃气密度,kg·m-3;E为总能,J·kg-1;T为温度,K;λ为导热系数,W·(m·K)-1;p为压力,Pa;Rg为气体常数,J·(kg·K)-1;μ为粘性系数,kg·(m·s)-1;柱坐标系下的速度散度为:
| $ \nabla \cdot \mathop V\limits^ \to = \frac{{\partial u}}{{\partial x}} + \frac{1}{r}\frac{{\partial rv}}{{\partial r}} $ | (6) |
采用k-ε两方程模型描述湍流运动,其二维轴对称形式[6]为:
| $ \begin{array}{l} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho uk} \right)}}{{\partial x}} + \frac{1}{r}\frac{{\partial \left( {r\rho vk} \right)}}{{\partial r}}\\ \;\;\;\;\;\;\;\;\;\; = \frac{\partial }{{\partial x}}\left( {\frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}\frac{{\partial k}}{{\partial x}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}\frac{{\partial k}}{{\partial r}}} \right) + G - \rho \varepsilon \end{array} $ | (7) |
| $ \begin{array}{l} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho u\varepsilon } \right)}}{{\partial x}} + \frac{1}{r}\frac{{\partial \left( {r\rho v\varepsilon } \right)}}{{\partial r}}\\ \;\;\;\;\;\;\;\; = \frac{\partial }{{\partial x}}\left( {\frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial x}}} \right) + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial r}}} \right) + {c_1}G\frac{\varepsilon }{k} - {c_2}\rho \frac{{{\varepsilon ^2}}}{k} \end{array} $ | (8) |
其中,G表示由于平均速度引起的湍动能生成项
| $ G = {\mu _{\rm{t}}}\left\{ {2\left[{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial r}}} \right)}^2} + {{\left( {\frac{v}{r}} \right)}^2}} \right] + {{\left( {\frac{{\partial u}}{{\partial r}} + \frac{{\partial v}}{{\partial x}}} \right)}^2}} \right\} $ | (9) |
式中,k为湍动能,J·kg-1;ε为湍流耗散率,J·(kg·s)-1;湍流粘性系数μ t=cμρk2/ε,kg·(m·s)-1;常数cμ =0.09,c1=1.44,c2=1.92,σk=1.0,σε=1.3。
3.3 燃速模型考虑降压速率对底排推进剂燃速的影响,采用线燃速修正公式[7]如下:
| $ \mathop {{\rm{ }}r}\limits^. = \mathop {{r_0}}\limits^. \left( {1 + \frac{{\varphi n\alpha }}{{{{\mathop {{r_0}}\limits^. }^2}P}} \cdot \frac{{{\rm{d}}p}}{{{\rm{d}}t}}} \right) $ | (10) |
底排推进剂单位燃烧面积上的质量流量为:
| $ \mathop m\limits^. /(\beta A) = {\rho _{\rm{c}}} \cdot \mathop r\limits^. $ | (11) |
式中,
由于是轴对称问题,取图 1中燃烧室与排气孔的一半流动通道及底排燃烧室外部适当的大气空间作为计算域,模型的边界条件有燃烧表面、对称轴、壁面和压力出口。根据燃面质量通量平衡可得:
| $ {\rho _{\rm{g}}} \cdot {v_{\rm{g}}} = {\rho _{\rm{c}}} \cdot \mathop r\limits^. $ | (12) |
式中,ρ g为燃气密度,kg·m-3;vg为燃气流动速度,m·s-1;方向垂直于燃烧表面。
压力出口边界条件为
| $ p = p\left( t \right) $ | (13) |
初始条件为
| $ p = {p_0}, \rho = {\rho _0}, T = {T_0}, u = {u_0}, v = {v_0} $ | (14) |
根据所建立的物理模型和数学模型,利用FLUENT软件,对底排燃烧室在瞬态泄压工况下的燃烧流场特性进行数值计算,其中,燃烧模块根据本研究的数理模型编制,嵌入到FLUENT软件中。针对文献[3]的实验条件,即泄压前底排燃烧室内初始压力p0=56 MPa,温度T0=1812 K,进行数值模拟。计算所需的相关参数[8]如表 1所示。
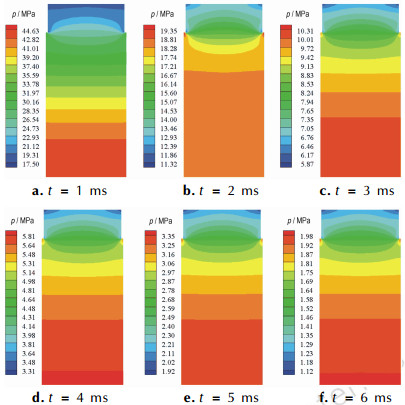
4.1 底排燃烧室内压力分布在泄压过程中底排燃烧室内的压力分布云图如图 2所示。可以看出,在泄压过程中,压力在轴向上的变化非常明显,而在径向上分布比较均匀,燃面附近的压力与轴线上的压力差别很小。在靠近排气孔处,由于流动通道突然收缩,在台阶前后产生了两处明显的高压区和低压区,在台阶下方的一段燃烧室内,压力在轴线处最低,沿径向升高;而在台阶上方的喷孔内,压力在轴线处最高,沿径向降低。
|
图 2 不同时刻底排燃烧室内压力分布 Fig.2 Pressure distribution in base bleed combustion chamber at different instants |
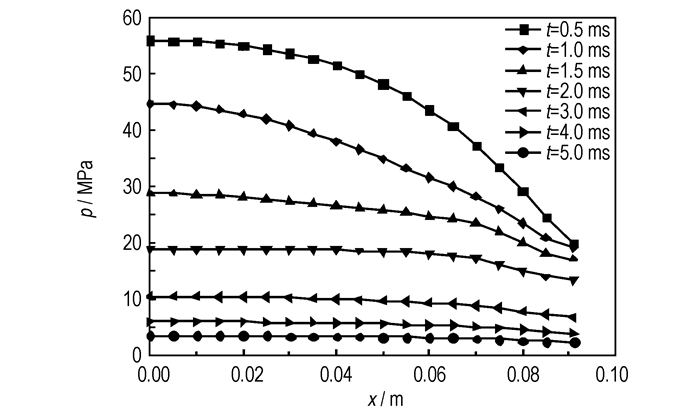
为便于分析泄压过程中压力分布的详细变化规律,图 3给出了不同时刻底排燃烧室轴线上的压力分布。在瞬态泄压前期,燃烧室轴线上最大压力与最小压力相差较大,燃烧室内燃气流动迅速发展,降压速率非常高。随着时间推移,轴线上各点的压力逐渐下降,但前端的降压速率高于后端的降压速率。随着压力下降,轴线上各点的压力分布趋于均匀,燃气流动变得平稳,由于排气孔内外压差减小,降压速率大幅降低。
|
图 3 不同时刻底排燃烧室轴线上压力分布 Fig.3 Pressure profile on the axis of base bleed combustion chamber at different instants |
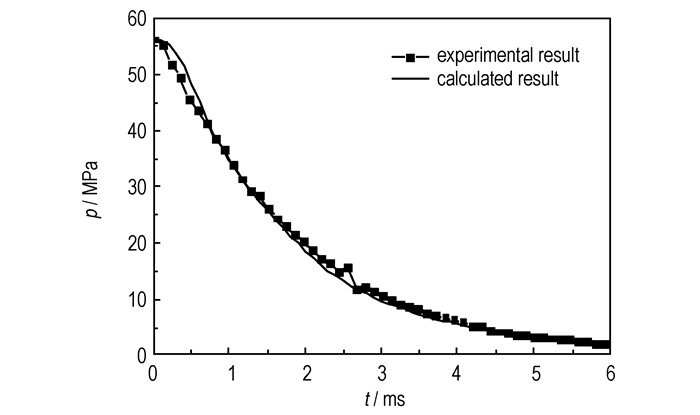
瞬态泄压过程中底排模拟装置轴线上x=0.04 m处p-t曲线的计算值与文献[3]实测值的对比如图 4所示,可见两者吻合较好。
|
图 4 底排燃烧室内压力的计算值与实测值的比较 Fig.4 Comparison of calculated and experimental pressures in base bleed combustion chamber |
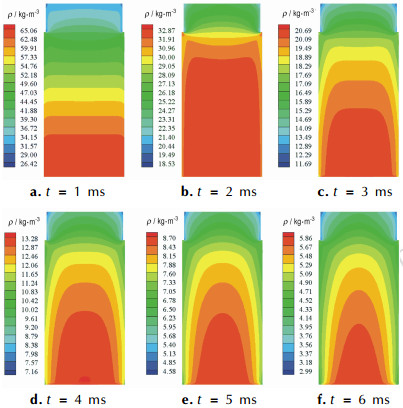
为了考查燃面附近底排推进剂燃气的加入对底排燃烧室燃烧流场特性的影响,图 5和图 6分别给出了瞬态泄压过程中燃烧室内的密度和温度分布。可以看出,由于底排推进剂燃烧表面向燃烧室内喷入高温燃气,燃烧室内密度和温度均呈现明显的二维分布。随着燃烧室内压力下降,密度和温度沿轴向不断降低,其下降速率也随之降低。密度由泄压前期在径向截面大部分区域的均匀分布,逐步发展为轴线处最高、沿径向逐渐降低的单峰分布;而泄压过程中温度在同一径向截面上则沿径向升高。形成这种分布的原因是底排推进剂燃气的“添质加能”作用:底排推进剂燃烧向燃烧室内喷入高温燃气,使得燃面附近温度高于轴线处温度,而高温燃气的“添质”作用相对于“加能”较弱,且随泄压向外排出,因此燃面附近密度较低。
|
图 5 不同时刻底排燃烧室内密度分布 Fig.5 Density distribution in base bleed combustion chamber at different instants |
|
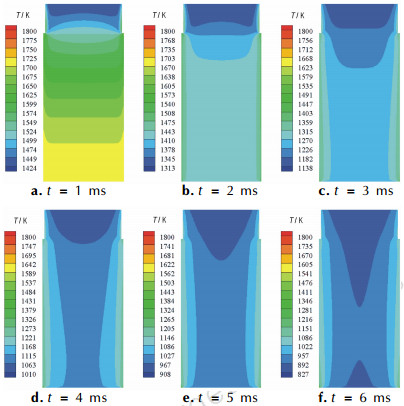
图 6 不同时刻底排燃烧室内温度分布 Fig.6 Temperature distribution in base bleed combustion chamber at different instants |
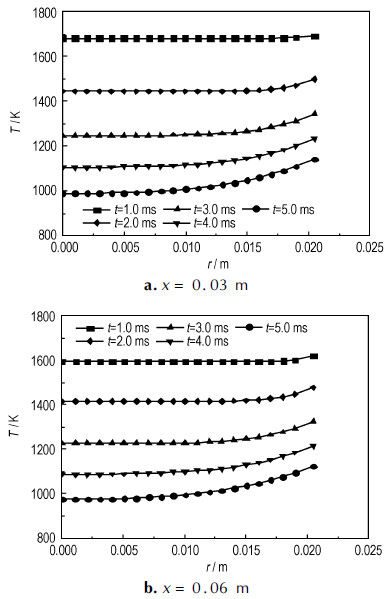
图 7为燃烧室内x=0.03 m和x=0.06 m两截面上径向温度随时间的变化。由图可见,当t=1.0 ms时,燃烧室内温度较高,底排推进剂燃气的“加能”作用对燃烧室内温度分布的影响范围较小;当t=3.0 ms时,底排推进剂燃气的影响范围已比较明显。随着底排燃烧室内压力下降,底排推进剂燃气的“加能”作用越来越显著。对比图 7a和图 7b可以看出,由于燃气向排气孔外流动,在同一时刻,x=0.03 m截面上径向温度分布高于x=0.06 m截面上的相应值。以r=0.01 m处温度为例,当t=2.0 ms时,x=0.03 m和x=0.06 m两个截面上该处温度差ΔT大约为30 K,当t=3.0 ms时,ΔT=23 K,当t=4.0 ms时,ΔT=19 K,说明随着压力下降,轴向上不同位置的温度差异逐渐减小。由于燃气在底排燃烧室内的流动过程中自身内能转化为动能,轴向温度差异减小意味着轴向上气体流速之间的差异减小,即轴向上气体流速变化趋于平缓。
|
图 7 不同轴向位置处径向温度随时间的变化 Fig.7 Radial temperature vs. time at different axial positions |
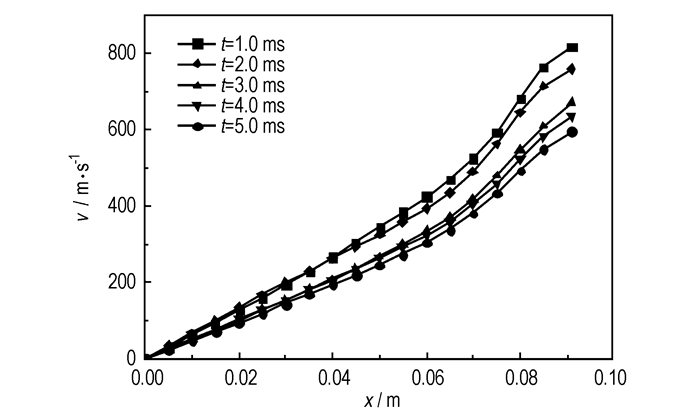
模拟得到的瞬态泄压过程中底排燃烧室内的速度分布云图在等值线轮廓上比较接近,仅在数值上变化明显,而且在轴向上的变化非常剧烈,而在径向上变化不大。因此,此处仅给出了不同时刻轴线上的速度分布,如图 8所示。可以看出,在轴线上x=0.07 m之前燃气流速基本呈线性分布,之后,流动通道由较宽的燃烧室突然收缩为较窄的排气孔,燃气流速加速升高。在降压前期,由于燃烧室内压力非常高,燃气经过膨胀在排气孔出口截面上的流速接近当地音速(模拟结果显示最大马赫数为0.98)。随着压力下降,轴线上各点流速逐渐降低,流动趋于平稳。由于排气孔内外压差减小,排气孔出口处燃气流速不断降低,由1 ms时的816.7 m·s-1降为5ms时的594.3 m·s-1。
|
图 8 不同时刻底排燃烧室轴线上速度分布 Fig.8 Velocity profile on the axis of base bleed combustion chamber at different instants |
(1) 考虑底排推进剂非稳态燃烧,建立了底排模拟装置在瞬态泄压工况下的流动模型,得到的燃烧室内p-t曲线的计算值与实测值吻合较好。
(2) 在泄压过程中,底排燃烧室内压力、密度和温度沿轴向降低,燃气流速沿轴向升高;各流动参数的变化梯度随泄压而减小。
(3) 底排推进剂燃气的加入导致底排燃烧室内密度沿径向降低,而温度沿径向升高,并且随着压力下降,底排推进剂燃气的加能作用变得明显。
(4) 通过对底排模拟装置在瞬态泄压工况下的燃烧流场建模,获取内流场的瞬态变化规律,有利于研究底排弹出炮口泄压瞬间燃烧失稳,寻求控制底排推进剂燃烧不稳定性的方法。
| [1] |
张炎清, 赵子华. 底排弹射击密集度的试验研究[J].
弹道学报, 1991(1): 48-54. ZHANG Yan-qing, ZHAO Zi-hua. An experimental study on the dispersion of the base bleed projectiles[J]. Journal of Ballistics, 1991(1): 48-54. |
| [2] |
陆春义, 周彦煌, 余永刚. 高降压速率下复合底排推进剂瞬变燃烧特性研究[J].
含能材料, 2007, 15(6): 587-591. LU Chun-yi, ZHOU Yan-huang, YU Yong-gang. Combustion of composite base bleed charge under rapid depressurization[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2007, 15(6): 587-591. |
| [3] |
陆春义. 底排装置强非稳态燃烧特性研究[D]. 南京: 南京理工大学, 2009.
|
| [4] |
张领科, 余永刚, 陆欣, 等. 炮膛内底排装置燃烧特性计算分析[J].
兵工学报, 2011, 32(5): 526-531. ZHANG Ling-ke, YU Yong-gang, LU Xin, et al. Calculation and analysis on the combustion characteristics of a base bleed unit in the gun bore[J]. Acta Armamentarii, 2011, 32(5): 526-531. |
| [5] |
张领科, 周彦煌, 陆欣, 等. 某底排弹底排装置工作期间内部流场的数值模拟[J].
含能材料, 2010, 18(2): 217-221. ZHANG Ling-ke, ZHOU Yan-huang, LU Xin, et al. Numerical simulation of interior flow field in a base bleed unit during working[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2010, 18(2): 217-221. |
| [6] |
武晓松, 陈军, 王栋, 等.
固体火箭发动机工作过程数值仿真[M]. 北京: 高等教育出版社, 2006.
WU Xiao-song, CHEN Jun, WANG Dong, et al. Numerical Simulations of Working Progress of Solid Rocket Engine[M]. Beijing: Higher Education Press, 2006 |
| [7] |
Kuo K K, Summerfield M.
Fundamentals of solid propellant combustion[M]. Beijing: China Astronautics Press, 1994 |
| [8] |
郭锡福.
底部排气弹外弹道学[M]. 北京: 国防工业出版社, 1995.
|

A 2D-axisymmetric unsteady model for the combustion flow field in base bleed unit was established. The flow characteristics under transient pressure-release were studied through numerical simulation.



