2. 西北工业大学理学院,陕西 西安 710072
2. School of Natural and Applied Sciences Northwestern Polytechnical University, Xi′an 710072, China
关于炸药冲击起爆过程的实质,目前受到关注较多的是热点理论[1-3],它主要包括炸药晶体的绝热压缩机制和绝热剪切机制,这两种机制均与炸药晶体颗粒的力学性能密切相关,因此评价晶体颗粒的力学性能对于研究炸药的安全性能和起爆性能有着重要意义。但由于炸药晶体颗粒粒径的分散性以及尺寸等因素的限制,采用常规的实验手段测定其模量和强度等力学性能参数存在难以克服的困难。因此,寻求新研究方法成为有效评价炸药晶体颗粒力学性能的关键。
自1957年Alder[4]首次进行分子动力学模拟(Molecular Dynamics simulation, MD)以来,因其在宏观性质计算上具有较高的准确度和有效性,在火炸药研究领域的应用日趋广泛[5-7],其中的一个研究热点即为模拟研究炸药晶体的力学性能,已取得了一些有意义的结论[8-12]。但从相关文献报道看,目前对炸药晶体力学性能的分子动力学研究均为纯粹的模拟仿真,并没有与其宏观力学性质表现联系在一起,导致模拟结果的有效性很难验证,也使得分子动力学方法在实际中应用存在一定的局限性。为此,本研究选择目前广泛应用于混合炸药和固体推进剂等复合含能材料之中的硝胺炸药——RDX和HMX,将分子动力学模拟和撞击加载实验相结合,从炸药晶体在撞击加载下的主要响应——破碎特性的角度,验证炸药晶体力学性能的分子动力学模拟结果,研究分子动力学方法模拟计算炸药晶体力学性能的有效性,以期为该方法评价炸药晶体的力学性能提供参考。
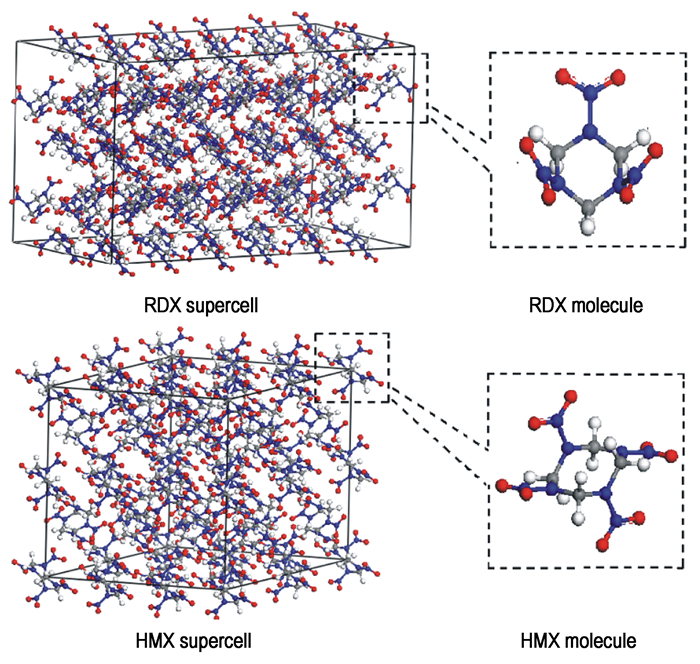
2 实验部分 2.1 分子动力学模拟 2.1.1 模型建立及MD模拟细节由美国Accelrys公司开发的Materials Studio 4.0软件中的visualizer模块,依据RDX和β-HMX晶体衍射数据[13-14],构建RDX和HMX超晶胞(3×2×2),其模型见图 1。利用smart minimizer方法对RDX和HMX晶体模型进行能量优化后,运用discover模块和COMPASS [15]力场,在298 K、1.01×105 Pa条件下,采用Andersen控温方法和Parrinello控压方法对RDX和HMX晶体模型进行300 ps、时间步长为1 fs的NPT(正则系综,系统的粒子数N、压强P和温度T 恒定)分子动力学模拟。其中分子起始速度由Maxwell-Boltzmann随机分布给定,Velocity Verlet算法进行求解。对分子间的范德华和静电作用力计算分别采用atom-based和Ewald方法,非键截取半径0.95 nm,样条宽度(spline width)取0.1 nm,缓冲宽度(buffer width)取0.05 nm。后100 ps体系已经平衡(温度和能量随时间的变化率小于5%),每200 fs取样一次,记录模拟轨迹,对其进行静态力学性能分析。
|
图 1 RDX和HMX的晶体模型 Fig.1 Crystals models of RDX and HMX |
反映小变形条件下弹性体应力与应变关系的广义Hooke定律[16]为:
| $ \left[\begin{array}{l} {\sigma _x}\\ {\sigma _y}\\ {\sigma _z}\\ {\tau _{yz}}\\ {\tau _{xz}}\\ {\tau _{xy}} \end{array} \right] = \left[\begin{array}{l} {C_{11}}\;\;\;{C_{12}}\;\;\;{C_{13}}\;\;\;{C_{14}}\;\;\;{C_{15}}\;\;\;{C_{16}}\\ {C_{21}}\;\;\;{C_{22}}\;\;\;{C_{23}}\;\;\;{C_{24}}\;\;\;{C_{25}}\;\;\;{C_{26}}\\ {C_{31}}\;\;\;{C_{32}}\;\;\;{C_{33}}\;\;\;{C_{34}}\;\;\;{C_{35}}\;\;\;{C_{36}}\\ {C_{41}}\;\;\;{C_{42}}\;\;\;{C_{43}}\;\;\;{C_{44}}\;\;\;{C_{45}}\;\;\;{C_{46}}\\ {C_{51}}\;\;\;{C_{52}}\;\;\;{C_{53}}\;\;\;{C_{54}}\;\;\;{C_{55}}\;\;\;{C_{56}}\;\;\;\\ {C_{61}}\;\;\;{C_{62}}\;\;\;{C_{63}}\;\;\;{C_{64}}\;\;\;{C_{65}}\;\;\;{C_{66}} \end{array} \right]\left[\begin{array}{l} {\varepsilon _x}\\ {\varepsilon _y}\\ {\varepsilon _z}\\ {\gamma _{yz}}\\ {\gamma _{xz}}\\ {\gamma _{xy}} \end{array} \right] $ |
材料的应力是应变的线性组合,其线性组合系数为应变各方向应力分量——弹性系数Cij(i, j=1~6)的矩阵,原则上材料的所有力学性能均可从它的弹性系数矩阵得到。由于应变能的存在,有Cij=Cji,即矩阵对称,因此对于极端各向异性体,只有21个独立的弹性系数。随着物体对称性的提高,独立的弹性系数减少,对各向同性体,只有两个独立的弹性系数C11和C12,令C12=λ,C11-C12=μ,则:
| $ \left[{{C_{ij}}} \right] = \left[\begin{array}{l} \lambda + 2\mu \;\;\;\;\;\;\lambda \;\;\;\;\;\;\;\;\;\;\lambda \;\;\;\;\;\;\;\;\;\;0\;\;\;\;0\\ \;\;\;\lambda \;\;\;\;\;\;\;\;\lambda + 2\mu \;\;\;\;\;\lambda \;\;\;\;\;\;\;\;\;\;0\;\;\;\;0\\ \;\;\;\lambda \;\;\;\;\;\;\;\;\;\;\;\lambda \;\;\;\;\;\;\;\lambda + 2\mu \;\;\;\;\;0\;\;\;\;0\\ \;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\mu \;\;\;\;0\\ \;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\mu \\ \;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;0\;\;\;\;0 \end{array} \right] $ |
λ和μ称为拉梅系数,材料在拉伸、剪切和压缩情况下应力与应变的比值,即拉伸模量E、剪切模量G和体积模量K,以及泊松比γ均可用λ和μ表示:
| $ E = \frac{{\mu \left( {3\lambda + 2\mu } \right)}}{{\lambda + \mu }}, G = \mu, K = \lambda + \frac{2}{{3\mu }}, \gamma = \frac{\lambda }{{2(\lambda + \mu )}} $ |
利用模拟计算所得体系的分子动力学平衡运动轨迹,Materials Studio软件对其进行形变量为0.05%的拉伸与纯切形变操作,然后分析模型并计算可得μ、E、G、K和γ等力学性能参数。
2.2 撞击实验 2.2.1 材料与仪器原材料:RDX和HMX均为E级,由甘肃银光化学工业集团有限公司提供。
仪器:WL-1型立式落锤仪,西安近代化学研究所;Mastersizer 2000型激光粒度仪,英国马尔文仪器公司;FEI QUANTA 600型环境扫描电子显微镜(ESEM),美国FEI公司。
2.2.2 实验方法撞击实验:用WL-1型立式落锤仪,在落锤高度为12.6 cm和质量为(5±0.005)kg的条件下,分别撞击RDX和HMX晶体,测试方法参照GJB-772A-1997,然后收集撞击后的样品,进行粒度测定和扫描电镜观察。
晶体粒度分布测定:利用Mastersizer 2000型激光粒度仪,分析撞击实验前后RDX和HMX晶体的粒度分布,以及比表面积变化情况;测定前利用超声波对RDX和HMX晶体进行分散处理。
晶体微观形貌结构分析:利用FEI QUANTA 600型环境扫描电子显微镜,观察撞击实验前后RDX和HMX晶体的形貌结构变化,实验电压为10 kV,高真空模式。
3 结果与讨论 3.1 力学性能分析经MD模拟、静态力学分析所得RDX和HMX晶体的弹性系数和模量等力学性能参数见表 1,未列入表中的弹性系数的数值均等于或接近于零;同时,表 1中还给出了RDX和HMX晶体弹性系数和模量的实验值。由表 1可知,对于RDX和HMX晶体的力学性能,采用不同的测试方法其实验结果差别较大,而本文对RDX和HMX晶体力学性能的模拟是在同样的力场、参数和计算方法下进行,能够剔除样品状态和测试条件等内外因素对结果的影响,因此从评价RDX和HMX晶体力学性能差异性的角度来讲,虽然模拟计算值较实验值系统性地偏小,但模拟计算结果仍具有相对比较的意义。
| 表 1 RDX和HMX晶体的弹性系数及模量 Tab.1 Elastic constants and modulus of RDX and HMX crystals |
从表 1中的模拟结果可以看出,与RDX相比,HMX晶体弹性系数的 C11、C22、C33组,C44、C55、C66 组和C12、C13、C23组内数值一致性较好,表明其力学性能更加接近各向同性。比较RDX和HMX晶体弹性系数和各模量数值大小可知,HMX晶体在不同受力情况下抵抗弹性形变的能力与RDX相比更强,即其刚性更大,而塑性更小。体模量与剪切模量的比值K/G表示材料塑性变化范围的大小,与材料的延展性成正比关系,因此由表 1中模拟值可看出,RDX晶体的延展性好于HMX,后者的脆性更强;此外,RDX和HMX晶体的泊松比γ均在0.2~0.3之间,属于塑料的范围。
在材料的弹性系数中,C12只与张应力有关,C44只与切应力有关,材料的脆性断裂和韧性断裂分别由张应力和切应力引起。当C12大于C44时,材料易发生剪切形变,切应力很快达到并超过抗剪强度,从而发生韧性断裂,这种情况下材料的延展性较好;当C12小于C44时,材料易发生拉伸形变,张应力很快达到并超过抗拉强度,从而发生脆性断裂,这种情况下材料的脆性较强,因此可用C12-C44(柯西压,Cauchy)评估材料的延展性和脆性。从表 1中模拟值可以看出,虽然RDX晶体的C12小于C44,柯西压为负值,但其数值(-0.215)接近于0,表明RDX晶体虽然呈现脆性,但并不显著;相比之下,HMX晶体的柯西压远小于RDX,相差达到一个数量级,表明HMX晶体的脆性远远强于RDX。因此,可以推断在相同加载条件下,RDX的延展性更好,而HMX晶体呈现的脆性更加显著。
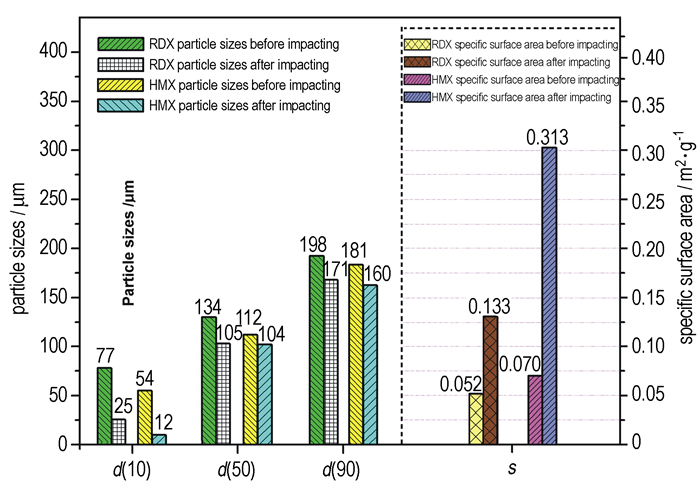
3.2 撞击响应特性分析为了验证3.1中模拟计算结果的有效性,设计了一组撞击加载实验,用落锤分别撞击RDX和HMX晶体,然后通过激光粒度仪和扫描电镜分析撞击前后RDX和HMX的晶体粒度分布、比表面积变化和微观形貌结构变化情况,结果见图 2和图 3。
|
图 2 RDX和HMX晶体的粒度分布和比表面积 Fig.2 The particle size distribution and specific surface area of RDX and HMX crystals |

|
图 3 撞击加载前后RDX和HMX晶体的微观形貌结构 Fig.3 The microcosmic structure of RDX and HMX crystals before and after impacting load |
由图 2可知,撞击后RDX和HMX晶体的粒径均有所降低,尤其是粒径分布中10%所对应的粒径,由77 μm和54 μm分别降低至25 μm和23 μm,降低幅度与50%和90%所对应的粒径相比非常显著,表明两种炸药晶体在撞击后均发生了明显的破碎,粒径减小的同时产成大量的小颗粒碎晶。此外,根据图 2中比表面积的变化情况,不仅可以看出两种炸药晶体产成了破碎现象,而且还可比较出RDX和HMX晶体破碎程度的大小。如RDX晶体比表面积由0.052增大至0.133,增幅为156%;而HMX晶体比表面积由0.070增大至0.313,增幅为347%,HMX晶体的破碎程度明显大于RDX。
从图 3可以看出,在撞击加载后,RDX和HMX晶体的微观形貌结构均产生了明显的变化,但二者的破碎特性存在显著差异。RDX晶体加载前呈较为规整的多面体颗粒状,而加载后呈“片”状结构,表面分布有明显的裂纹,且周围伴随碎晶颗粒存在;表明RDX晶体在撞击加载下以塑性形变为主,同时发生脆性断裂。与RDX晶体相比,HMX晶体虽然也有呈现“片”状结构的趋势,但其程度不如RDX晶体,而且脆性断裂的表现更为明显,表面可观察到“山峦”状晶体破碎痕迹。
由上述实验结果可知,在相同撞击加载条件下,RDX晶体的延展性较好,而HMX晶体的脆性较强,这与本文3.1中模拟计算结果的分析结论相一致。
4 结论(1) 分子动力学模拟结果表明,与RDX相比,HMX的弹性系数、拉伸模量(E)、体模量(K)、剪切模量(G)和柯西压较大,而K/G值较小,这预示RDX晶体的延展性更好,而HMX晶体的脆性更加显著。
(2) 撞击加载实验结果表明,RDX和HMX晶体在撞击后均发生了明显的破碎,且HMX晶体的破碎程度更加显著;RDX晶体以塑性形变为主,同时发生脆性断裂,其延展性较好;HMX晶体脆性断裂的表现更为明显,其脆性较强。
(3) 通过与RDX和HMX晶体撞击加载响应的实验结果比较,发现分子动力学方法用于评价不同炸药晶体力学性能之间差异性具有较高的准确度和有效性。
| [1] |
Campbell A W, Davis W C, Travis J R. Shock initiation of detonation in liquid explosives[J].
Phys Fluids, 1961, 4(4): 498-508. DOI:10.1063/1.1706353 |
| [2] |
Field J E. Hot spot ignition mechanisms for explosives[J].
Accounts of Chemical Research, 1992, 25(11): 489-496. DOI:10.1021/ar00023a002 |
| [3] |
Armstrong R W, Ammon H L, Elban W L, et al. Investigation of hot spot characteristics in energetic crystals[J].
Thermochimica Acta, 2002, 384(1-2): 303-313. DOI:10.1016/S0040-6031(01)00786-9 |
| [4] |
Alder B J, Wainwright T E. Phase transition for a hard sphere system[J].
Journal of Chemical Physics, 1957, 27: 1208-1209. DOI:10.1063/1.1743957 |
| [5] |
朱伟平. 分子模拟技术在高分子领域的应用[J].
塑料科技, 2002, 151(5): 23-25, 33. ZHU Wei-ping. Application of Molecular Simulation Technology to Macromolecule[J]. Plastics Science and Technology, 2002, 151(5): 23-25, 33. |
| [6] |
齐晓飞, 张晓宏, 宋振伟, 等. 分子动力学方法在火炸药研究中的应用进展[J].
化学推进剂与高分子材料, 2012, 57(3): 41-46. QI Xiao-fei, ZHANG Xiao-hong, SONG Zhen-wei, et al. Application progress of molecular dynamics method in propellants and explosives[J]. Chemical Propellants & Polymeric Materials, 2012, 57(3): 41-46. |
| [7] |
陈正国, 朱申敏, 程时远. 分子模拟方法及在高聚物中的应用[J].
材料导报, 1997, 11(6): 49-51. CHEN Zheng-guo, ZHU Shen-ming, CHENG Shi-yuan. Molecular simulation methods and its applications in polymer[J]. Materials Review, 1997, 11(6): 49-51. |
| [8] |
Sewell T D, Menikoff R, Bedrov D, et al. A molecular dynamics simulation study of elastic properties of HMX[J].
The Journal of Chemical Physics, 2003, 119: 7417-7426. DOI:10.1063/1.1599273 |
| [9] |
肖继军, 黄辉, 李金山, 等. HMX晶体和HMX/F2311PBXs力学性能的MD模拟研究[J].
化学学报, 2007, 65(17): 1746-1750. XIAO Ji-jun, HUANG Hui, LI Jin-shan, et al. MD simulation study on the mechanical properties of HMX crystals and HMX/F2311PBXs[J]. Acta Chimica Sinica, 2007, 65(17): 1746-1750. DOI:10.3321/j.issn:0567-7351.2007.17.002 |
| [10] |
石一丁, 黄风雷. 不同温度下β -HMX状态方程的分子动力学模拟[J].
北京理工大学学报, 2010, 30(7): 854-857. SHI Yi-ding, HUANG Feng-lei. Molecular dynamics simulation of isothermal equations of state of β -HMX at different temperatures[J]. Transactions of Beijing Institute of Technology, 2010, 30(7): 854-857. |
| [11] |
石一丁, 黄风雷. HMX状态方程与弹性性能的分子动力学研究[J].
含能材料, 2009, 17(5): 562-567. SHI Yi-ding, HUANG Feng-lei. Molecular dynamics simulation of isotherm and elastic properties of HMX[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(5): 562-567. |
| [12] |
朱伟, 肖继军, 马秀芳, 等. 不同温度下RDX晶体力学性能的MD模拟[J].
火炸药学报, 2007, 30(4): 17-19. ZHU Wei, XIAO Ji-jun, MA Xiu-fang, et al. Molecular dynamics simulation of elastic properties on RDX crystal at different temperatures[J]. Chinese Journal of Explosives & Propellants, 2007, 30(4): 17-19. |
| [13] |
Choi C S, Prince E. The crystal structure of cyclotrimethylenetrinitramine[J].
Acta Cryst, 1972, B28: 2857-2862. |
| [14] |
Cady H H, Larson A C, Cromer D T. The crystal structure of α-HMX and a refinement of the structure of β -HMX[J].
Acta Cryst, 1963, 16: 617-623. DOI:10.1107/S0365110X63001651 |
| [15] |
Sun H, Ren P, Fried J R. The COMPASS force field:parameterization and validation for hosphazenes[J].
Computational and Theoretical Polymer Science, 1998, 8(1-2): 229-246. DOI:10.1016/S1089-3156(98)00042-7 |
| [16] |
吴家龙.
弹性力学[M]. 上海: 同济大学出版社, 1996.
WU Jia-long. Elasticity[M]. Shanghai: Tongji University Press, 1996 |
| [17] |
Schwarz R B, Hooks D E, Dick J J, et al.Resonant ultrasound spectroscopy measurement of the elastic constants of cyclotrimethylene trinitramine[J/OL]. Journal of Applied Physics, 2005, 98(5): 056106-056106-3.
|
| [18] |
Haycraft J J, Stevens L L, Eckhardt C J.The elastic constants and related properties of the energetic material cyclotrimethylene trinitramine (RDX) determined by Brillouin scattering[J/OL]. Journal of Chemical Physics, 2006, 124(2): 024712.
|
| [19] |
Stevens L L, Eckhardt C J. The elastic constants and related properties of β -HMX determined by Brillouin scattering[J/OL]. Journal of Chemical Physics, 2005, 122(17): 174701.
|




