等离子体起爆技术是一种具有高安全和高可靠性的先进起爆技术,受到国内外广泛重视,其中微桥箔是高能等离子体换能元的重要组成部分,起到能量转换的作用,其吸收起爆回路输出的脉冲能量,发生金属电爆炸,电爆炸产生等离子体快速膨胀为后续推动飞片提供动力源[1-2]。因此,研究微桥箔的电爆炸作用过程具有重要意义。
金属电爆炸过程的机制非常复杂,包括两个基本机理:与焦耳热有关的热机理和为磁流体动力学不稳定性发展所决定的“力学”机理[3]。国外研究较早,得到了一些相对成熟的理论模型。1977年Logan等[4]报道了他们对电爆炸箔加热和爆炸现象的试验与计算研究结果,计算使用了有限差分算法。Stanton报道了用于计算爆炸箔特性的一维流体动力学计算编码CHARTD。1987年,美国Los Alamos[5]实验室利用一维磁流体动力学程序CONFUSE对金属箔电爆炸过程进行了数值模拟。现在国外已经发展到用二维结合三维磁流体动力学模型对金属箔电爆炸过程进行模拟[6],可以获得电压、电流、电阻等参数。国内对金属电爆炸模型的研究处于起步探索阶段,大部分工作还是利用外部仪器设备来检测所发生的现象[7-8]。胡晓棉[9]、韩成智[10]等建立了桥箔电爆炸过程的二维模型,但是模型中电阻率的方程采用了简化模型,所以还是一种半经验的模型。虽然国外已经研发出了爆炸箔二维和三维的动力学模型,能通过公式获得其动态参数,但很少从理论上研究电爆炸过程中的温度变化和分布情况。而在电爆炸过程中桥箔的温度是表征电爆炸特性的重要参数,其升温过程可反映桥箔电爆炸动态变化过程,因此,有必要对爆炸箔电爆炸过程的温度分布情况进行研究。导体固体加热阶段为爆炸箔电爆炸的第一个阶段,它对形成等离子体的浓度和时间有着重要的影响,而等离子体是后续推动飞片的动力源,直接影响起爆电流。因此,爆炸箔在加热阶段的电热分析具有重要意义,为理论研究电爆炸过程中的温度变化和分布提供基础。本研究利用有限元方法对铜微桥箔融化前的电热过程进行了分析,同时讨论了输入电流参数对电热过程的影响,对桥箔与脉冲参数的合理匹配具有一定作用。
2 电热方程的无量纲化铜微桥箔在脉冲电流输入下由于焦耳热作用温度升高,在桥区融化前,是电热耦合作用。其热作用可用瞬态热传导方程(1)表示[11],
| $ {c_{\rm{v}}}{\sigma _{\rm{m}}}\frac{{\partial T}}{{\partial t}} = {\sigma _e}|E{|^2} + \nabla \cdot \left( {k\nabla T} \right) $ | (1) |
式中,cv为比热,J·kg-1·K-1;ρm为桥箔密度,kg·m-3;T为温度,K;t为时间,s;σe为电导率,S·m-1;E为电场强度,V·m-1;k为热导率,W·m-1·K-1。铜的比热cv和热导率k是温度的函数,其与温度(T<1500 K) 关系用公式(2)和(3)表示[11]:
| $ {c_{\rm{v}}} = 0.1004T + 355.12 $ | (2) |
| $ k =-0.0685T + 420.75 $ | (3) |
而铜的电阻率ρe与温度的关系为[12]:
| $ {\rho _{\rm{e}}} =-4.12 \times {10^{-10}} + 0.113 \times {10^{-5}}{\left( {T/11604} \right)^{1.145}} $ | (4) |
同时,该过程满足电荷在导体中传输的连续方程[13]:
| $ \nabla \cdot J = E \cdot \nabla {\sigma _{\rm{e}}} + {\sigma _{\rm{e}}}\nabla E = 0 $ | (5) |
式中,J为电流密度,A·m-2。通过求解上述两个方程可对微桥箔在脉冲电流刺激下的电热效应进行分析。将方程组进行无量纲化处理,令:
| $ {t^*} = t/{t_{\rm{p}}} $ | (6) |
| $ {l^*} = l/w $ | (7) |
| $ {T^*} = \left( {T-{T_{{\rm{amb}}}}} \right)/\left( {{T_{\rm{m}}}-{T_{{\rm{amb}}}}} \right) $ | (8) |
| $ {I^*} = I/{I_{{\rm{max}}}} $ | (9) |
| $ m* = m/\left[{\frac{{I_{\max }^2t_{{\rm{cycle}}}^3}}{{{\sigma _{\rm{e}}}\left( {{T_{{\rm{amb}}}}} \right){w^3}}}} \right] $ | (10) |
式中,tp为输入电流脉冲的周期,s;l为桥区长度,m;w为桥区宽度,m;Tm为桥箔融化温度,K;Tamb为环境温度,K;I为电流,A;Imax为输入电流峰值,A;tcycle为脉冲电流周期,s;上标带*的变量为无量纲量。将其带入控制方程中,有:
| $ {\nabla ^*} = \left( {\frac{\partial }{{\partial x}}i + \frac{\partial }{{\partial y}}i + \frac{\partial }{{\partial x}}k} \right)/\left( {\frac{1}{w}} \right) $ | (11) |
| $ c_{\rm{v}}^* = {c_{\rm{v}}}/\left[{\frac{{{w^2}}}{{\left( {{T_{\rm{m}}}-{T_{{\rm{amb}}}}} \right)t_{{\rm{cycle}}}^2}}} \right] $ | (12) |
| $ \rho _m^* = \rho m/\left[{\frac{{I_{\max }^2t_{{\rm{cycle}}}^3}}{{{\sigma _{\rm{e}}}\left( {{T_{{\rm{amb}}}}} \right){w^6}}}} \right] $ | (13) |
| $ \sigma _{\rm{e}}^* = {\sigma _{\rm{e}}}/{\sigma _{\rm{e}}}\left( {{T_{{\rm{amb}}}}} \right) $ | (14) |
| $ {E^*} = E/\left[{\frac{{I_{\max }^2t_{{\rm{cycle}}}^3}}{{{\sigma _{\rm{e}}}\left( {{T_{{\rm{amb}}}}} \right){w^2}}}} \right] $ | (15) |
| $ {k^*} = k/\left[{\frac{{I_{\max }^2}}{{\left( {{T_{\rm{m}}}-{T_{{\rm{amb}}}}} \right){\sigma _{\rm{e}}}\left( {{T_{{\rm{amb}}}}} \right){w^2}}}} \right] $ | (16) |
式中,x,y,z分别为笛卡尔坐标系的x轴,y轴,z轴;i,j,k分别为x轴,y轴,z轴的单位矢量。
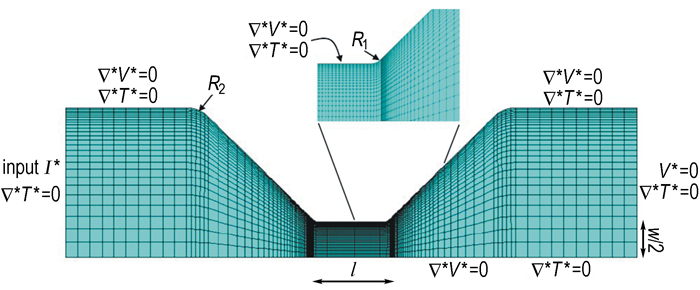
3 电热过程的有限元模型 3.1 桥箔物理结构与基本假设采用有限元分析软件Ansys/Multiphysics对铜微桥箔融化前的电热过程进行模拟。为减少计算量,假设桥箔在厚度方向上材质均匀,则可将问题简化为二维的。由于桥箔为对称结构,取桥箔的上半部分进行分析,图 1所示为微桥箔建模及网格划分示意图,微桥箔的桥区长度和宽度分别l和w,R1和R2分别为0.01 mm和0.5 mm,桥区与连接区的夹角为45°,桥箔总长度和总宽度为9.4 mm和5 mm。
|
图 1 微桥箔网格划分及边界条件示意图 Fig.1 Finite element mesh and boundary conditions of a small scale bridge foil |
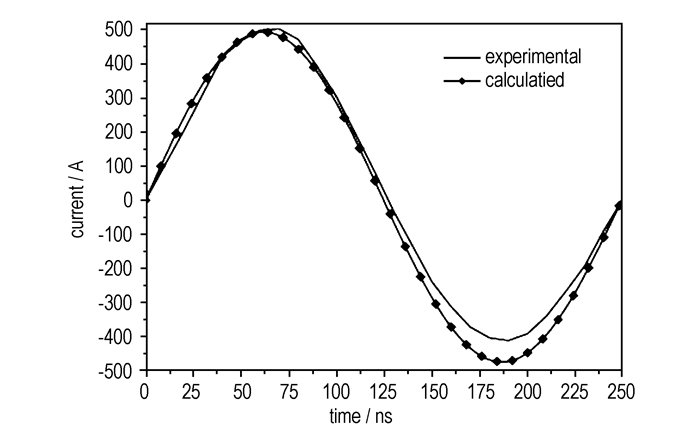
由于铜的热导率与电导率相比存在量级上的差距,因此,可忽略桥箔与环境的热传导,即桥箔边界上有▽*T*=0,具体的边界条件见图 1所示。初始时刻桥区温度为环境温度。桥箔的输入电流I由一个容量C为0.025 μF的电容放电单元施加,该电容放电单元在800 V充电电压条件下的试验所得短路电流波形如图 2所示。
|
图 2 试验短路电流曲线与计算曲线对比 Fig.2 Comparison between the current waveform recorded using current probe and calculated one |
一般地,电容放电回路可视为一个串联RLC电路,根据短路试验结果可以推算回路电感D和电阻R[14]。RLC回路的电流可通过公式(17)计算得到[15-16]:
| $ I\left( t \right) = V/\left[{L\sqrt {\frac{1}{{L \cdot C}}-\frac{{R_{\rm{c}}^2}}{{4{L^2}}}} \sin \left( {\sqrt {\frac{1}{{L \cdot C}}-\frac{{R_{\rm{c}}^2}}{{4{L^2}}}t} } \right){e^{-\frac{{{R_c}}}{{2L}}t}}} \right] $ | (17) |
根据方程(17)计算得到短路电流曲线与试验曲线在第一个半周期内基本一致(图 2),而对于爆炸箔的电热过程以及电爆炸通常只有第一个半周期有效,因此电流输入条件可通过方程(17)从理论上获得。由于将微桥箔负载连入回路后,回路电阻为Rc(t)=R+Rfoil(t),其中,Rfoil为微桥箔电阻,是时间t的函数,相应地,方程(17)中的电阻应为含负载的回路电阻。另外,对于二维电热问题,Ansys默认微桥箔为单位厚度,因此,输入Ansys的电流应乘以一个系数w/tfoil。
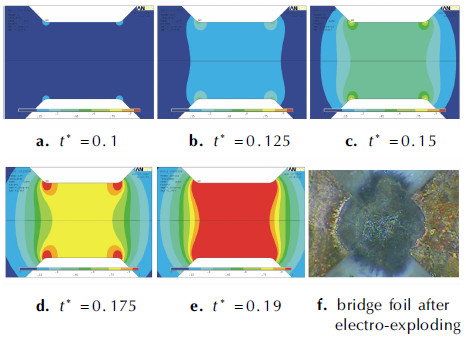
4 论微桥箔电热过程分析与讨论 4.1 脉冲电流刺激下微桥箔桥区温度变化过程对桥区尺寸为100 m×100 m×2 m的铜微桥在图 2所示的脉冲电流作用下的电热过程进行了模拟,桥箔初始电阻约为40 mΩ。图 3所示为不同时刻微桥箔桥区的温度分布情况及铜桥箔电爆炸后桥区显微图。
|
图 3 不同时刻微桥箔桥区的温度分布情况及铜桥箔电爆炸后桥区显微图 Fig.3 Temperature distribution of the small-scale bridge foil at different time steps |
从图 3可以看出,在t*=0.1时,桥区的四个拐点处最早在输入电流的作用下开始升温,但升温并不明显,此时,微桥箔其它区域无明显升温现象。随后,随着输入电流的快速增大,整个桥区范围内的温度由于焦耳热作用迅速升高,而桥区四个拐点处由于温度高于桥区中心区域,其电导率随之有一定幅度降低,电阻较之其它区域高,因此,该处的升温速率进一步增大;同时,由于热传导作用,最早产生温升的桥区边缘温度也向中心扩散,最终在t*=0.19的时候,整个桥区基本完全达到融点。随着电流的持续输入,桥区将有可能发生融化、气化、甚至等离子体化。图 3f是铜桥箔等离子体化后的显微图,可以看出发生爆炸的桥区的形状与模拟桥区的温度梯度基本一致,因此,推测可通过桥区融化前的温度变化研究对桥箔的爆发情况进行预估。另外,若要实现桥区的电爆炸且能量利用率最高,则需要实现桥箔形状和尺寸与输入电流的匹配,最优化的匹配是桥区正好在电流达到峰值时发生电爆炸,而对于桥区尺寸为数百微米的爆炸箔,经验表明桥区融化时间约为爆发时间的90%[17-18],因此,可以通过计算桥区融化所需时间实现桥区参数与输入电流的匹配。通过微桥箔在短脉冲电流作用下的电热分析仅能对电爆炸的过程进行推测,对爆炸箔的指导作用有限,然而,金属电热作用是电爆炸过程的第一步,在电热分析基础上,结合桥箔的融化热,金属电爆炸等离子体的状态方程将能够从理论上实现具有物理意义的电爆炸完整过程的三维模拟,真实的指导爆炸箔的设计。目前,获得准确的等离子体状态方程存在一定难度,然而,随着等离子体流场参数的测试方法日趋精确和多样,如多通道光学高温计[19],粒子图像测速方法[20]、纹影高速摄影技术[21]等,能够促使进一步了解和认识电爆炸产生等离子体的本质,并最终实现电爆炸过程的预测。
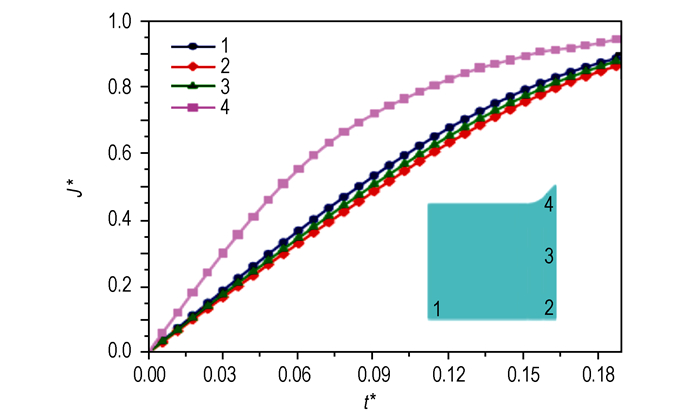
对桥区四个区域的电流密度随时间变化情况进行了分析,如图 4所示。区域1对应于桥区中心,区域4对应于桥区拐点处。
|
图 4 桥区各处电流密度J*随时间变化的曲线 Fig.4 The variation of current density J* with time at different locations |
从图 4可以看出,拐点处的电流密度明显大于其它几个区域,中心处的电流密度稍大于2、3点处的电流密度,而2、3点处的电流密度相差不大。一般地,电子在金属中的运动分为热运动与自由运动,当在铜微桥箔两端施加电压时,每个自由电子都将受到电场力的作用,使电子沿着与场强相反的方向相对于晶格做加速的定向运动。由于整个桥箔范围内电子的热运动矢量平均为零,因此,桥区内的电流密度分布主要与自由电子在电场中的运动相关。电子的漂移速度通常约为10-4 m·s-1,而此处微桥箔的融化时间不足100 ns,因此,电子的运动距离很短,而拐点处由于截面积陡然缩小,导致了拐点处电子聚集,电子数密度较之其它区域非常大,根据J=nev(n为电子数密度,m-2;e为电子所带电荷,C;v为漂移速度,m·s-1)可以判断拐点处的电流密度最大。由于拐点处电子数密度大,该处自由电子与晶体点阵上的原子实碰撞的频率更高,在碰撞时把定向运动能传递给原子实,使之热运动加剧,使得该处的温度快速升高,因此,该处的产生温升最高,并且升温速率也最快,如图 5所示。
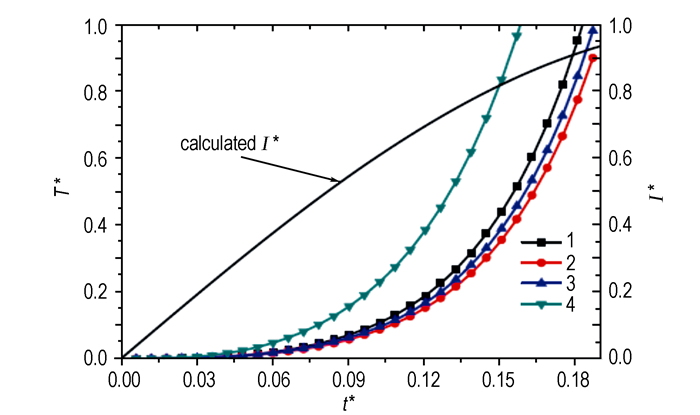
|
图 5 桥区各处温度T*随时间变化的曲线 Fig.5 The variation of temperature T* with time at different locations |
从图 5可以看出,中心处的升温速率及温度较之2, 3处的稍高,这表明热扩散是桥区产生温度梯度的主要原因,并且,热量最初从桥区四个拐点处以圆弧R1圆心为原点,从半径为R1的圆弧开始向四周扩散,因此,可以推断该圆弧的半径对于桥箔的设计是非常重要的。尽管桥区中心处与圆弧R1的距离较之2, 3点稍大,但由于两个圆弧的热量甚至四个圆弧的热量均可扩散至桥区中心处,而2, 3点因热扩散升温则主要依靠与之接近的一个圆弧,这也是为何3处的温度和升温速率高于2处,因此,可以推断在桥箔设计中,桥区的长度也是一个需要重点考虑的参数。
4.2 输入电流对微桥箔电热过程的影响此外,探讨了充电电压对桥区升温速率的影响。一般地,同一电容放电回路的回路电感和电阻不变,即输出电流波形周期长短不随充电电压变化而改变,而对于不同充电电压条件下的输出电流波形,其无量纲化的电流-时间曲线均是一致的,如图 6中计算无量纲电流曲线I *所示。对不同电压输入条件下桥箔的电热过程进行了模拟,图 6所示为不同输入电压条件下微桥箔桥区中心处的温度随时间的变化曲线。

|
图 6 不同电压条件下桥区中心的温度变化曲线 Fig.6 Nodal temperature profiles at the center of small-scale bridge foils under specified input voltages |
从图 6可以看出,在其它条件不变的情况下,随着电压的升高,桥区中心处温度达到融化温度所需的时间逐渐缩短,因此,在进行桥箔能量利用率优化时,充电电压与桥箔之间也存在一定的匹配关系,而不仅仅是放电回路的周期。当电压小于一定值时,放电回路输出的脉冲电流将无法使桥区中心达到融化温度,对于本研究的算例,当充电电压为395 V时,桥区中心温度在半个周期内无法达到桥箔的融点,而当电压降至300V时,无量纲温度T*最大只能达到0.4,其升温速率明显低于400 V时的升温速率,升温速率的急剧降低主要是由于电流较小,前半周期电流上升部分桥箔温度升高缓慢,进而导致电阻增大幅度较之电压为400 V时较小,由此产生的焦耳热变少,因此,升温缓慢。
研究了充电电压对桥区中心处升温至融点(T*=1)所需的时间的影响,计算结果如图 7所示。从图 7可以看出,能够使桥区达到融化温度的临界充电电压约为400 V。输入电压低于临界充电电压时,桥区不能完全达到融化温度;当充电电压略大于临界电压时,tmelt*随电压增大而较大幅度地缩短,而当电压达到800 V时,tmelt*变小的趋势不明显。
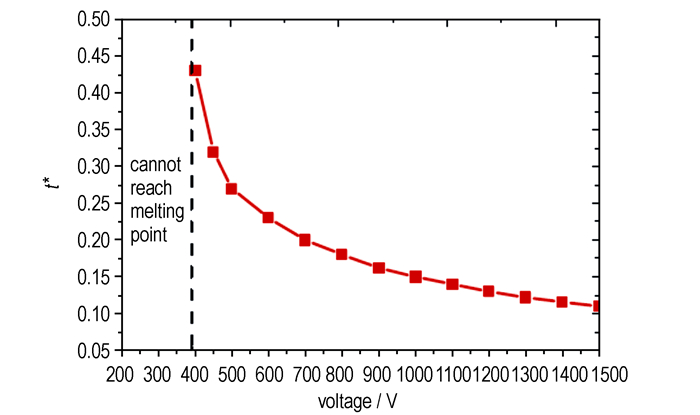
|
图 7 桥区中心升温至融点所需时间tmelt*与充电电压的关系 Fig.7 Relationship between time for the center node of the bridge to reach the melt point and input voltages |
采用容量为0.025 μF的电容放电单元对三种宽度的铜微桥箔进行了爆发电流电压测试,充电电压为800 V,桥区尺寸分别为:20 μm×20 μm×2 μm、40 μm×40 μm×2 μm、60 μm×60 μm×2 μm。图 8为测试得到的桥箔电爆炸过程的流过桥区的电流和桥区两端电压随时间变化的曲线。
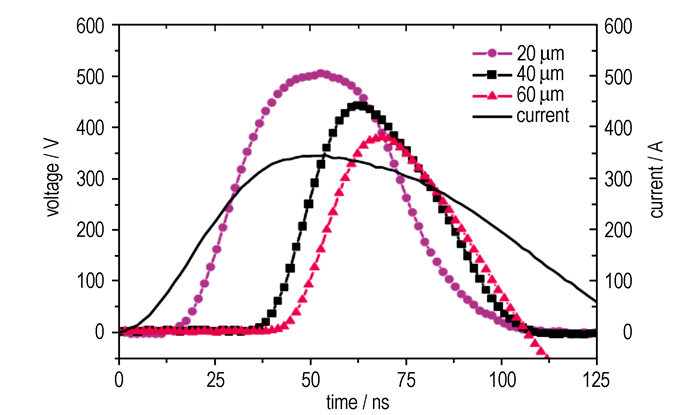
|
图 8 不同桥区宽度微桥箔电爆炸电流电压曲线 Fig.8 The current and voltage profiles of exploding foils that have different bridge width |
根据试验条件,对微桥箔的中心点温度变化情况进行了模拟,进而获得不同宽度同微桥箔达到融化温度所需的时间,结果如图 9所示。

|
图 9 不同宽度微桥箔桥区中心点的温度变化曲线 Fig.9 Nodal temperature profiles at the center of small-scale bridge foils |
通过电流电压曲线可以确定微桥箔的爆发时间,与计算所得的微桥箔桥区中心融化所需时间tmelt进行了对比,见表 1。从表 1可以看出,融化所需时间占爆发时间的比例随铜微桥箔的桥区宽度增大而变大,推测当桥区宽度达到一定值后,达到融化温度所需时间占比例将不再随宽度增加而发生较大变化,即对于数百微米的爆炸箔,其融化时间占爆发时间的比例基本是固定的,与国外学者的研究是吻合的[17-18]。
| 表 1 不同桥区宽度微铜箔的融化所需时间与实测爆发时间对比 Tab.1 Comparison between calculated tmelt and burst time for micro copper foils |
采用有限元方法对脉冲电流刺激下铜微桥箔的电热过程进行了分析,得到如下结论:
(1) 在桥区的四个拐点处升温速率最高,热量从这四个区域向桥区内部扩散。
(2) 在输入脉冲电流周期不变的条件下,随着充电电压的升高,桥区中心处温度达到融化温度所需的时间逐渐缩短。
(3) 存在一个使桥区达到融化的临界电压,当输入电压低于临界充电电压时,桥区不能完全达到融化温度;当充电电压略大于临界电压时,tmelt*随电压增大而较大幅度地缩短,而当电压远大于临界电压时,tmelt*变小的趋势不明显。
(4) 融化所需时间占爆发时间的比例随铜微桥箔的桥区宽度增大而变大,当桥区宽度达到一定值后,达到融化温度所需时间占比例基本不变。
| [1] |
曾庆轩, 袁士伟, 罗承沐. 新型电爆炸箔系统电压对爆发电流影响的实验研究[J].
火工品, 2002(1): 41-42. ZENG Qing-xuan, YUAN Shi-wei, LUO Cheng-mu. Study to the effect of the voltage of a new type of exploding foil initiator system to firing current[J]. Initiators & Pyrotechnics, 2002(1): 41-42. |
| [2] |
成剑, 栗保明. 电爆炸过程导体放电电阻的一种计算模型[J].
南京理工大学学报, 2003, 27(4): 371-375. CHENG Jian, LI Bao-ming. A theoretical model for wire resistance in wire exploding process[J]. Journal of Nanjing University of Science and Technology, 2003, 27(4): 371-375. |
| [3] |
王莹. 电爆炸导体及其应用[J].
爆炸与冲击, 1986, 6(2): 184-192. WANG Yin. The application of exploding conductor[J]. Explosion and Shock Waves, 1986, 6(2): 184-192. |
| [4] |
Logan J D, Lee R S, Weingart R C. Calculation of heating and burst phenomena in electrically exploded foils[J].
J Appl Phys, 1977, 48(2): 621-628. DOI:10.1063/1.323646 |
| [5] |
Lindemuth I R, Brownell J H, Greene A E. Exploding metallic foils for slapper, fuse and hot plasma applications: computational predictions, experimental observations[J].
IEEE Pulsed Power, 1987, 30: 299-305. |
| [6] |
Majalee A, Ikkurthi V R, Chaturvedi P S. Mixed 3-D/2-D simulation of an exploding foil opening switch[J].
IEEE Pulsed Power, 2003, 2: 7803-7815. |
| [7] |
周翔. 用于冲击片雷管的Al/CuO反应含能桥膜研究[D]. 南京: 南京理工大学, 2012.
ZHOU Xiang. Research on Al/CuO-based reactive energetic bridge foils applied in exploding foil initiator[D]. Nanjing: Nanjing University of Science & Technology, 2012. |
| [8] |
Rui Guo, Yan Hu, Ruiqi Shen, et al. A micro initiator realized by integrating KNO3@CNTs nanoenergetic materials with a Cu microbridge[J].
Chemical Engineering Journal, 2012, 211: 31-36. |
| [9] |
韩成智. 电爆炸箔起爆系统作用过程研究[D]. 北京: 北京理工大学, 2006.
HAN Chen-zhi. Study on process of exploding foil initiation system[D]. Beijing: Beijing Institute of Technology, 2006. |
| [10] |
胡晓棉. 电爆炸箔起爆系统的设计优化、数值模拟及安全性[D]. 北京: 北京理工大学, 1998.
HU Xiao-mian. Design, numerical simulation, and safety of exploding foil initiation system[D]. Beijing: Beijing Institute of Technology, 1998. |
| [11] |
Frank P I, David P D.
Fundamentals of Heat and Mass Transfer[M]. 4th edition. John Wiley & Sons: New York, 1996, 4th edition. |
| [12] |
Burgess T J. Electrical resistivity model of metals[C]//4th International Conference on Megagauss Magnetic-Field generation and related Topic, Santa Fe, N. Mex, 1986
|
| [13] |
Tsang T.
Classical Electrodynamics[M]. World Scientific: New Jersey, 1999 |
| [14] |
谭迎新, 张景林, 谭汝媚. 飞片起爆试验装置中能源供给系统的性能[J].
火炸药学报, 2005, 28(1): 22-24. TAN Ying-xin, ZHANG Jing-lin, TAN Ru-mei. Properties of the supplying power system for the flyer-initiating device[J]. Chinese Journal of Explosives & Propellants, 2005, 28(1): 22-24. |
| [15] |
Resnick R, Halliday D.
Physics[M]. Wiley International Edition: New York, 1966 |
| [16] |
Dolan T J.
Fusion Research: Principles, Experiments and Technology[M]. Pergamon Press: Oxford, 2000 |
| [17] |
Baginski M E, Baginski T A, Thomas K. A comparison of the electrodynamics of metal under the action of large electric currents[J].
Inter J Applied Electromagnetics and Mechanics, 1996, 7: 193-202. |
| [18] |
Baginski M E, Shaffer E C, Thomas K A. A comparison of the electrodynamics of metal under the action of large electric currents[J].
Inter J Applied Electromagnetics and Mechanics, 2000, 11: 79-93. |
| [19] |
伍俊英, 冯长根, 陈朗. 金属电爆炸等离子体辐射温度测量[J].
战术导弹技术, 2006(5): 31-33. WU Jun-ying, FENG Chang-gen, CHEN Lang. Plasma radiation temperature measurement of metal explosion[J]. Tactical Missile Technology, 2006(5): 31-33. |
| [20] |
Michael J M, Ronald J A. particle response to shockwaves in solids: dynamic witness plate/PIV method for detonations[J].
Experiments in Fluids, 2007, 43(2-3): 163-171. DOI:10.1007/s00348-007-0254-x |
| [21] |
伍俊英, 陈朗, 王飞. 金属桥箔电爆炸等离子体流场实验研究[J].
北京理工大学学报, 2011, 31(1): 1-4. WU Jun-ying, CHEN Lang, WANG Fei. Experimental study of plasma evolution produced by metal bridge foil exploding[J]. Transactions of Beijing Institute of Technology, 2011, 31(1): 1-4. |

The thermal-electrical performance of small-scale copper bridge foils was simulated using finite element method.



