防爆罐是一种用于临时存放、运输爆炸物或可疑爆炸物的罐状装置,可以有效削弱爆炸冲击波和碎片对周围环境的杀伤效应。近些年, 恐怖分子活动猖獗,突发爆炸事件呈上升趋势。为管控恐怖爆炸袭击对社会的危害, 公安部门在车站、机场等公共场所大量使用防爆罐紧急处理可疑爆炸物品。因此, 防爆罐研制具有十分重要的现实意义。目前,防爆罐主要采用厚实的高强特种钢板制造而成,也有使用薄钢板与胶板、树脂、多孔纤维束等有机材料复合制作而成。前者抗爆能力强,但造价昂贵、过于笨重; 后者重量虽然有所降低,但是抗爆特性较差。其共同的缺点是不可重复使用。因此,设计重量轻、抗爆能力强、成本低、可重复使用的防爆罐已经成为公共安全领域的迫切需求。
1960年Baker[1]最先对薄壁球壳的弹塑性响应问题进行理论研究; Dem-chuk[2]利用冲量近似方法推导出了容器壳体的动态应力计算公式,即Baker-Demchuk应力准则; Duffey[3]采用试验方法结合理论分析研究了中心爆炸载荷作用下长圆柱形爆炸容器壳体的弹塑性动力响应; 同时前苏联和美国进行了大量的爆炸容器缩比实验研究。我国爆炸容器的研究起步较晚,直到20世纪80年代末才有相关论文公开发表[4-9]。本研究在此基础上利用非线性动力分析软件ANSYS/LS-DYNA,对内置柱壳/组簧和泡沫铝夹层的新型防爆罐抗爆特性进行数值模拟,对爆炸容器内部超压流场、壳体动力响应以及缓冲吸能机理进行分析,对该防爆罐的抗爆能力和重复使用性进行初步评估,为该类爆炸容器抗爆机理研究和装备研制提供依据。
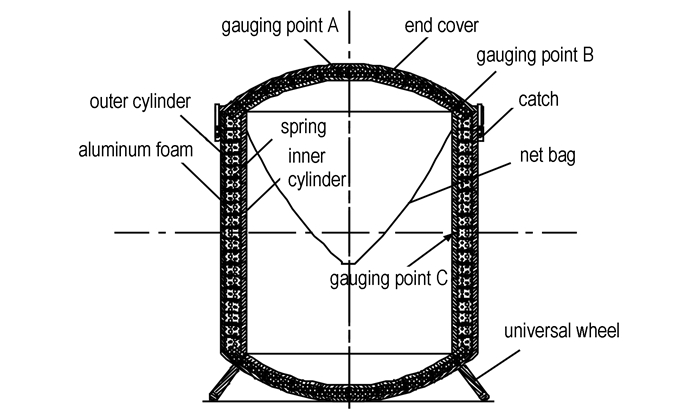
2 计算模型建立设计了一种内置柱壳/组簧和泡沫铝夹层的防爆罐新结构,如图 1所示。其主要特征是罐体采用综合吸能复合结构,即内筒为四个柱壳型薄板叠加环绕构成,柱壳型薄板的重合角度为10°,内外层之间充填泡沫铝,内层每片柱壳型薄板通过轴向中线的一排弹簧组与外层壳体相连。在爆炸载荷的作用下,利用4组轴向均布的组簧弹性变形、充填在内外壳之间的泡沫铝材料塑性变形、4个柱壳型薄板片簧的弹性变形等综合吸收爆炸能量,以及内层柱壳型薄板片簧的抗爆炸破片,实现罐体综合吸能防爆功能。上下端盖采用与筒体相同的吸能原理和抗爆结构。上下端盖与圆筒之间采用扣锁或螺杆紧固连接。该防爆罐在3 kg TNT当量以下可以通过更换泡沫铝夹层实现重复使用。
|
图 1 防爆罐结构示意图 Fig.1 Sketch of anti-explosion container |
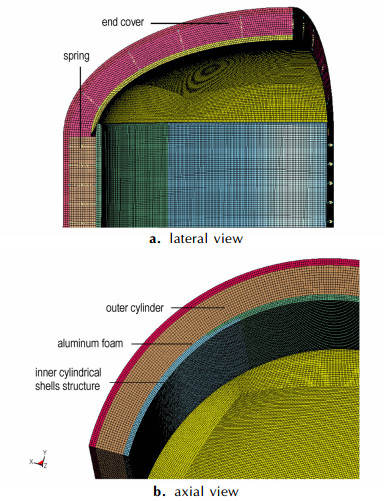
防爆罐内径为100 cm,外径为120 cm,内层钢板厚度为1.4 cm,外层钢板厚度为1.6 cm,泡沫铝夹层厚度为7 cm,防爆罐圆柱部分高度为100 cm,椭球形顶盖部分高度为34 cm。3 kg TNT球形装药在罐体中心爆炸。为了简化计算,将外筒看做一个整体,数值计算模型为1/8模型,采用流-固耦合算法来模拟爆炸冲击波对筒体的作用,模拟结果比解耦算法更具有真实性和准确性。其中炸药和空气均采用ALE算法,编为一个ALE多物质组; 筒体采用Langrange算法; 筒体和ALE多物质组之间应用流-固耦合。钢板和泡沫铝采用自动面面接触,定义动态摩擦系数、粘性阻尼系数(避免接触震荡)。另外软硬材料接触必须选择合适的接触刚度,因此调用基于段(Segment based)的接触算法,可有效避免贯穿。如图 2所示:所有计算网格均采用六面实体单元,空气网格尺寸控制在0.5~0.6 cm,钢板网格尺寸为0.4 ~0.5 cm,泡沫铝网格尺寸为0.6~0.7 cm,计算采用cm-g-μs单位制。流固耦合算法由于其复杂性而不好准确把握,所以前期对流固耦合算法的各项参数进行了调整,解决了钢板不能滑移,以及流体介质渗漏等问题,实现了计算过程的稳定可靠。
|
图 2 三维有限元模型示意图 Fig.2 Sketch of 3D finite element Structure |
采用Mat_High_Explosive_Burn材料模型和JWL状态方程描述炸药材料的物理化学性质。JWL方程p-V关系如下:
| $ {{\rho }_{\rm{eos}}}=A\left[1-\frac{\omega }{{{R}_{1}}V} \right]{{e}^{-{{R}_{1}}V}}+B\left[1-\frac{\omega }{{{R}_{2}}V} \right]{{e}^{-{{R}_{2}}V}}+\frac{\omega {{E}_{0}}}{V} $ | (1) |
式中, peos为爆轰产物压力,GPa; A、B、R1、R2、ω为试验确定的常数; V为相对体积, E0为单位体积的初始内能。具体参数见表 1。
| 表 1 TNT炸药参数[10] Tab.1 Parameters of TNT explosive |
内外筒壁及端盖均为35CrMnSi合金钢板材,数值计算采用Plastic-Kinematic模型,随动硬化系数β=1。该模型考虑了材料的弹塑性特性、强化效应以及应变率效应,其方程为:
| $ {\sigma _y} = \left[{1 + {{\left( {\frac{{\bar \varepsilon }}{C}} \right)}^{\frac{1}{P}}}} \right]\left( {{\sigma _{\rm{s}}} + \beta {E_{\rm{p}}}\varepsilon _{\rm{p}}^{{\rm{eff}}}} \right) $ | (2) |
式中, σy为应变率效应和随动硬化效应下的屈服强度,GPa; ε为加载应变率, 爆炸加载的应变率通常在104 s-1以上; C、P为材料应变率相关常数; εpeff为有效塑性应变; β为随动硬化系数; σs为材料的初始屈服强度, GPa; Ep为塑形硬化模量, GPa; E为弹性模量, GPa。具体材料参数见表 2,其中fs为失效应变。由于计算中35CrMnSi合金钢的最大塑性应变在0.2%以下,没有出现较大塑性变形,且35CrMnSi在爆炸加载下的高应变率相关参数需要试验获得,因此可暂不考虑应变率效应,取C、P均为零。
| 表 2 防爆罐罐体的材料参数[11] Tab.2 Parameters of material used by anti-explosion container body |
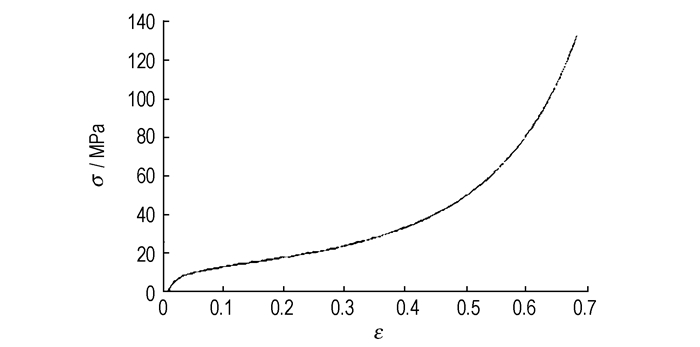
泡沫铝材料采用*MAT_CRUSHABLE_FOAM本构模型,本构关系需要输入材料的应力应变曲线。本研究采用725-PML泡沫铝,其应力应变曲线如图 3所示,其它参数[12]分别为: ρ0=0.33×103 kg·m-3, E=0.25 GPa, 泊松比υ=0.3,pcut=8.6 MPa,阻尼系数为0.1。
|
图 3 泡沫铝应力应变曲线 Fig.3 Stress-strian curve of aluminum foam |
弹簧采用SECTION_DISCRETE离散单元,用线弹性弹簧模型*MAT_SPRING_ELASTIC进行模拟。弹簧刚度k=100 N·mm-1,为避免时步长过小,设定离散单元节点的质量为10 g。
3.5 空气材料模型及参数计算模型中空气采用空物质材料本构模型,其密度ρ0=1.29 kg·m-3; 空气的状态方程形式如(3)式:
| $ p = \left( {{C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3}} \right) + \left( {{C_4} + {C_5}\mu + {C_6}{\mu ^2}} \right){E_0} $ | (3) |
式中, p为压力; C1~C6均为常数; μ=1/(V0-1),其中μ为体积应变参数,V0为初始相对体积; E0为单位体积的初始能量。具体参数见表 3。
| 表 3 空气状态方程参数[10] Tab.3 Parameters of air |
在大量理论和试验研究的基础上,前人总结了一些球形装药空气中爆炸冲击波超压半经验半理论计算公式。其中亨利奇公式[13]被广泛应用,表示为:
| $ \left. \begin{array}{l} \Delta {p_m} = \frac{{1.40717}}{{\bar r}} + \frac{{0.55397}}{{{{\bar r}^2}}}-\frac{{0.03572}}{{{{\bar r}^3}}} + \frac{{0.000625}}{{{{\bar r}^4}}}\left( {0.05 \le \bar r \le 0.3} \right)\\ \Delta {p_m} = \frac{{0.61938}}{{\bar r}} + \frac{{0.03262}}{{{{\bar r}^2}}} + \frac{{0.21324}}{{{{\bar r}^3}}}\left( {0.3 \le \bar r \le 1} \right) \end{array} \right\} $ | (4) |
式中, r为比例距离,单位为m·kg-1/3; Δpm为测点r处的冲击波峰值超压,单位为MPa。
林俊德[14]给出了0.2~3 m·kg-1/3比例距离范围内,爆炸容器壁面冲击波入射超压和反射超压峰值计算公式:
| $ \Delta {p_1} = 0.75\bar r-2.06, \;\;\;\;\;\Delta {p_2} = 4.5\bar r-2.6 $ | (5) |
上述经验方法简单方便,在实际工程计算中获得了较多的应用。
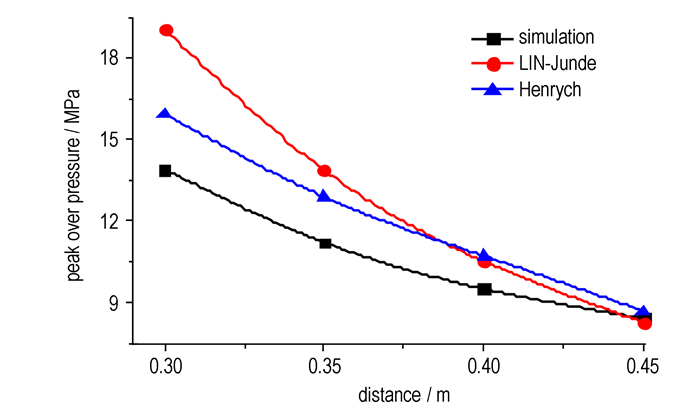
本研究采用质量为3 kg、直径为0.152 m的TNT球形装药,计算得到距防爆罐中心水平距离分别为0.3,0.35,0.4,0.45,0.5 m处的冲击波峰值超压,并与公式(4)和公式(5)理论计算结果进行对比,结果见表 4。
| 表 4 不同距离冲击波峰值超压计算值与理论值对比 Tab.4 Comparison of the calculated values with theoretical ones of shock wave peak value overpressure in different distances |
图 4给出了数值计算与经验公式的对比曲线:当r < 0.35 m,仿真计算值与理论值的相对误差较大。这是因为小于0.35 m对应的比例距离处于公式(4)和公式(5)适用范围的边界,公式计算结果的误差相对较大。随着比例距离的增加,误差逐渐减小,当r=0.4,0.45 m,相对误差在10%以内。因此,参考以上两种理论计算结果,可以认为本模型对防爆罐爆炸流场的模拟结果是可信的。
|
图 4 用数值计算与经验公式得到的Δpm-r关系曲线 Fig.4 Curves of Δpm-r obtained by numerical calculation and empirical formulas |
密闭容器内球形装药爆炸作用过程的仿真结果如图 5所示。首先是爆炸空气冲击波在防爆罐内的形成,如图 5a所示。当t=125 μs时,空气冲击波在防爆罐侧壁中环发生规则反射,如图 5b所示。然后球面爆炸冲击波与防爆罐圆筒壁发生斜反射,随着轴向距离的增大,斜反射角逐渐增大,当入射角大于规则斜反射临界角φ,规则斜反射转变为马赫反射。根据C.N.Kingery和B.F.Panill试验得到的入射波规则斜反射临界角φ与入射峰值超压Δp1的关系[13]可知:当入射超压Δp1为5~10 MPa,规则反射临界角介于41°~43°。对于本研究防爆罐内筒长径比为1:1,因此在波阵面即将到达筒身端盖结合部时,开始发生马赫反射,由于马赫反射波强度远大于入射波,马赫杆传播速度增大,开始追赶入射波。当t=250 μs时,空气冲击波到达端盖弧面,如图 5c所示,此后马赫反射波从端盖底部沿着端盖壁面向端盖中心位置汇聚,如图 5d所示。当t=475 μs时,反射波在端盖中心完成汇聚,压力骤然升高,达到170.6 MPa,是圆筒中环面正反射超压的两倍左右,如图 5e所示。当t=625 μs时,冲击波经过两个端盖面反射作用后再次在防爆罐中心汇聚,如图 5f所示。汇聚压力波将对防爆罐开始新的冲击作用过程,但之后的压力波阵面不再清晰,反射情况更为复杂,压力也急剧下降,而这样的脉动作用过程要持续多次。表 5是防爆罐典型位置冲击压力脉动峰值的仿真计算结果。其中A为内端盖顶部中心位置,B为筒身端盖结合位置,C为中环面位置。具体位置如图 1所示。
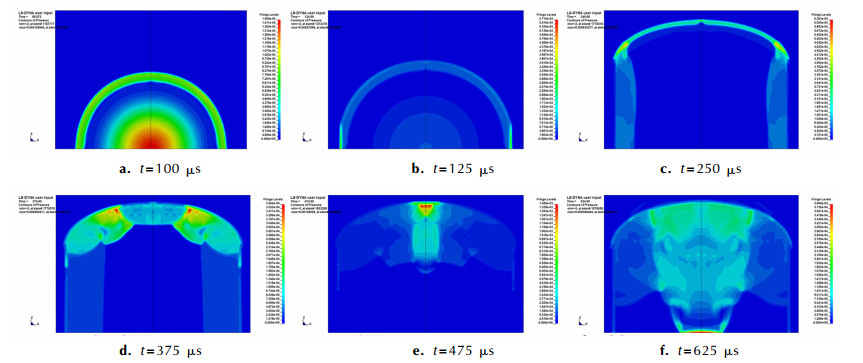
|
图 5 爆炸冲击波与防爆罐筒壁作用过程 Fig.5 The process of blast wave act on anti-explosion container wall |
| 表 5 典型位置压力脉动峰值 Tab.5 Peak value of pressure fluctuation in typical positions |
图 6为上文所述典型位置的单位面积冲量——比冲量[13]的时程变化曲线。由图 6可以看出,由于爆炸冲击波在防爆罐内壁的多次反射、汇聚和再次反射,使内壁承受的比冲量经历数次阶跃上升过程,以顶盖中心位置出现的阶跃现象最为显著,冲击作用比冲量水平也最高。表明:上下端盖中心部位是该型防爆罐强度设计关注的重点。
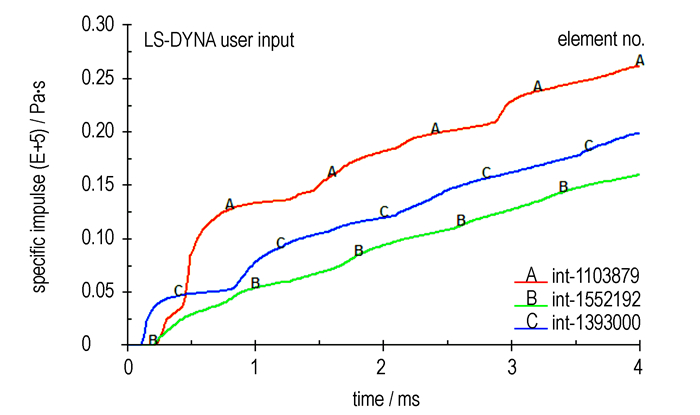
|
图 6 典型位置比冲量时程变化曲线 Fig.6 Time history curves of specific impulse in typical positions |
仿真计算结果的应力应变分析表明:爆炸作用过程中防爆罐圆柱部分内壳并没有发生塑性变形,由于边界效应,最大等效大应力出现在板壳上沿、约为799 MPa,与装药中心等高的柱壳中环位置最大等效应力约为633 MPa,均小于板壳材料的屈服强度。上下端盖椭球形内壳中心区域是防爆罐承受爆炸冲击荷载最危险的部位,爆炸作用下产生的最大等效应力仍小于壳体材料的弹性极限,约为1000 MPa,也不会产生塑性变形。因此,依据数值计算结果,本文研究的防爆罐结构在3 kg炸药中心爆炸条件下不会破坏,可以满足可重复使用要求。
4.3 防爆罐复合吸能机理与效应研究图 7是防爆罐圆筒部分的圆柱形薄板壳、组簧和泡沫铝运动与变形吸能过程仿真结果。由图可以看出:内筒四片柱壳型薄板在爆炸冲击波作用下,压缩轴向组簧的同时挤压泡沫铝作向外的径向变形运动,柱壳型薄板之间发生相对滑移,当t=3 ms时刻泡沫铝夹层已经被压实,相对滑移终止。同时由图 8可看出:柱壳型薄板端部圆角沿内端盖的切边滑移,t=1 ms时刻两者脱离接触,这种设计保证了最大限度的密闭性。综上所述:四片柱壳型薄板以及罩在两端的内端盖向“前后左右上下”6个方向展开,同时内筒将冲击波的能量通过应力波的形式传递给泡沫铝夹层。泡沫铝夹层发生塑性变形,吸收爆炸冲击能量,从而降低内筒承受的爆炸压力,提高了内筒的抗爆炸冲击能力。经过泡沫铝夹层的缓冲吸能作用,使外筒一直保持弹性形变状态。

|
图 7 缓冲吸能历程轴向视图 Fig.7 Axial view of cushion and energy-absorbing course |

|
图 8 缓冲吸能历程侧向示图 Fig.8 Lateral view of cushion and energy-absorbing course |
同时总共有100个弹簧参与缓冲吸能,这些弹簧既可以将内外筒连接成一个整体,也可以保证爆炸后内筒恢复到初始位置。在整个过程中,四片柱壳型薄板都控制在弹性形变之内。t=3 ms以后缓冲吸能过程结束,筒壁出现周期性的振动响应,筒内压力逐渐转变为准静态压力。
4.4 缓冲吸能特性分析爆炸冲击能量主要以应力波的形式传入泡沫铝夹层,然后以弹塑性波的形式传播[15]。其能量被泡沫铝孔的塑变、失稳、坍塌、破裂以及胞壁摩擦等形式耗散和吸收,产生良好的缓冲吸能效果。
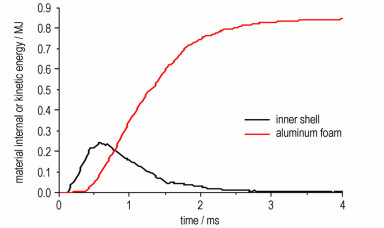
由于计算时采用理想气体状态方程,所算出的冲击波超压明显低于所有经验公式的理论值。而实际高温高压气体的状态不同于理想气体,如果考虑诸如空气分子的离解和电离这样的实际气体效应的话,冲击波超压值应该大很多[13]。尤其是对于内爆炸超近场作用的数值计算,这种效应更加明显,目前还没有可靠地计算模型将这个因素考虑在内。因此参照各经验公式,将炸药状态参数中的E0调整为0.0101 MJ,则3 kg TNT爆炸释放的总能量为18.5 MJ,由图 9可知:泡沫铝吸收的能量为0.88 MJ,加上弹簧吸收的0.005 MJ能量,泡沫铝和弹簧吸收的总能量为大约为炸药总能量的4.8%。而钢板由于没有发生塑性形变,弹性形变吸收的总能量仅为0.0112 MJ,不到炸药总能量的0.1%。这是由于大部分能量都转化为爆炸产物气体和空气的内能。由图 10可知:炸药和空气组成的ALE多物质组的初始能量为18.6 MJ,其中炸药的能量为18.5 MJ,另外0.1 MJ为空气初始能量,炸药的能量在90 μs的时间内迅速释放,由于时间极短,空气可认为是绝热压缩。71%的能量转化为爆轰产物和空气介质的动能,形成爆轰波和空气冲击波,爆炸产物气体和空气的内能急速下降到5.4 MJ的低谷,这些内能大部分储存在爆轰产物中; 当冲击波受到容器壁面的阻滞,其动能一部分传递给钢板,一部分转化为自身的内能,形成高温高压气体,欧拉场的内能在400 μs内再次达到16.95 MJ的峰值,其吸收的能量占炸药总能量的87%。在密闭空间这种内能的耗散过程要缓慢得多,当t=4 ms时,仍有64%炸药总能量存在于爆炸产物气体和空气的内能里。
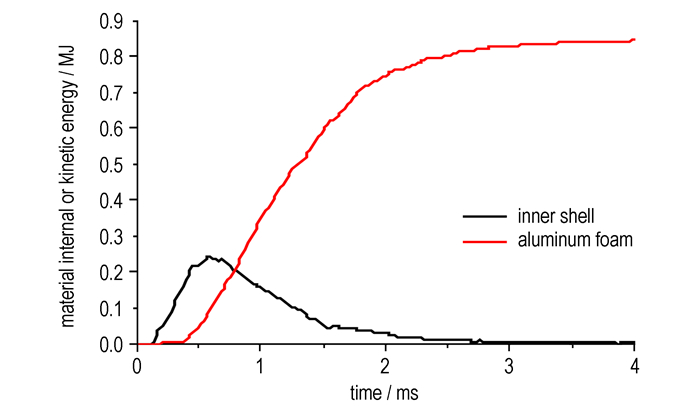
|
图 9 内筒钢板动能和泡沫铝内能时程曲线 Fig.9 Time history curves of internal energy for aluminum foam and internal cylinder steel plate |
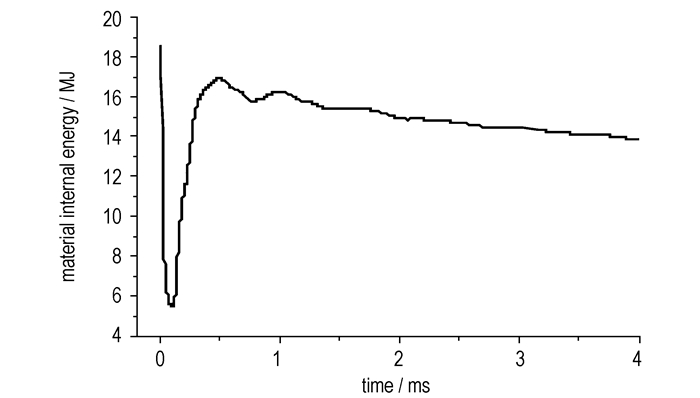
|
图 10 爆炸产物气体和空气内能时程曲线 Fig.10 Time history curves of internal energy in explosion products and the air |
如图 9所示:爆炸初始阶段内筒钢板获得的最大动能为0.24 MJ,根据能量守恒,这些动能如果全部转化为重力势能,足以将100 kg的钢铁抛掷到24 m的高空,如果内筒是完整封闭的,这些能量肯定都要转化为塑性变形能。而开放式内筒几乎将这些能量全部传递给了泡沫铝夹层。泡沫铝吸收的能量之所以远高于内筒钢板的最大动能,是因为还有0.64MJ的能量是通过应力波的形式传入泡沫铝夹层的。如图 11所示:应力波在泡沫铝介质中维持了2 ms高应力平台、高量能消耗的弹塑性传播,泡沫铝夹层的最大压缩量达到64%,其应力平台达到10~13 MPa。可见泡沫铝夹层可以通过卸载动能和透射应力波的形式很好地转移、吸收内层钢板所获得的冲击能量。
|
图 11 泡沫铝夹层压缩方向应力曲线 Fig.11 Stress curves of aluminum foam in the compression direction |
利用非线性动力学程序LS-DYNA对柱壳组簧内置泡沫铝夹层的防爆罐在3 kg TNT爆炸载荷作用下的抗爆特性进行数值模拟。结果表明:
(1) 数值模拟能够较好地反映容器内部爆炸载荷的分布规律和衰减规律,得到了试验过程中无法捕捉的信息,容器壁面压力载荷呈现多次脉动特征,比冲量载荷经历数次阶跃上升。这是爆炸容器结构破坏的重要因素。
(2) 柱壳/组簧结构可以在高强度的爆炸冲击载荷作用下不产生塑性形变,同时将能量更加均匀地传递给泡沫铝夹层,防爆罐的抗爆能力显著提高。对于椭球封顶的防爆罐,端盖中心位置的是危险区域,最容易产生塑性变形。
(3) 对防爆罐内部爆炸产物、空气与各结构间的能量转化与吸收进行了定量分析,泡沫铝夹层可以通过卸载动能和透射应力波的形式很好地转移、吸收内层钢板所获得的冲击能量。起到很好的缓冲效果。
| [1] |
Baker W E. The elastic-plastic response of thin spherical shells to internal blast loading[J].
Journal of Applied Mechanics, 1960, 27: 139-144. DOI:10.1115/1.3643888 |
| [2] |
Demehuk A F. A calculation method for explosive chamber[J].
Joumal of Applied Mechanics and Technical Physics, 1968, 5: 47-50. |
| [3] |
Ko W L, Pennick H G, Baker W E. Elastc-plastic response of a multi-layered spherical vessel to internal blast loading[J].
International Journal of Solids and Structures, 1977, 33(6): 503-514. |
| [4] |
赵士达. 爆炸容器[J].
爆炸与冲击, 1989, 9(1): 85-97. ZHAO Shi-da. Blast chamber[J]. Explosion and Shock Waves, 1989, 9(1): 85-97. |
| [5] |
段卓平. 密闭爆炸容器实验研究及数值模拟[J].
中国安全科学学报, 1994, 4(3): 1-7. DUAN Zhuo-ping. The experimental study and numerical simulation of explosion chamber[J]. China Safety Science Journal, 1994, 4(3): 1-7. |
| [6] |
霍宏发, 于琴, 黄协清. 组合式爆炸容器冲击载荷及其动力响应的数值模拟[J].
西南交通大学学报, 2003, 38(5): 513-516. HUO Hong-fa, YU Qin, HUANG Xie-qing. Numerical simulation of dynamical responses of assembled vessel to explosion impact load[J]. Journal of Southwest Jiao tong University, 2003, 38(5): 513-516. |
| [7] |
饶国宁, 陈网桦, 王立峰, 等. 内部爆炸载荷作用下容器动力响应的数值模拟[J].
中国安全科学学报, 2007, 17(2): 129-133. RAO Guo-ning, CHEN Wang-hua, WANG Li-feng, et al. Numerical simulation of dynamic response of vessels subjected to internal load of blast[J]. China Safety Science Journal, 2007, 17(2): 129-133. |
| [8] |
张亚军, 徐胜利. 中心内爆引起的圆柱壳流固耦合问题的数值模拟[J].
中国科学技术大学学报, 2007, 37(1): 6-12. ZHANG Ya-jun, XU Sheng-li. Numerical simulation on flow structure interaction loaded by a blast wave from a central charge[J]. Journal of University of Science and Technology China, 2007, 37(1): 6-12. |
| [9] |
宋延泽, 田锦邦, 赵隆茂, 等. 离散多层绕带容器在爆炸载荷作用下动力响应的数值模拟研究[J].
爆炸与冲击, 2008, 28(4): 324-330. SONG Yan-ze, TIAN Jin-bang, ZHAO Long-mao, et al. Dynamic responses of discrete muhilay-ered wound ribbon vessels subjected to blast loading[J]. Explosion and Shock Waves, 2008, 28(4): 324-330. DOI:10.11883/1001-1455(2008)04-0324-07 |
| [10] |
李裕春, 时党勇, 赵远.
ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008: 235-296.
|
| [11] |
张祖贤, 邢安定, 汪喜, 等.
兵器黑色金属材料手册[M]. 北京: 兵器工业出版社, 1990.
|
| [12] |
王永刚, 胡时胜, 王礼立. 爆炸荷载下泡沫铝材料中冲击波衰减特性的实验和数值模拟研究[J].
爆炸与冲击, 2003, 23(6): 516-522. WANG Yong-gang, HU Shi-sheng, WANG Li-li. Shock attenuation in aluminum foams under explosion loading[J]. Explosion and Shock Waves, 2003, 23(6): 516-522. |
| [13] |
叶序双.
爆炸作用基础[M]. 南京: 工程兵工程学院, 2004.
|
| [14] |
霍宏发. 组合式爆炸容器动态特性分析及实验研究[D]. 西安: 西安交通大学, 2000.
http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y350433 |
| [15] |
王礼立.
应力波基础[M]. 北京: 国防下业出版社, 1985.
|
The blast resistant characteristics of anti-explosion container built-in cylindrical shells/group spring and aluminum foam sandwich under 3 kg TNT explosion impact loading were numerically simulated using LS-DYNA explicit non-linear dynamic finite element analysis (FEA) program. The energy conversion and absorption between all parts in anti-explosion container were analyzed.




