固体推进剂燃烧可以快速产生大量的高温气体,在军事(火箭、导弹)和民用(安全气囊燃气发生器)方面都得到了广泛的应用[1-3]。固体推进剂的点火是通过化学反应达到能自身维持稳定燃烧的初期阶段[4]。激光点火能量流从光源到试样不但可进行高精度测量与控制重现,而且能够满足宽区间的热流实验要求[5]。激光-固体推进剂点火行为的研究工作主要包括:点火模型、点火延迟、点火温度、点火判据、作用机理等[6-9]。点火模型大致可分为三类:固相反应模型、气相反应模型与异相反应模型[10]。固相反应模型假设稠密相中的化学反应放热过程占主导地位,忽略了表面与气相反应过程; 并假设激光辐射能体吸收服从Bouguer定律且化学反应速率服从Ahrrenius定律[11],点火判定依据其表面温度的快速上升或出现发光现象,该模型通过实验与数值计算的验证,可广泛应用。
与固相点火模型不同的是,本研究深入分析以激光为点火源的固相反应模型点火机理,将点火过程分为吸热热解、边界层气相掺混与快速化学反应三个阶段考虑,结合点火判据的边界条件,建立一种预测固体推进剂激光点火特性参数的阶段点火模型,并与文献及固相点火模型计算结果进行对比。
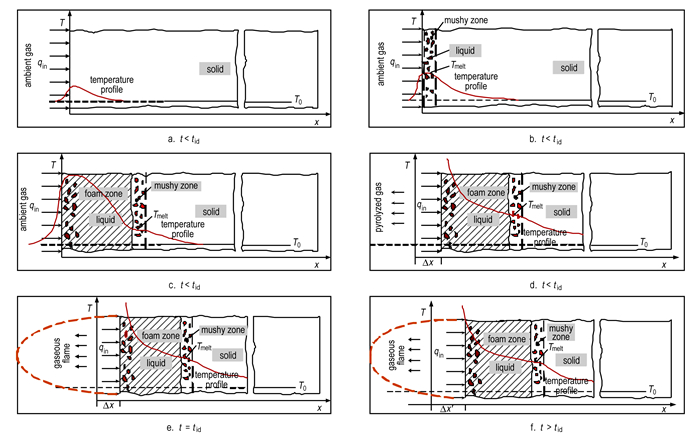
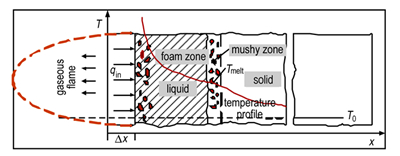
2 激光点火机理固相反应模型点火机理主要分为两个阶段:固体推进剂内部绝热爆炸引起的惰性诱导期与化学反应引起的温度快速上升期[12]。前者主要在给定的边界条件下求解绝热平衡方程; 后者主要考虑当前期热解过程达到一定程度,引起内部剧烈的化学反应致使近表面局部温度快速上升并产生火光现象。Liau[13]对黑索今(RDX)单元推进剂激光点火的热物理-化学过程描述如图 1所示。tid为点火延迟时间,T0为固体推进剂初始温度。首先,当激光开始作用到RDX单元推进剂表面时,推进剂吸收激光能量并开始热分解,表面温度上升(图 1a)。其次,当表面温度达到推进剂熔点,而又不能瞬间吸收足够的能量使其全部熔化,温度无法继续升高,形成了固-液两相区(图 1b)。接着,当液相完全形成,在热传导与辐射换热作用下,固-液交界面开始向推进剂内部移动(图 1c)。随后,在液相区由于热分解和经历一系列的化学反应,发生相变形成局部气-液两相区,并在表面快速气化(图 1d)。继而,当热流足以激励自身加速化学反应的进行,致使气相释放大量的热并产生发光现象,此时点火发生(图 1e)。最后达到稳定燃烧状态(图 1f)。
|
图 1 RDX单元推进剂激光点火热物理-化学过程[13] Fig.1 Thermophysical and chemical process of laser induced ignition of RDX monopropellant |
推进剂激光固相点火模型主要基于固相热传导,热平衡方程与边界条件如式(1) [14]所示。
| $ \left\{ \begin{array}{l} pc\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {x^2}}} + \rho QA{{\rm{e}}^{-E/RT}} + \left( {1-f} \right)\beta {I_0}{{\rm{e}}^{-\beta x}}\\ T\left( {x, 0} \right) = {T_0};\;\;\partial T/\partial t\left( {0, t} \right) = 0;T\left( {\infty, t} \right) = {T_0} \end{array} \right. $ | (1) |
式中,ρ为密度,kg·m-3; c为比热容,J·kg-1·K-1; T为温度,K; t为时间,s; x为坐标,m; λ为导热系数,W·m-1·K-1; Q为化学反应热, J·kg-1; A为指前因子, s-1; E为活化能,J·mol-1; R为气体常数,J·mol-1·K-1; f为反射率; β为衰减系数,m-1; I0为有效激光的强度, I0=(1-f)Iir,W·m-2; Iir为入射激光强度; T0为初始温度,K。
点火判据主要分为两类:临界温度与临界热流。Strakovskiy[15]结合Vilyunov [4]和Merzhanov[16]的热平衡假设,提出以单位表面积化学反应热释放率为点火判据,依据此判据在计算化学反应阶段的点火温度与点火延迟时间的误差分别约为2%与3%。
| $ {Q_ + } = B{I_0} $ |
式中,Q+为单位表面积化学反应热释放率, W·m-2; Q+(x*)=Qρzx*exp(-E/RTi),z为化学反应时间因子,s; x*为化学反应宽度; B为输入激光强度因子,受活化能E的影响。
B=4.1[β(atid)1/2]1/4[E(Ti-T0)/RTi2]
式中,a为热扩散系数,a=λ/ρc,m2·s-1; tid为点火延迟时间,s; Ti为点火温度,K。
3.2 分阶段点火参数计算方法激光对固体推进剂的点火过程,主要受热解过程、化学反应、临界温度、固体推进剂的光学参数(衰减率与吸收系数)、激光强度等的影响。为此,从固体材料强制点火角度出发, 可将其点火过程分为三个阶段:吸热热解、边界层气相掺混与快速化学反应[17]。从而,点火延迟时间tid可表示为:
| $ {t_{{\rm{id}}}} = {t_1} + {t_2} + {t_3} $ | (4) |
式中,t1为激光开始作用到包含气体燃料的热解产物所需临界温度Tpy的时间,s; Tpy为推进剂熔点,K; t2为可燃燃料浓度扩散输运时间,s; t3为可燃混合物化学反应直至点火燃烧的时间,s。
3.2.1 热分解阶段由固体推进剂表面有效热流I0及能量守恒定律,则:
| $ {I_0} = {\left. {-\lambda \left( {\partial T/\partial x} \right)} \right|_{x = 0}} $ | (5) |
鉴于热解区域仅发生在表面很薄一层内,故在临界温度Tpy时刻:
| $ {\left. {-\lambda \left( {\partial T/\partial x} \right)} \right|_{x = 0}} \approx \lambda \left( {{T_{{\rm{py}}}}-{T_\infty }} \right)/\sqrt {a{t_1}} $ | (6) |
从而有:
| $ {t_1} \approx \lambda \rho c{\left[{\left( {{T_{{\rm{py}}}}-{T_\infty }} \right)/{I_0}} \right]^2} $ | (7) |
对于热解产物与空气掺混过程时间t2,由平板热对流及边界条件:
| $ hl/\lambda = 0.21{\left( {Gr\mathit{Pr}} \right)^{2/5}} $ | (8) |
式中,Gr为格拉晓夫数; Gr=g[(Ts-T∞)/T∞](l3/ν2),Ts为推进剂沸点温度,K; Pr为普朗特数,Pr=ν/a,l为特征长度,m; ν为运动粘度,m2·s-1。同时,对流换热系数(h)有:
| $ h \approx {\lambda _{\rm{g}}}/\delta \approx {\lambda _{\rm{g}}}/\sqrt {{a_{\rm{g}}}{t_2}} $ | (9) |
式中,λg为混合气体导热系数,W·m-1·K-1; ag为混合气体热扩散系数,m2·s-1。从而有:
| $ {t_2} \approx 2.267 \times {10^3}{l^2}/{\left[{{a_{\rm{g}}}\left( {Gr \cdot \mathit{Pr}} \right)} \right]^{4/5}} $ | (10) |
对于点火温度Ti,化学反应直至点火的时间t3=0.21ro2/ag,ro为试样特征尺度,m。临界Damkohler数δc=(E/RT∞)ro2Qzexp(-E/RT∞)/kT∞,对于平面热源,δc=0.88,从而有:
| $ {t_3} = 0.1848\left( {RT_{\rm{i}}^2/E} \right)\left( {c/Qz} \right){\rm{exp}}\left( {E/R{T_{\rm{i}}}} \right) $ | (11) |
不难发现,式(3)与式(11)分别从固相与气相反应角度描述化学反应时间,但总的来讲,化学反应时间占总体点火时间是很小的,故可以忽略不计。但鉴于点火温度受激光能量的影响,式(3)更能全面反应内在联系,但T0应为熔点温度。
3.3 数值计算以HMX单元推进剂激光点火为例[12],当初温T0=293 K时,激光入射强度分别为:45, 76, 170 W·cm-2,实验测得点火延迟时间206, 99, 36 ms,采用固相点火模型式(1)计算点火温度分别为:550, 565, 595 K,反求化学动力学参数:Q=2360 J·g-1, E=177.9 kJ·mol-1和z=1.04E15 s。计算参数:密度ρ=1740 kg·m-3,比热c=1460 J·kg-1·K-1,热扩散率a=0.99×10-5 m·s-1,导热系数λ=0.2515 W·m-1·K-1,衰减系数β=6/m,化学反应宽度x*=50 μm,反射率f=0.98。采用式(4), (7), (10)和(11)计算T0=343 K时的点火特性参数如表 1所示。三种激光入射强度下,阶段性点火模型计算的点火延迟时间tia与文献[12]中固相点火模型计算值(tis)和文献[12]实验值(tie)的偏差分别为3.8%,8.1%,11.5%和5.6%,5.4%,19.2%;两种模型计算的点火温度(Tia, Tis)偏差为1.23%,0.87%,0.98%。由此可见,阶段性点火模型计算与文献值及固相点火模型计算一致性较好。
| 表 1 阶段性点火模型计算的HMX推进剂激光点火特性参数与文献值对比 Tab.1 Characteristic parameters of laser ignition for HMX propellant from phase-ignition model and reference |
通过深入分析激光对固体推进剂的作用机理和强化点火理论,将其点火过程分为热解、对流换热与强烈化学反应三个阶段,从而建立了一种固体推进剂激光阶段性点火模型。该模型中点火延迟时间可表示为三个阶段作用时间之和,而点火温度可基于“热平衡假设”的点火判据求得。该阶段性点火模型反映了激光点火过程固体推进剂的化学变化过程,物理意义明确。以某HMX推进剂的激光点火过程为例进行了数值计算,45, 76, 170 W·cm-2三种激光入射强度下,阶段性点火模型计算的点火延迟时间与固相点火模型和文献值的偏差分别为3.8%,8.1%,11.5%和5.6%,5.4%,19.2%;两种模型计算的点火温度偏差为1.23%,0.87%,0.98%。由此可见,阶段性点火模型计算与文献实验值及文献中固相点火模型计算一致性较好。
| [1] |
Michael A W, Quinn B, Tang K C. Solid rocket motor internal ballistics simulation using three-dimensional grain burnback[J].
Journal of Propulsion and Power, 2007, 23(3): 575-584. DOI:10.2514/1.22971 |
| [2] |
董师颜, 张兆良.
固体火箭发动机原理[M]. 北京: 北京理工大学出版社, 1996.
|
| [3] |
Ul as, Kuo K K. Laser-induced ignition of solid propellants for gas generators[J].
Fuel, 2008, 87: 639-646. DOI:10.1016/j.fuel.2007.05.030 |
| [4] |
Vilyunov, V N, Zarko, V E.
Ignition of solids[M]. New York: Elsevier Science Publishers, 1989.
|
| [5] |
Mikheev V F. Propellants Ignition by Light Radiation[C]//Dissertation, Institute of Chemical Kinetics and Combustion, 1970.
|
| [6] |
Strakovskiy L G. Source Mechanism of the ignition of some secondary explosives by a monocharomatic light pulse[J].
Fizika Goreniyai Vzryva, 1985, 21(1): 41-45. |
| [7] |
徐娇, 吴立志, 沈瑞琪, 等. 边界条件对激光性能的影响[J].
中国激光, 2010, 37(2): 418-423. XU Jiao, WU Li-zhi, SHEN Rui-qi, et al. Effect of confinement on the capability of laser ignition[J]. Chinese Journal of Lasers, 2010, 37(2): 418-423. |
| [8] |
郝海霞, 南宝江, 安亭, 等. 含CL-20改性双基推进剂激光点火特性[J].
中国激光, 2011, 38(5): 0502009-1. HAO Hai-xia, NAN Bao-jiang, AN Ting, et al. Laser ignition characteristics of CL-20 composite modified double-Base propellants[J]. Chinese Journal of Lasers, 2011, 38(5): 0502009-1. |
| [9] |
赵兴海, 高杨, 程永生. 激光点火技术综述[J].
激光技术, 2007, 31(3): 306-313. ZHAO Xing-hai, GAO Yang, CHENG Yong-sheng. A summary of laser ignition technology[J]. Laser Technology, 2007, 31(3): 306-313. |
| [10] |
朱荣贵.
固体推进剂燃烧基础[M]. 北京: 中国宇航出版社, 1994.
|
| [11] |
项仕标.
激光点火理论与实践[M]. 郑州: 黄河水利出版社, 2004.
XIANG Shi-biao. Theory and practice of laser ignition[M]. Zhengzhou: Yellow River Water Conservancy Press, 2004. |
| [12] |
Strakovskiy L, Cohen A, et al. Laser ignition of propellants and explosives[R]. AD19980702-136.
|
| [13] |
Liau Y C, Kim E S, Yang V. A comprehensive analysis of laser-induced ignition of RDX monopropellant[J].
Combustion and Flame, 2001, 126(3): 1680-1698. DOI:10.1016/S0010-2180(01)00281-4 |
| [14] |
张领科, 赵威, 吴立志. AP/HTPB复合底排推进剂激光点火燃烧特性[J].
中国激光, 2013, 40(8): 0803005-1. ZHANG Ling-ke, ZHAO Wei, WU Li-zhi. Ignition and combustion characteristics of AP/HTPB composite propellant by laser[J]. Chinese Journal of Lasers, 2013, 40(8): 0803005-1. |
| [15] |
Strakovskiy L G, Ulyakov P I, Frolov E I. Ignition of some high explosives by a laser radiation[C]//Proceeding of the Fifth All-Union Symposium on Combustion and Explosion. Chernogolovka, Russia, 1977.
|
| [16] |
Merzhanov A G, Averson A E. The present state of the thermal ignition theory[J].
Combustion and Flame, 1971, 16(1): 89-124. DOI:10.1016/S0010-2180(71)80015-9 |
| [17] |
Quintiere J G.
Fundamentals of fire phenomena[M]. Chichester John Wiley & Sons Ltd, 2006.
|
The laser ignition process for solid propellant was divided into three steps, thermal decomposition, boundary layer gas mixing and rapid chemical reaction by deep analysis on the mechanics of laser ignition for solid phase reaction model. The prediction model for ignition delay time and ignition temperature of laser ignition was built.



