高能炸药常常由大量炸药晶体、少量粘结剂等添加剂经一定工艺成型,一般拉伸强度小于10MPa、延伸率小于2%[1-2],呈现出低强度脆性断裂特点,不利于武器结构可靠性和安全性。随着先进武器实战化要求提高,对炸药材料增韧改性也是提高武器性能的重要途径[3],但炸药材料韧性不同于强度、弹性模量、延伸率等其他力学性能参量,目前还没有一个非常明确的表征方法。
在工程材料中普遍被接受的韧性表征参量是冲击韧性Ak[4],它是采用落锤或摆锤冲击加载方式测试的,而炸药材料在冲击载荷作用下存在爆炸风险而不能测试其Ak。除冲击韧性Ak外,也有采用断裂韧性KⅠC来表征材料韧性的[4-5],但该测试方法只适合于塑性变形较小的脆性材料,当炸药材料塑性或韧性增加到一定程度时,测试曲线往往不能满足其中“最大载荷”与“条件载荷”之比小于1.10等相关要求[5],此时就不能采用KⅠC进行表征,另外,KⅠC测试方法比较复杂,对于炸药材料的配方及成型技术研究而言,测试繁琐而周期较长。
应力-应变(σ-ε)曲线是材料最为基本的力学性能测试曲线,但一般基于σ-ε曲线进行计算的是强度、模量、延伸率及本构关系等,本研究提出了基于σ-ε曲线的断裂能量计算的韧性表征参量—断裂能,分析比较了断裂能与冲击韧性、断裂韧性的物理意义,同时试验比较了室温下三种炸药(HMX-P1、HMX-P2、TATB-P3)之间以及其中一种炸药(HMX-P2)在不同温度下(20,35,45,60 ℃)的断裂能与断裂韧性变化趋势的异同。
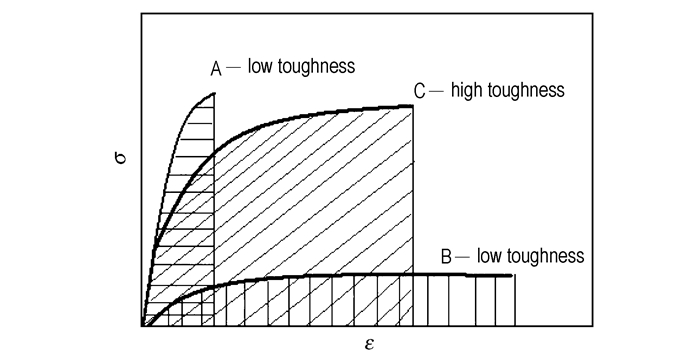
2 断裂能的计算方法材料的韧性目前只有定性的定义:一般表示材料在断裂前吸收能量和进行塑性变形的能力,与脆性相反。韧性好的材料要求既要具有高的破坏强度,同时也要有高的破坏应变,其σ-ε曲线见如图 1中的C曲线,如果只有高的破坏强度(A曲线)、或只有高的破坏应变(B曲线)等均不属于韧性好的材料。从该定性描述中可以看出,韧性较好材料的σ-ε曲线的包络面积相对较大,该包络面积对应的是材料单位体积上吸收的能量。
|
图 1 表示材料韧性高低的σ-ε曲线示意图 Fig.1 σ-ε curves of materials with high or low toughness |
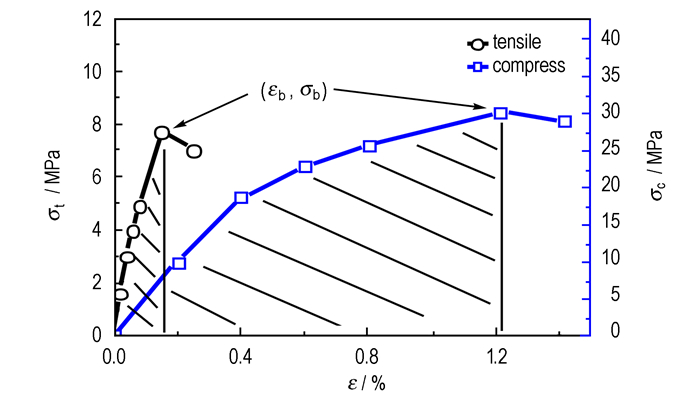
图 2是一种HMX基炸药的拉伸、压缩σ-ε曲线。从图 2可知,炸药压缩破坏强度、压缩破坏应变显著大于拉伸破坏应变与拉伸破坏强度,这也是脆性材料的显著特征之一。从图 2可看出σ-ε曲线在达到最大应力后试样开始出现裂纹,应力开始降低,由于试样破裂形式存在不确定性,即使同一组试样的曲线降低部分也会存在较大差异,因此,本研究提出只计算曲线峰值(εb, σb)以前的包络面积,即试样开始出现裂纹前单位体积所吸收的能量,如图 2所示的阴影部分。因加载方式不同,可以计算出拉伸断裂能、压缩断裂能,计算公式分别见式(1)、式(2)。
|
图 2 以HMX为基炸药的典型拉伸、压缩σ-ε曲线 Fig.2 Typical tensile and compress σ-ε curves of HMX based explosive |
| $ {W_{\rm{t}}} = \int_0^{{\varepsilon _{\rm{b}}}} {{\sigma _{\rm{t}}}\left( \varepsilon \right){\rm{d}}\varepsilon } $ | (1) |
| $ {W_{\rm{c}}} = \int_0^{{\varepsilon _{\rm{b}}}} {{\sigma _{\rm{c}}}\left( \varepsilon \right){\rm{d}}\varepsilon } $ | (2) |
式中, Wt为拉伸断裂能,J·m-3,σt为拉伸应力,MPa,Wc为压缩断裂能,J·m-3,σc为压缩应力,MPa,ε为拉伸或压缩应变,εb为最大拉伸或压缩应力下的拉伸应变。
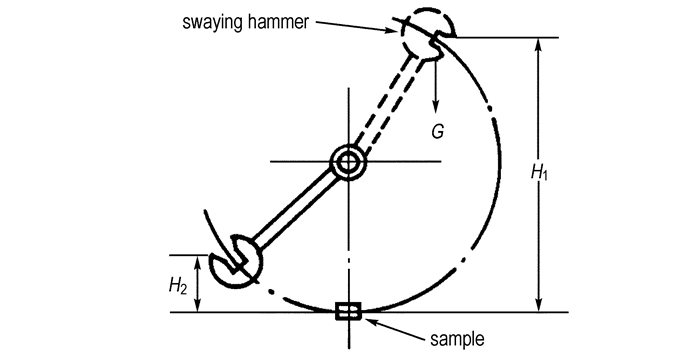
3 断裂能与冲击韧性、断裂韧性物理意义比较断裂能参量的物理意义是在机械载荷作用下,材料单位体积上吸收机械能量的大小,可以看出,该参量与材料韧性的定性表述的物理意义是相近的。而在材料韧性表征中最常用的冲击韧性参量Ak也是一种能量计算方法,冲击韧性Ak的测试原理如图 3所示。试验时将具有一定重量G的摆锤举至高度H1,使其具有一定势能,然后释放,在摆锤下落到最低位置处将试样冲断,摆锤损失一部分能量后上升到高度H2,根据H1与H2高度差,计算出试样吸收的能量并计算出Ak,见公式(3)[4]。尽管不能测试炸药冲击韧性,无法对炸药断裂能与冲击韧性相关性进行试验比较,但通过比较两种参量的测试原理可以发现,本研究提出的断裂能表征参量与冲击韧性具有相近的物理意义,只是断裂能采用的是静态加载方式,冲击韧性测试采用的是动态加载方式,可以推测,两者在测试值上应该具有较好的相关性。
|
图 3 冲击韧性测试原理示意图 Fig.3 Schematic diagram of impact toughness test |
| $ {{A}_{\rm{k}}}=\frac{G\left( {{H}_{1}}-{{H}_{2}} \right)}{BD} $ | (3) |
式中,Ak为冲击韧性,J·m-2; G为摆锤重量,N; H1为初始高度,m; H2为剩余高度,m; B为试样被冲断部位横截面的厚度,m; D为试样被冲断部位横截面的高度,m。
断裂韧性表征了材料抵抗裂纹扩展的能力,可采用三点弯曲试验进行测试,试样为矩形,其L为长度、B为厚度、D为高度、a为预制裂纹深度、S为跨距(图 4a)。采用材料试验机对试样进行静态加载至断裂,测试获得“负荷-裂纹开口位移”(P-V)曲线,PQ为P-V曲线中裂纹失稳扩展时的条件载荷,确定方法见图 4b,直线1是曲线起始部分的割线,直线2斜率是直线1斜率的95%,PQ为直线2与P-V曲线交点,Pm为最大载荷,断裂韧性测试要求Pm/PQ≤1.10[5]。最后根据公式(4)计算出断裂韧性KⅠC,公式中F(a/D)为裂纹深度与试样高度的函数[5]。

|
图 4 断裂韧性测试原理示意图 Fig.4 Schematic diagram of fracture toughness test |
| $ {{K}_{1\ \rm{C}}}=\frac{{{P}_{\mathit{Q}}}S}{B{{D}^{3/2}}}F\left( \frac{a}{D} \right) $ | (4) |
式中,KⅠC为断裂韧度,MPa·m1/2; PQ为条件载荷,N; S为跨距,m; B为试样厚度,m; D为试样高度,m; a为预制裂纹深度,m; F(a/D)为裂纹深度与试样高度的函数。
从断裂韧性的测试原理和计算方法看,断裂韧性的物理意义与本研究提出的断裂能显著不同。由于断裂韧性测试属于静态加载,试验安全,国内外已有对某HMX基炸药、某TATB基炸药的断裂韧性测试的文献报道[6-8],本研究将试验比较HMX基炸药(HMX-P1、HMX-P2)和TATB基炸药的断裂能与断裂韧性的相关性,试验包括:三种炸药材料常温下断裂能与断裂韧性比较, 其中一种HMX基炸药在不同温度下的断裂能与断裂韧性的变化规律比较。
4 试验条件 4.1 试样种类及尺寸试样材料种类及制备:炸药种类包括HMX基炸药(HMX-P1,HMX-P2)、TATB基炸药(TATB-P3)。
试样形状及尺寸:拉伸σt-ε曲线试样为Ф25 mm×65 mm圆哑铃,压缩σc-ε曲线试样为Ф20 mm×20 mm圆柱,KⅠC试样为80 mm×18 mm×9 mm,并预置裂纹深度为4.0 mm。每组试样数为3发。
4.2 仪器设备及试验条件仪器设备:INSTRON-5582电子万能试验机及其高低温环境试验箱。
试验温度:常温下HMX-P1、HMX-P2、TATB-P3的σ-ε曲线与KⅠC测试温度为20 ℃; 不同温度下HMX-P2的σ-ε曲线与KⅠC测试温度为20,35,45,60 ℃。
4.3 测试方法拉伸σt-ε曲线测试执行“GJB772A-1997方法417.1拉伸应力-应变曲线电子引伸计法”; 压缩σc-ε曲线测试执行“GJB772A-1997方法418.1压缩应力-应变曲线电子引伸计法”; 断裂韧性测试采用的测试装置见图 4、计算公式见式(4)。
5 试验结果与讨论 5.1 常温下三种炸药材料的断裂能与断裂韧性比较图 5是HMX-P1、HMX-P2、TATB-P3在常温下的拉伸σt-ε曲线、压缩σc-ε曲线以及P-V曲线。从测试曲线可以看出,TATB-P3与HMX-P1、HMX-P2存在显著差异,HMX-P1与HMX-P2差异较小。

|
图 5 3种炸药常温下的拉伸压缩σ-ε曲线与P-V曲线 Fig.5 Tensile σt-ε curves, compress σc-ε curves, P-V curves of three eplosives at room temperature |
根据图 5a、图 5b所示的三种炸药的拉伸与压缩σ-ε曲线,采用公式(1)、公式(2)计算了三种炸药的拉伸断裂能Wt和压缩断裂能Wc。根据图 5c,采用公式(4)计算获得三种炸药的断裂韧性KⅠC。计算结果见表 1,表 1中数据均为3发数据的平均值。从表 1可以看出三种炸药的断裂韧性存在一定差异,其中TATB-P3的断裂韧性值最大,表示该炸药的韧性相对较好,HMX-P1与HMX-P2的断裂韧性值接近,HMX-P1最小,表明HMX-P1的韧性最差。从计算结果来看,三种炸药的拉伸断裂能Wt、压缩断裂能Wc,都表现出与断裂韧性相同的变化规律,其中HMX-P1的拉伸、压缩断裂能最小,TATB-P3的拉伸、压缩断裂能最高。
| 表 1 三种炸药的断裂能与断裂韧性比较 Tab.1 Comparison of fracture energy and fracture toughness for three explosives |
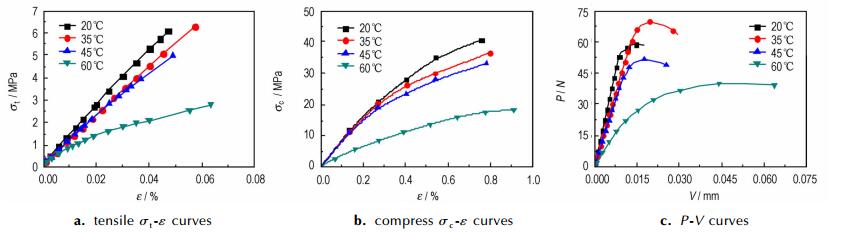
图 6是HMX-P2炸药在不同温度下的拉伸σt-ε曲线、压缩σc-ε曲线以及断裂韧性P-V测试曲线。由图 6可见,在20~60 ℃范围,随着温度增加,HMX-P2炸药三种曲线的斜率均有所降低,但是拉伸σt-ε曲线的最大应力值以及断裂韧性P-V测试曲线的最大载荷值均存在随温度升高开始增加而后降低的规律。
|
图 6 HMX-P2在不同温度下的拉伸、压缩σ-ε曲线和P-V曲线 Fig.6 Tensile σ-ε curves, compress σ-ε curves, P-V curves for HMX-P2 at different temperature |
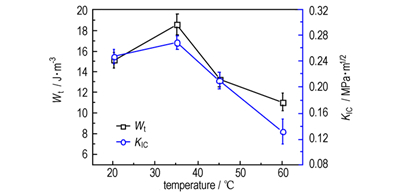
根据图 6a,图 6b所测试的HMX-P2炸药的拉伸、压缩σc-ε曲线,基于公式(1)、公式(2)计算了不同温度下HMX-P2的拉伸断裂能Wt和压缩断裂能Wc。根据图 6c,采用公式(4)计算获得HMX-P2在不同温度下的断裂韧度KⅠC。图 7是HMX-P2的拉伸断裂能Wt和压缩断裂能Wc与断裂韧性KⅠC变化趋势比较,总体来看,拉伸断裂能Wt、压缩断裂能Wc、断裂韧性KⅠC随温度变化趋势化存在较好一致性。当温度从20℃增加到35℃时,拉伸断裂能Wt、断裂韧性KⅠC均增大,压缩断裂能Wc略有降低,当着温度从35℃增加到60℃时,拉伸断裂能Wt、压缩断裂能Wc、断裂韧性KⅠC均随温度增加而降低。比较而言,拉伸断裂能Wt与断裂韧性KⅠC随温度变化趋势更好,这与断裂韧性测试时采用的三点弯曲试验与拉伸试验的加载方式有关。

|
图 7 HMX-P2的Wt、Wc与KⅠC随温度变化趋势比较 Fig.7 Comparison of Wt, Wc and KⅠC at for HMX-P2 |
基于以上对断裂能参量与冲击韧性测试原理的物理意义比较分析及三种炸药的断裂能与断裂韧性的变化趋势的试验对比,认为断裂能可以作为炸药的韧性表征参量。同时σ-ε曲线是炸药材料及成型技术研究中所必须进行的基本力学性能测试试验,该试验方法成熟而且容易实现,因此,本研究提出的基于σ-ε曲线能量计算的断裂能,可以在炸药增韧改性及成型技术研究中,作为韧性表征参量。
5 结论(1) 针对其他工程材料中常用的两种韧性参量(冲击韧性Ak、断裂韧性KⅠC)在表征炸药材料韧性时的局限性,提出了基于σ-ε曲线的断裂能量计算的韧性表征参量—断裂能,包括拉伸断裂能和压缩断裂能两种形式。
(2) 分析比较了断裂能与冲击韧性、断裂韧性这三个参量的物理意义,认为断裂能与冲击韧性具有相近物理意义。
(3) 试验比较了室温下HMX-P1,HMX-P2与TATB-P3这三种炸药材料之间的断裂能与断裂韧性差异,其中HMX-P1的断裂能和断裂韧性均最小,TATB-P3的断裂能和断裂韧性均最高; 同时还测试了HMX-P2在20, 35, 45, 60 ℃下的Wt,Wc,KⅠC,总体来看Wt、Wc、KⅠC随温度变化规律基本一致; 基于以上分析和对比试验, 认为基于σ-ε曲线断裂能量计算的断裂能可作为炸药的韧性表征参量。
| [1] |
Charles L Mader, Terry R Gibbs, Charles E Morris, et al. LASL explosive property data[M]. 1980.
|
| [2] |
董海山, 周芬芬.
高能炸药及相关物性能[M]. 北京: 科学出版社, 1989.
|
| [3] |
马卿, 舒远杰, 罗观, 等. TNT基熔铸炸药:增韧增弹的途径及作用[J].
含能材料, 2012, 20(5): 618-629. MA Qing, SHU Yuan-jie, LUO Guan, et al. Toughening and elasticizing route of TNT based melt cast explosives[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2012, 20(5): 618-629. |
| [4] |
梁光启, 林之为.
工程材料学[M]. 上海: 上海科学出版社, 1986.
|
| [5] |
崔振源.
断裂韧性测试原理和方法[M]. 上海: 上海科学技术出版社出版, 1981.
|
| [6] |
温茂萍, 马丽莲, 田勇, 等. 高聚物粘结炸药平面应变断裂韧度实验研究[J].
火炸药学报, 2001(2): 16-19. WEN Mao-ping, MA Li-lian, TIAN Yong, et al. Experimental study on the plane strain fracture toughness of high polymer bonded explosive[J]. Chinese Journal of Explosives & Propellants, 2001(2): 16-19. |
| [7] |
温茂萍, 庞海燕, 田勇, 等. PBX平面应变断裂韧度随温度的变化规律[J].
火炸药学报, 2005, 28(3): 63-65. WEN Mao-ping, PANG Hai-yan, TIAN Yong, et al. Regulations of plane strain fracture toughness of PBX changed with temperatures[J]. Chinese Journal of Explosives & Propellants, 2005, 28(3): 63-65. |
| [8] |
Louis Ferranti Jr, Franco J Gagliardi, Bruce J Cunningham, et al. Measure of quasi-static toughness and fracture parameters for mock explosive and insensitive high explosive LX17[C]//Proceedings of the 14th Symposium (International) on Detonation. 2010.
|
In order to solve the the limits of impact toughness Ak in characterization of explosive fracture toughness, the tensile fracture energy Wt and the compress fracture energy Wc based on the stress-strain curve were put forward. The similarity of the physical meanings between the fracture energy parameters(Wt,Wc)and the impact toughness Ak,was found via analyzing the test principle. Wt,Wc and KⅠC for different explosives HMX-P1,HMX-P2,TATB-P3 at room temperature were studied by experiments as well as for HMX-P2 at 20, 35, 45 ℃ and 60 ℃.



