中心抛撒药驱动固体、液体或固液混合物的抛撒技术,目前广泛应用于消防[1]、爆破除尘[2]和云雾爆轰[3]等领域。从起爆到壳体膨胀、破裂为破片的过程[4],以及燃料抛撒、碎解、雾化的过程[5],是爆轰驱动燃料抛撒[6]的两个外在表现形式。
试验研究[7-8]发现壳体结构在冲击下发生变形和断裂,其破片断面主要是由韧性剪切断裂造成的。裂纹由壳体外侧向内侧径向发展,当装药结构内部冲击压力大于壳体内表面张紧环所能承受的极限应力时,材料由塑性变形到完全断裂的情况就会发生[9]。也就是说在燃料从裂隙中泄压之前,装置结构对燃料的抛撒运动状态具有约束作用。因此适当减小壳体材料的屈服强度和厚度可提高燃料近场的抛撒速度[10]。除了削弱壳体的约束,增加中心抛撒药质量也可以达到相同的提高效果,但在一定范围内燃料抛散的最终云雾半径与抛撒药质量无关[11]。对于圆柱体装药结构,燃料在抛撒近场阶段的加速过程可认为是一维柱对称运动[12]。基于柱对称关系,张奇[13]推导了燃料近场抛撒最大速度的计算方法; Gardner[14-15]和Glass[16]构造了燃料抛撒的近场、远场以及近远场耦合模型,随后Singh[17]对近场模型进行了深化,研究了液滴的初始粒径分布; 丁珏[18-19]建立了抛撒近场阶段的初期一维单相流动模型和后期两相流数学模型,并给出了变质量运动边界的处理方法; 薛社生[20]利用有限差分程序模拟了远场的燃料抛散过程。
以往研究的装药结构多为圆柱体[21-22],而针对非圆截面壳体结构的燃料抛撒研究较少。与圆柱体结构不同,非圆截面壳体在外形上的不规则性,使其无法简化成单纯的柱对称模型。非圆截面装置在各个方向上的燃料抛撒初始速率和壳体应力分布是不同的。本研究针对一种扇形截面的装药结构,在中心抛撒药驱动下抛撒燃料的初始速率以及壳体的动态响应进行了数值模拟,并在试验结果对比的基础上,分析中心抛撒药类型及其位置、不同壳体刻槽形式对燃料抛撒的影响规律。
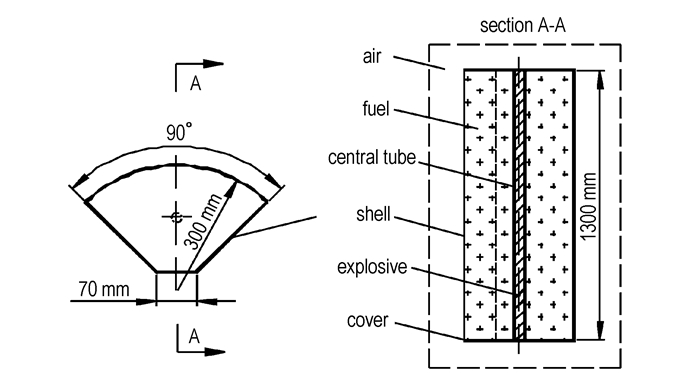
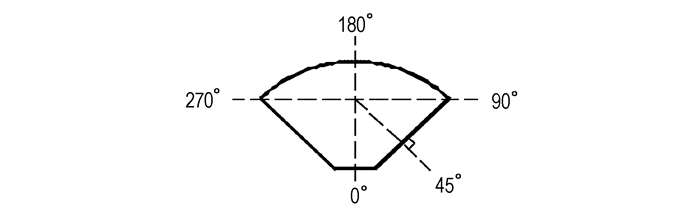
2 模拟参数 2.1 结构模型壳体的材料为铝,厚度为3mm,其结构横截面为扇形,模型与尺寸如图 1所示。抛撒药与弧线对应的圆心距离为185 mm。抛撒药的起爆位置为下端。模型中空气区域尺寸为1 m×1 m×2 m。空气域采用无反射边界条件。计算中采用流-固耦合算法[23]。壳体、中心管与端盖采用拉氏网格,抛撒药、燃料和空气采用欧拉网格。模型中的体单元形状为六面体,壳单元形状为四边形。单元总数量约为250万个,其中单元最大边长为15 mm,最小边长为1 mm。为描述方便,以几何形心为中心对壳体横截面进行方向标定,如图 2所示。外壳刻槽总数为18道,分别为0°方向2道,45°方向4道,180°方向8道,315°方向4道。刻槽间距为40 mm,刻槽深度为2 mm。
|
图 1 结构模型 Fig.1 Structure model |
|
图 2 方向示意 Fig.2 Direction view |
计算过程涉及的材料包括抛撒药、空气、燃料和壳体等物质。材料模型与数值取自文献[23-24]。抛撒药采用JWL状态方程,参数见表 1。
空气材料选用LINEAR_POLYNOMIAL状态方程。质量密度ρ为1.29×10-3 g·cm-3,单位体积内能E0为2.5×105 J·m-3,材料常数C4为0.4,C5为0.4。
燃料用水代替,采用GRUNEISEN状态方程。质量密度ρ为1.0 g·cm-3,材料常数C为1.65,S1为1.92,S2为-0.096,γ为0.35。
端盖材料为45#钢,选用PLASTIC_KINEMATIC模型。质量密度ρ为7.83 g·cm-3,弹性模量E为210 GPa,泊松比ν为0.3,屈服应力σs为0.355 GPa,屈服段模量Et为10 GPa,失效应变量δ为1.2。
中心管材料为25#钢,选用PLASTIC_KINEMATIC模型。质量密度ρ为7.83 g·cm-3,弹性模量E为210 GPa,泊松比ν为0.3,屈服应力σs为0.275 GPa,屈服段模量Et为10 GPa,失效应变量δ为0.8。
壳体材料为铝,选用PLASTIC_KINEMATIC模型。质量密度ρ为2.7 g·cm-3,弹性模量E为6 GPa,泊松比ν为0.3,屈服应力σs为0.262 GPa,屈服段模量Et为1 GPa,失效应变量δ为0.6。
为便于分析,针对分析对象做三点说明。第一,在燃料单元的选择方面,由于形成云雾的燃料抛撒方向主要为径向,且整体轴向中部横截面的燃料抛撒效果最为显著,因此在统计中仅对燃料中部横截面周边单元的水平方向抛撒速率进行分析。同时为降低随机误差,取某一单元及其相邻共5个单元的平均速率。第二,在抛撒速率的选取方面,根据燃料抛撒的近场特性并作为远场初始条件[26],选择最大速率作为分析数据。其主要原因是由于在壳体破坏后燃料开始出现剥离破碎,计算模型中使用的水状态方程显然已经不再适用。因此,需要将总计算时间控制在壳体破坏后的一定时间内。通过前期试算发现取总计算时长为2 ms时,模拟结果与试验情况较为相符。第三,在壳体破坏视角方面,考虑既展现全面观察壳体的破裂情况又节省篇幅,观测视角采用俯视。
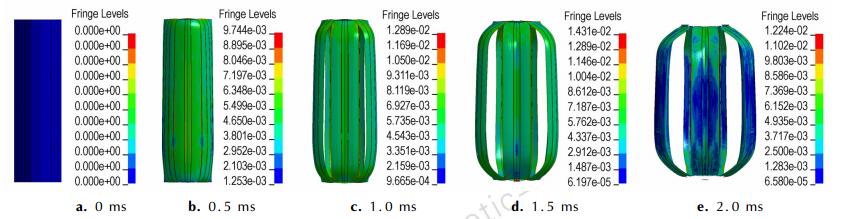
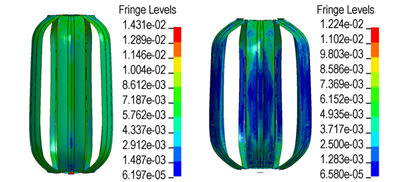
2.3 模拟与试验验证为了与试验验证中的高速摄像系统拍摄视角保持一致,针对模拟结果选取0°方向0~2 ms时刻对应的壳体响应过程,如图 3所示。其中抛撒药为梯恩梯(TNT)。
|
图 3 壳体应力模拟结果(×1011 Pa) Fig.3 Simulation results for shell stress(×1011 Pa) |
为了对数值模拟的可靠性进行验证,下面进行试验对比。试验的主要条件为:壳体下端板距离地面1.0 m。试验采用HG-100K高速摄像系统,以2000 fps的拍摄速度在0°方向进行图像采集,拍摄点与抛撒中心距离为100 m。试验中采集的燃料抛撒过程如图 4所示。

|
图 4 燃料抛撒与壳体破裂的试验结果 Fig.4 Experimental results for fuel dispersion and shell breakage |
由图 3和图 4可知,受到抛撒药下端起爆的影响,壳体下部最先出现外凸,0°~45°方向刻槽开裂,燃料沿着裂缝向外抛撒。由于计算中采用水的状态模型代替了试验中使用的燃料,因此导致二者在壳体破裂的均匀性方面略有差异。但总体上看,模拟结果与试验的壳体破裂趋势较为一致。
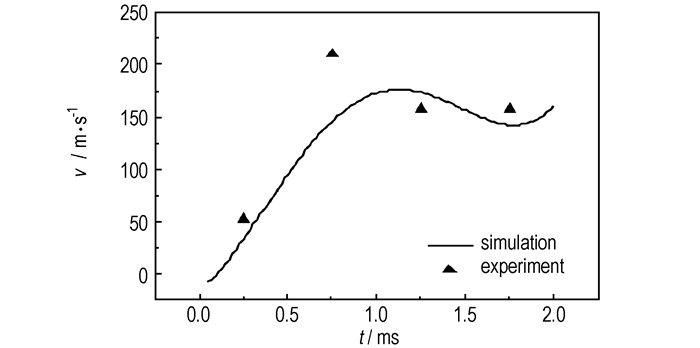
针对模拟与试验结果,将单侧燃料边界在水平方向的膨胀速率进行对比,如图 5所示。
|
图 5 边界速率的模拟结果与试验值对比 Fig.5 Comparison of edge velocity between simulation and experiment |
由图 5可知,在中心抛撒药的爆轰驱动下燃料边界迅速膨胀; 壳体材料在应力波作用下失效破裂燃料从裂隙中泄压,膨胀速率下降至150 m·s-1左右; 之后由于爆轰产物向外传播,边界膨胀速率又开始出现上升。模拟值与试验结果在总体趋势上是一致的,从而验证了数值模拟的正确性。
3 中心抛撒药的影响 3.1 抛撒药类型为研究中心抛撒药类型对抛撒效果的影响,分别针对相同质量的梯恩梯(TNT)、黑索今(RDX)和奥克托今(HMX)进行计算,具体参数见表 1。在中心抛撒药为TNT、与圆心距离为185 mm、刻槽间距为40 mm且刻槽深度为2 mm的条件下,计算得到各个方向的燃料速率时程曲线,图 6所示。在不同抛撒药条件下计算得到的燃料最大抛撒速率如图 7所示,壳体应力与破坏情况如图 8所示。
|
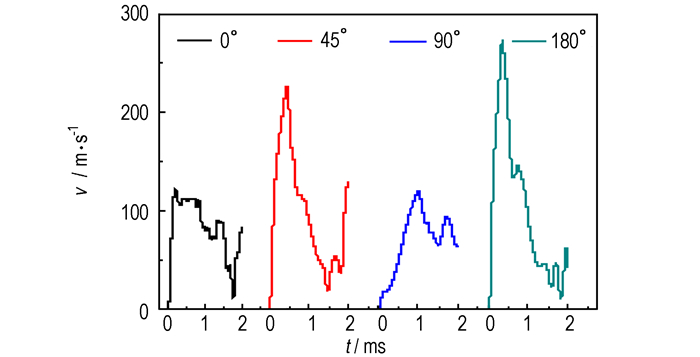
图 6 不同方向TNT的燃料抛撒速率时程曲线 Fig.6 Dispersal velocity of fuel vs time for TNT at different directions |
|
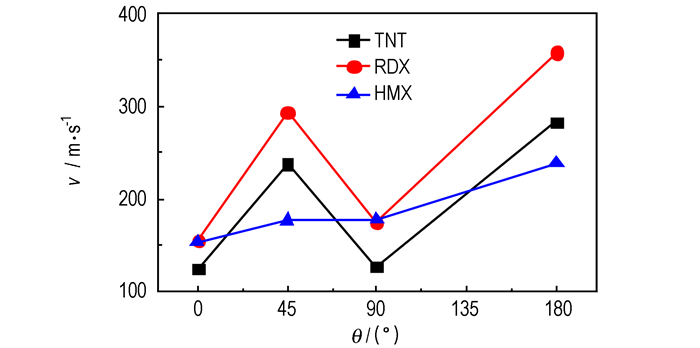
图 7 不同抛撒药条件下的抛撒燃料最大速率 Fig.7 Maximum dispersal velocity of fuel for different explosives |
|
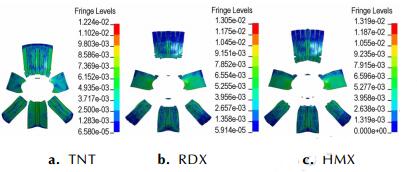
图 8 不同抛撒药条件下的壳体应力与破坏情况(2 ms,1×1011 Pa) Fig.8 Shell stress and breakage for different explosives(2 ms, 1×1011 Pa) |
由图 6可知,在中心抛撒药起爆后,燃料由静止开始加速,抛撒速率快速上升; 之后壳体受到应力波冲击并破裂,燃料泄压并受到空气阻力作用,燃料速率进入减速阶段。随着中心抛撒药产生的爆轰产物向外扩散推动燃料,燃料速率又有所上升。燃料的抛撒速率变化主要为先快速上升,后下降、振荡,再逐渐上升趋势。
在不同方向上的燃料最大速率不同,180°方向最大,45°方向其次,90°方向最小。最大速率出现时间上0°方向最早,45°和180°方向其次,90°方向最晚。这主要是由于冲击波达到各个方向最外层燃料的时刻以及壳体破裂的位置不同引起的。
由图 7可知,中心抛撒药对燃料初始抛撒速率的增强作用由大到小排序为RDX>TNT>HMX,而由图 8可知在壳体破裂的理想程度上排序为TNT>HMX>RDX。由此可见,低爆速、低爆压中心抛撒药驱动燃料抛撒的速率较低,但可保障壳体沿着预制刻槽破裂。适当提高抛撒药的爆速、爆压虽然给予了燃料较高的抛撒速率,但导致壳体出现横向断裂,加剧壳体的破坏(扭曲、碎片等)严重程度。而过高的能量密度使得壳体过早破裂,燃料的最大抛撒速率反而降低了,尤其是45°和180°方向。4个方向的抛撒速率平均下降18%。这可能是由于上述两个方向的壳体最先与冲击波相遇并破裂,而高爆速高爆压使得燃料从裂隙中泄压时间提前,燃料加速过程太短引起的。
3.2 抛撒药位置由于壳体结构的特殊性,针对不同抛撒药(中心管)位置进行计算。在平面几何层面上,若使得横截面被参考坐标轴分割的4个“子面积”均相等,那么抛撒药中心位置应为189.6 mm。因此取抛撒药中心与圆弧对应圆心的距离分别为175, 185, 195 mm共3种情况进行计算,获得4个方向燃料的最大速率如图 9所示,壳体应力与破坏情况如图 10所示。其中抛撒药为TNT,刻槽间距为40 mm,刻槽深度为2 mm。
|
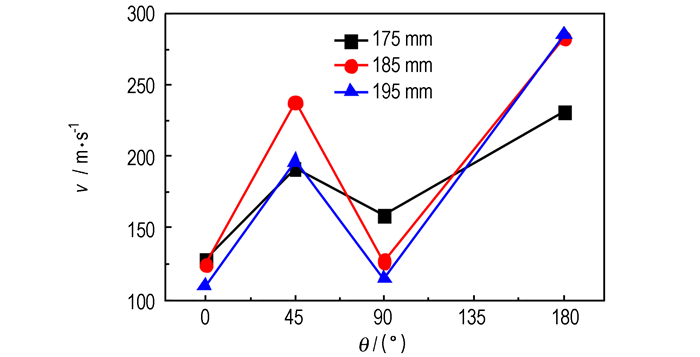
图 9 不同抛撒药中心与圆弧对应圆心的距离条件下的燃料最大速率 Fig.9 Maximum velocity of fuel for different distances between central explosive and circular center |

|
图 10 不同抛撒药中心与圆弧对应圆心的距离条件下的壳体应力与破坏情况(2 ms,1×1011 Pa) Fig.10 Shell stress and breakage for different distances between central explosive and circular center(2 ms, 1×1011 Pa) |
在0°方向3种计算条件下的速率为110~130 m·s-1。当抛撒药中心与圆弧对应圆心的距离为175 mm时,180°方向对应的速率最大,为231 m·s-1。随着距离的增加,抛撒药爆轰产生的冲击波到达0°和45°方向壳体的时刻也逐渐滞后,而到达180°和90°方向的时刻不断提前。与其他两种情况相比,距离为185 mm的计算值在4个方向的速率始终保持较高水平。当抛撒药中心与圆弧对应圆心的距离由185 mm增加为195 mm时,0°,45°和90°方向燃料最大速率减小,而180°方向燃料最大速率增大。
由图 10可知,在壳体破坏方面,随着抛撒药中心与圆弧对应圆心的距离的增加,45°和180°方向壳体横向断裂现象逐渐凸显。尤其当距离为195 mm时,0°方向壳体未沿着预制刻槽位置开裂。由此可见,抛撒药中心与壳体各个方向周边的距离差异不应过大。
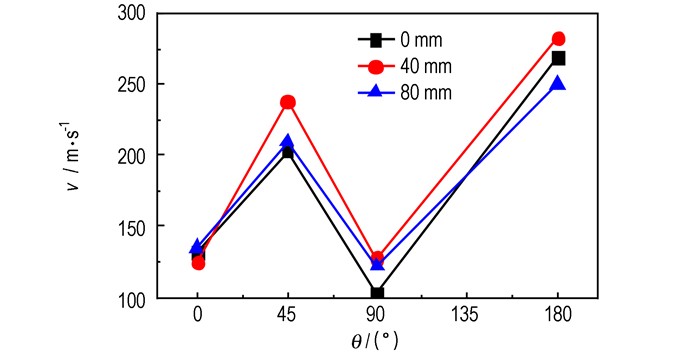
4 刻槽条件的影响 4.1 刻槽间距刻槽的主要目的是为了调整燃料的能量输出,便于燃料从预制刻槽产生的裂隙中泄压,同时避免壳体横向断裂引起燃料抛撒形成畸形云雾。下面分别针对刻槽间距为0 mm(无刻槽)、40 mm和80 mm共3种情况进行计算。其中抛撒药为TNT,抛撒药与圆弧对应圆心的距离为185 mm,刻槽深度为2 mm。获得4个方向燃料的最大速率如图 11所示,壳体应力与破坏情况如图 12所示。
|
图 11 不同刻槽间距条件下的燃料最大速率 Fig.11 Maximum velocity of fuel with different groove spacing for TNT |
|
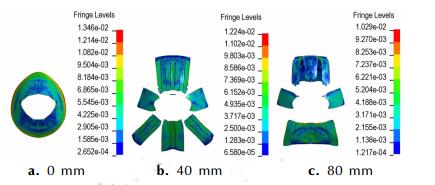
图 12 不同刻槽间距条件下的壳体应力与破坏情况(2 ms,1×1011 Pa) Fig.12 Shell stress and breakage with different groove spacing for TNT (2 ms, 1×1011 Pa) |
由图 11和图 12可知,当刻槽间距的不同时壳体破裂位置不同,无刻槽壳体不产生“条形”裂隙,不同方向上燃料的最大速率也相对较小,在180°方向的壳体出现了“尖端”,其附近的壳体受到的应力较大。在40 mm刻槽间距条件下,燃料抛撒最大速率较高,180°方向的速率为283 m·s-1。当刻槽间距为80 mm时,0°方向的壳体向内弯曲,180°方向的壳体产生2道失效裂隙。因此较小的刻槽间距能够为最终云雾区域内的燃料分布均匀性提供有利条件[21]。
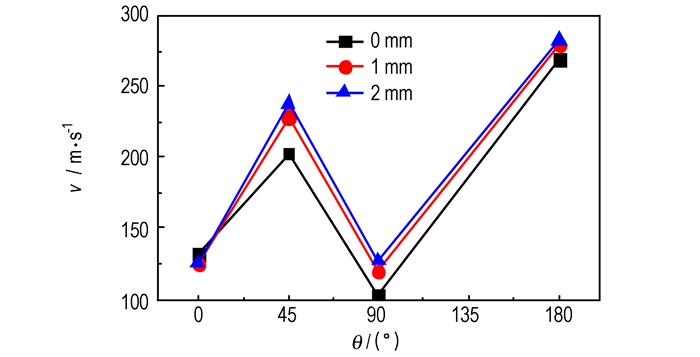
4.2 刻槽深度增加刻槽深度相当于削弱刻槽位置的壳体强度,从而使得壳体在冲击波作用下薄弱壳体处的破裂时刻提前。刻槽深度过小引起壳体在中心抛撒药驱动下发生不规则断裂; 刻槽深度过大则可能引起壳体失稳,并在燃料装填与保存过程中发生泄漏。考虑到壳体厚度为3 mm,针对刻槽深度分别为0 mm(无刻槽)、1 mm和2 mm共3种计算结果进行对比。其中抛撒药为TNT,抛撒药与圆弧对应圆心的距离为185 mm,刻槽间距为40 mm。4个方向燃料的最大速率如图 13所示,壳体应力与破坏情况如图 14所示。
|
图 13 不同刻槽深度条件下的燃料最大速率 Fig.13 The maximum velocity of fuel with different groove depth for TNT |
|
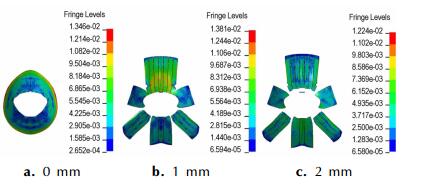
图 14 不同刻槽深度条件下的壳体应力与破坏情况(2 ms,1×1011 Pa) Fig.14 Shell stress and breakage with different groove depth for TNT(2 ms, 1×1011 Pa) |
由图 13可知,随着刻槽深度的减小,同一方向上的燃料抛撒速率逐渐降低(0°方向除外)。其中在90°方向速率降低至102 m·s-1。而由图 14可知当刻槽深度由2 mm降低至1 mm时,壳体形变量减小、0°方向壳体出现应力集中并局部横向断裂; 当刻槽深度为0 mm(无刻槽)时,壳体形变量进一步减小,且在2 ms计算范围内壳体未出现破裂。所以在不穿透壳体的前提下,较大的刻槽深度一方面对燃料抛撒最大速率起到增强作用,另一方面可减少壳体周边的应力集中。
5 结论本文基于有限元分析法,对扇形壳体结构的抛撒燃料过程进行了数值研究,主要结论如下:
(1) 在中心抛撒药的爆轰驱动下,燃料边界膨胀速率先快速上升,后小幅下降再重新上升。与试验结果对比发现,数值模拟结果符合实际情况。
(2) 不同中心抛撒药作用下,虽然壳体整体破坏趋势较为一致,但在能量密度过高的抛撒药驱动下燃料最大速率反而降低、壳体局部横向断裂以及和壳体碎片增多。另外,抛撒药的中心位置不应过度偏离横截面的几何形心。
(3) 无刻槽壳体在2 ms内未破裂且燃料速率较低,不利于燃料抛撒; 刻槽间距40 mm的计算结果优于80 mm和无刻槽情况。当刻槽间距40 mm且刻槽深度为2 mm时,壳体应力集中现象较少,且燃料在180°方向的最大速率为283 m·s-1。
| [1] |
Stefanski K, Lewandowski D, Dygdala R S, et al. Explosive formation and spreading of water-spray cloud-experimental development and model analyses[J].
Central European Journal of Energetic Materials, 2009, 6(3-4): 291-302. |
| [2] |
刘锋. 爆炸水雾降除爆破拆除粉尘的研究[D]. 淮南: 安徽理工大学, 2011.
LIU Feng. Research on blasting water mist reducing dust resulting from blasting demolition[D]. Huainan: Anhui University of Science and Technology, 2011. |
| [3] |
白春华, 梁慧敏, 李建平, 等.
云雾爆轰[M]. 北京: 科学出版社, 2012: 1-6.
|
| [4] |
张奇, 郭彦懿, 白春华, 等. 中心药量对燃料的抛散作用[J].
火炸药学报, 2001(1): 17-19. ZHANG Qi, GUO Yan-yi, BAI Chun-hua, et al. Dispersal affection of center high explosive charge to fuel[J]. Chinese Journal of Explosives & Propellants, 2001(1): 17-19. |
| [5] |
薛社生, 刘家骢, 彭金华. 液体燃料爆炸抛撒过程分析[J].
南京理工大学学报, 1998, 22(1): 34-38. XUE She-sheng, LIU Jia-cong, PENG Jin-hua. Analysis of explosive dispersion for liquid fuel[J]. Journal of Nanjing University of Science and Technology, 1998, 22(1): 34-38. |
| [6] |
薛社生, 刘家骢, 秦承森, 等. 燃料爆炸抛撒成雾的实验与数值研究[J].
爆炸与冲击, 2001, 21(4): 272-276. XUE She-sheng, LIU Jia-cong, QIN Cheng-sen, et al. Experimental and numerical investigation on explosive dispersal and cloud forming[J]. Explosion and Shock Waves, 2001, 21(4): 272-276. |
| [7] |
蒋治海, 龙新平, 韩勇, 等. 炸药爆炸驱动壳体破裂及液体喷射过程试验研究[J].
含能材料, 2011, 19(3): 321-324. JIANG Zhi-hai, LONG Xin-ping, HAN Yong, et al. Experimental studies on shell fracturing and jet forming and developing process driven by detonation[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2011, 19(3): 321-324. |
| [8] |
高重阳. 内部爆炸载荷下柱壳结构破裂问题的研究[D]. 北京: 清华大学, 2000.
GAO Chong-yang. Research on the rupture of cylindrical shell structure under internal explosive loading[D]. Beijing: Tsinghua University, 2000. |
| [9] |
Chester R H, Rodney F R. Fracture behavior of tubular bombs[J].
Journal of Applied Physics, 1968, 39(3): 1856-1862. DOI:10.1063/1.1656442 |
| [10] |
周保顺, 王少龙, 罗永锋, 等. 壳体对燃料近区抛撒速度影响的数值模拟[J].
火炸药学报, 2010, 33(2): 53-56. ZHOU Bao-shun, WANG Shao-long, LUO Yong-feng, et al. Numerical simulation on influence of shell on fuel near-field dispersal velocity[J]. Chinese Journal of Explosives & Propellants, 2010, 33(2): 53-56. |
| [11] |
张奇, 覃彬, 白春华, 等. 中心装药对FAE燃料成雾特性影响的试验分析[J].
含能材料, 2007, 15(5): 447-450. ZHANG Qi, QIN Bin, BAI Chun-hua, et al. Effection of total energy of center explosive charge on fuel dispersal characteristics feature[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2007, 15(5): 447-450. |
| [12] |
薛社生, 刘家骢, 彭金华. 液体燃料爆炸抛撒的近场阶段研究[J].
南京理工大学学报, 1997, 21(4): 333-336. XUE She-sheng, LIU Jia-cong, PENG Jin-hua. The Solution of near-field dispersion for liquid fuel FAE[J]. Journal of Nanjing University of Science and Technology, 1997, 21(4): 333-336. |
| [13] |
张奇, 白春华, 刘庆明, 等. 不耦合装药爆炸作用下燃料空气炸药的近区抛撒[J].
弹道学报, 2000, 12(2): 22-25. ZHANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Near field dispersal of FAE fuel under load of uncoupling charge in center pipe[J]. Journal of Ballistics, 2000, 12(2): 22-25. |
| [14] |
Gardner D R. Near-field Dispersal Modeling for Liquid Fuel-air-explosive[R]. Sandia National Laboratories Report, SAND90-0686, 1990.
|
| [15] |
Gardner D R, Glass M W. A Coupled near-field dispersal model for fuel-air-explosives[R]. Sandia National Laboratories Report, SAND90-0687, 1990.
|
| [16] |
Glass W M. Far-field Dispersal modeling for fuel-air-explosives[R]. Sandia National Laboratories Report, SAND90-0528, 1990.
|
| [17] |
Singh S K, Singh V. Extended near-field modeling and droplet size distribution for fuel-air explosive warhead[J].
Defence Science Journal, 2001, 51(3): 303-314. DOI:10.14429/dsj.51.2244 |
| [18] |
丁珏, 刘家骢, 彭金华. 液体燃料爆炸抛撒初期的一维数值模拟[J].
弹道学报, 1999, 11(3): 29-33. DING Jue, LIU Jia-cong, PENG Jin-hua. One-dimensional numerical simulation for the initial regime of liquid fuel explosive dispersal[J]. Journal o f Ballistics, 1999, 11(3): 29-33. |
| [19] |
丁珏, 刘家骢. 液体燃料爆炸抛撒和FAE形成过程的数值模拟[J].
南京理工大学学报, 2000, 24(2): 168-171. DING Jue, LIU Jia-cong. Numerical simulation on the process of explosive dispersal for forming FAE cloud[J]. Journal of Nanjing University of Science and Technology, 2000, 24(2): 168-171. |
| [20] |
薛社生. 液体燃料的爆炸抛撒研究[D]. 南京: 南京理工大学, 1997.
XUE She-sheng. Investigation of explosion dispersion for liquid fuels[D]. Nanjing: Nanjing University of Science and Technology, 1997. |
| [21] |
惠君明, 张陶, 郭学永. FAE装置参数对燃料抛撒与爆炸威力影响的实验研究[J].
高压物理学报, 2004, 18(2): 103-108. HUI Jun-ming, ZHANG Tao, GUO Xue-yong. Experimental study on the influence of device parameters of FAE to fuel dispersion and explosive power[J]. Chinese Journal of High Pressure Physics, 2004, 18(2): 103-108. DOI:10.11858/gywlxb.2004.02.006 |
| [22] |
郭学永. 云爆战斗部基础技术研究[D]. 南京: 南京理工大学, 2006.
GUO Xue-yong. Basic technical research on fuel air explosive warhead[D]. Nanjing: Nanjing University of Science and Technology, 2006. |
| [23] |
李裕春, 时党勇, 赵远.
ANSYS 11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008: 280-289.
|
| [24] |
白金泽.
LS-DYNA3D基础理论与实例分析[M]. 北京: 科学出版社, 2005: 89-100.
|
| [25] |
张宝钅平, 张庆明, 黄风雷.
爆轰物理学[M]. 北京: 兵器工业出版社, 2001: 160.
|
| [26] |
ZHANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Study on near field dispersal of fuel air explosive[J].
Journal of Beijing Institute of Technology, 1999, 8(2): 113-118. |
The processes of fuel dispersion and shell breakage driven by central explosive were simulated numericall by LS-DYNA program to study dispersal characteristics for sector cross-section structure. The simulated and experimental results were compared.



