高聚物粘结炸药(PBX)是由单质炸药与高聚物粘结剂组成的复合材料[1], 其具有能量高、机械感度低、力学性能和加工性能良好等特点, 被广泛应用于常规武器战斗部中[2]。PBX部件是供能部件, 在服役过程中可能会承载部分载荷, 当PBX部件经过载荷作用后会产生一系列内部裂纹, 裂纹的存在会引起结构强度和刚度下降, 并可能最终导致结构破坏[3]。对于PBX材料的力学性能和本构关系, 许多学者进行了一系列的实验与理论研究。
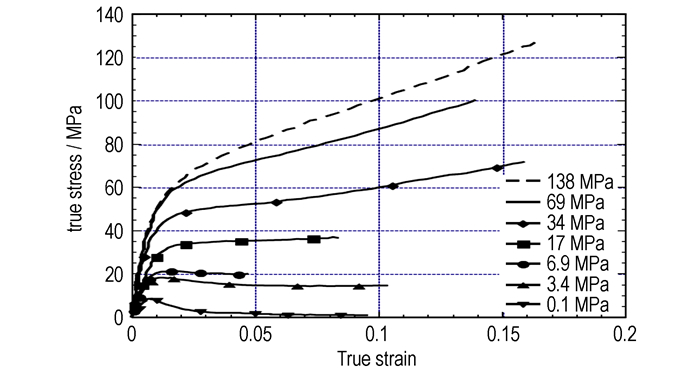
Belmas R[4]、K.ellis等[5]通过准静态单轴拉伸与单轴压缩实验研究发现了PBX材料的塑性硬化/软化特征, 并显示了特征中的所具有的拉压不对称性, 如图 1所示; Wiegand[6]、Asay等[7]等实验研究表明PBX力学性能受到静水压力的影响, 且其破坏强度随着静水压力的增加而增加, 如图 2所示; 温茂萍等[8]经过实验发现, 等静压炸药件的性能可以认为是各向同性的。

|
图 1 PBX的拉压不对称[10] Fig.1 Tension-compression asymmetry of PBX |
|
图 2 PBX受静水压力的影响[7] Fig.2 Influence of hydrostatic pressure in PBX |
罗景润[1]采用Ramberg-Osgood模型结合Johnson-Cook模型来描述PBX在拉伸加载状态下的本构关系, 引入了应变率和温度的影响, 获得了比较好的结果, 但是该模型在高应变率、压缩等状态下并不理想。李俊玲等[9]采用Sargin模型作为PBX的本构关系来研究应变率效应和温度效应在压缩加载状况下的影响, 其在压缩状态下能较好描述材料的弹性段与应变强化段, 但是并不能较好描述应变软化段, 也不能描述拉伸状态下的力学行为。以上两种本构模型在各自单一状态下描述较好, 但是并不能推广到复杂加载的状态, 也无法形成PBX三维本构模型。陈刚等[10]采用K & C模型模拟霍普金森压杆(SPHB)动态巴西圆盘试验, 其构造了屈服面与破坏面函数, 能描述比较复杂加载状态下的力学行为, 但其缺点在于因采用线性插值的方法而无法正确描述屈服面到破坏面之间的过程。吴艳青等[11]在研究PBX细观损伤时引入内聚力本构模型, 内聚力模型依赖于PBX组分之间的力学特性, 目前尚未得到广泛应用。郭虎等[12]采用Visco-SCRAM模型对PBX-9501的单轴拉伸、单轴压缩、应变率效应和粘性影响等进行了研究, 该模型能较好地反映PBX在单轴拉伸压缩下的力学行为和细观物理过程, 但是该模型所需参数很难获取。
PBX与岩石类准脆性材料具有材料强度与应力状态强烈相关的宏观特性, 也具有相类似的细观结构, 且均为颗粒类复合材料。相对而言, 混凝土的本构模型中关于应力状态对材料强度的描述相对要充分。在目前PBX本构模型研究中, 许多学者采用的Ramberg-Osgood模型、Sargin模型、K & C损伤模型等也是借鉴混凝土现有本构模型的。
Gruau等[13]在研究高能炸药低速冲击起爆过程中采用了Concrete Damage Plasticity模型来表征PBX的力学性能, 而该模型基于线性Drucker-Prager准则的, 表明该准则在预测PBX的力学行为方向有一定的意义, 但是由于目前这领域研究的比较少, 故在描述PBX材料的完整力学行为上尚需要更多的研究。
许多学者研究了Drucker-Prager准则在岩石力学方面的应用。余同希等[14]在研究复合材料环套混凝土的研究中对经典Drucker-Prager模型与线性Drucker-Prager模型的适用性进行了分析, 线性Drucker-Prager模型可以描述多种状态下的力学行为; 袁小平等[15]基于Drucker-Prager准则分析了岩土的硬化/软化特性, 提出了岩石的弹塑性损伤本构模型; 张艳山等[16]、刘金龙等[17]对Drucker-Prager系列准则的参数特性进行了讨论分析。与传统强度理论相比, Drucker-Prager系列准则既考虑了材料受静水压力影响的特性, 也考虑了材料拉压不同状态下力学性能不同的特性。
本研究基于PBX材料的力学性能及其材料特性与上述学者的研究结果, 采用线性Drucker-Prager模型对准静态承载下的PBX进行弹塑性分析以建立PBX的弹塑性本构模型。
2 线性Drucker-Prager模型线性Drucker-Prager模型是指描述试样加载过程中, 描述应变强化及软化段的模型。其完整模型由屈服面函数、流动势函数、破坏面函数等构成。其中, 线性Drucker-Prager模型的屈服面函数与破坏面函数都是由线性Drucker-Prager准则函数构成的。
2.1 屈服面函数线性Drucker-Prager准则由三个应力不变量表示, 屈服面函数的表达式为[18]:
| $ F = \frac{1}{2}q\left[ {1 + \frac{1}{K} - \left( {1 - \frac{1}{K}} \right){{\left( {\frac{r}{q}} \right)}^3}} \right] - p\tan \beta - d = 0 $ | (1) |
式中, p为等效围压应力, MPa; 其值为p=-
屈服面函数可用第一主应力不变量I1、第二偏应力不变量J2、第三偏应力不变量J3表示为
| $ F = \frac{1}{2}\sqrt {3{J_2}} \left( {1 + \frac{1}{K}} \right) - \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{{{J_3}}}{{{J_2}}} + \frac{1}{3}{I_1}\tan \beta - d = 0 $ | (2) |
则可知:
| $ \frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} = \frac{{\partial F}}{{\partial {I_1}}}\frac{{\partial {I_1}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} + \frac{{\partial F}}{{\partial {J_2}}}\frac{{\partial {J_2}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} + \frac{{\partial F}}{{\partial {J_3}}}\frac{{\partial {J_3}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} = {B_0}{\delta _{ij}} + {B_1}{s_{ij}} + {B_2}{t_{ij}} $ | (3) |
式中,
| $ \begin{array}{l} {B_0} = \frac{{\partial F}}{{\partial {I_1}}} = \frac{1}{3}\tan \beta ,\\ {B_1} = \frac{{\partial F}}{{\partial {J_2}}} = \frac{3}{{4\sqrt {3{J_2}} }}\left( {1 + \frac{1}{K}} \right) + \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{{{J_3}}}{{{{\left( {{J_2}} \right)}^2}}},\\ {B_2} = \frac{{\partial F}}{{\partial {J_3}}} = - \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{1}{{{J_2}}} \end{array} $ | (4) |
G为塑性流动势, 在线性模型中, 其表达式为[18]
| $ G = t - p\tan \varphi $ | (5) |
式中, φ为p-t平面上的剪胀角, (°); φ=0°时表示塑性变形材料的体积不发生变化; φ>0°, 材料发生剪胀效应。式(5)与式(1)的不同之处在于:式(1)中β为摩擦角, 式(5)中φ为剪胀角。
根据PBX材料承载实验中的体积膨胀效应的大小, 确定了采用非相关联流动法则(若采用相关联流动法则会高估PBX材料的体积膨胀)。
流动势函数可用第一主应力不变量I1、第二偏应力不变量J2、第三偏应力不变量J3表示为:
| $ G = \frac{1}{2}\sqrt {3{J_2}} \left( {1 + \frac{1}{K}} \right) - \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{{{J_3}}}{{{J_2}}} + \frac{1}{3}{I_1}\mathit{tan}{\rm{ \mathsf{ φ} }} $ | (6) |
则可知:
| $ \frac{{\partial }{\rm{G}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} = \frac{{\partial G}}{{\partial {I_1}}}\frac{{\partial {I_1}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} + \frac{{\partial G}}{{\partial {J_2}}}\frac{{\partial {J_2}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} + \frac{{\partial G}}{{\partial {J_3}}}\frac{{\partial {J_3}}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}} = {C_0}{\delta _{ij}} + {C_1}{s_{ij}} + {C_2}{t_{ij}} $ | (7) |
式中, C0、C1、C2为分量系数, 其值为:
| $ \begin{array}{l} {C_0} = \frac{{\partial G}}{{\partial {I_1}}} = \frac{1}{3}\tan \varphi ,\\ {C_1} = \frac{{\partial G}}{{\partial {J_2}}} = \frac{3}{{4\sqrt {3{J_2}} }}\left( {1 + \frac{1}{K}} \right) + \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{{{J_3}}}{{{{\left( {{J_2}} \right)}^2}}},\\ {C_2} = \frac{{\partial G}}{{\partial {J_3}}} = - \frac{9}{4}\left( {1 - \frac{1}{K}} \right)\frac{1}{{{J_2}}} \end{array} $ | (8) |
PBX在承载状态下, 总是先经历线弹性加载阶段, 达到初始屈服点后, 进入塑性流动加载段。根据温茂萍等[8]的研究结果, 认为PBX是各向同性的。
3.1 线弹性变形过程分析线弹性变形基于广义胡克定律, 其本构为[19]:
| $ {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}} = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} $ | (9) |
式中, σij为二阶张量表示的应力分量, εkl为二阶张量表示的应变分量, Cijkl为四阶张量表示的弹性矩阵。
对于各向同性的PBX材料, 其模型参数为杨氏模量E和泊松比ν, 剪切模量
| $ {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}} = G\left( {{\delta _{ik}}{\delta _{jl}} + {\delta _{il}}{\delta _{jk}} + \frac{{2V}}{{1 - 2V}}{\delta _{ij}}{\delta _{kl}}} \right) $ | (10) |
PBX加载过程中由线弹性段到达初始屈服点, 此时满足屈服准则, 之后进入塑性流动段, 之后一直处于屈服状态。
根据塑性理论, 总的应变增量[19]:
| $ {\rm{d}}{\varepsilon _{{\rm{ij}}}} = {\rm{d}}\varepsilon _{{\rm{ij}}}^{\rm{e}} + {\rm{d}}\varepsilon _{{\rm{ij}}}^{\rm{p}} $ | (11) |
相应的应力增量[19]:
| $ {\rm{d}}{\mathit{\boldsymbol{\sigma }}_{ij}} = {\mathit{\boldsymbol{C}}_{ijkl}}{\rm{d}}\varepsilon _{kl}^{\rm{e}} = {\mathit{\boldsymbol{\sigma }}_{ijkl}}\left( {{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{kl}} - {\rm{d}}\varepsilon _{kl}^p} \right) $ | (12) |
塑性流动法则[19]:
| $ {\rm{d}}\varepsilon _{{\rm{ij}}}^{\rm{p}} = {\rm{d}}\lambda \frac{{\partial G}}{{\partial {\sigma _{{\rm{ij}}}}}} $ | (13) |
根据流动法则, 可求得塑性流动段的泊松比为:
| $ {\nu _{\rm{p}}} = \left| {\frac{{{\rm{d}}\varepsilon _{11}^{\rm{p}}}}{{{\rm{d}}\varepsilon _{33}^{\rm{p}}}}} \right| = \left| {\frac{{{C_0}{\delta _{11}} + {C_1}{s_{11}} + {C_2}{t_{11}}}}{{{C_0}{\delta _{33}} + {C_1}{s_{33}} + {C_2}{t_{33}}}}} \right| $ | (14) |
假设等效塑性应变:
| $ {\rm{d}}{\varepsilon _{\rm{p}}} = C\sqrt {{\rm{d}}\varepsilon _{{\rm{ij}}}^{\rm{p}}{\rm{d}}\varepsilon _{{\rm{ij}}}^{\rm{p}}} = \varphi {\rm{d}}\lambda $ | (15) |
式中, C为等效塑性应变系数, 下同。联立(7)、(13)、(15)可得:
| $ \varphi = C\sqrt {\frac{{\partial G}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}\frac{{\partial G}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}} = C\sqrt {\left( {3C_0^2 + 2C_1^2{J_2} + 6{C_1}{C_2}{J_3} + \frac{8}{3}C_2^2{{\left( {{J_2}} \right)}^2}} \right)} $ | (16) |
根据一致性条件: dF=0, 联立(11)可知:
| $ \begin{array}{l} {\rm{d}}F = \frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}{\rm{d}}{\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}} + \frac{{\partial F}}{{\partial \tau }}\frac{{\partial \tau }}{{\partial {\varepsilon _{\rm{p}}}}}{\rm{d}}{\varepsilon _{\rm{p}}}\\ \;\;\;\;\; = \frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}\left( {{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} - {\rm{d}}\varepsilon _{kl}^{\rm{p}}} \right) + \frac{{\partial F}}{{\partial \tau }}{H^{\rm{p}}}{\rm{d}}{\varepsilon _{\rm{p}}} = 0 \end{array} $ | (17) |
式中, τ为应力形式的塑性内变量, 是等效塑性应变的函数;
将(12)、(13)代入(17), 联立(10)可得:
| $ \begin{array}{l} {\rm{d}}\lambda {\rm{ = }}\frac{1}{h}\frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}d{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}}\\ \;\;\;\; = \frac{{2G}}{h}\left( {{B_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\rm{d}}{\varepsilon _{{\rm{kk}}}} + {B_1}{s_{{\rm{kl}}}}{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} + {B_2}{t_{{\rm{kl}}}}{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}}} \right) \end{array} $ | (18) |
式中:
| $ \begin{array}{l} h = \frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}\frac{{\partial G}}{{\partial {\sigma _{{\rm{kl}}}}}} - {H^{\rm{p}}}\varphi \frac{{\partial F}}{{\partial \tau }}\\ = 2G\left( \begin{array}{l} 3{B_0}{C_0}\frac{{1 + \nu }}{{1 - 2\nu }} + 2{B_1}{C_1}{J_2} + 3{B_1}{C_2}{J_3}\\ + 3{B_2}{C_1}{J_3} + \frac{8}{3}{B_2}{C_2}{\left( {{J_2}} \right)^2} \end{array} \right) - {H^{\rm{p}}}\varphi \frac{{\partial F}}{{\partial \tau }} \end{array} $ | (19) |
根据塑性流动法则, 联立(13)、(18)可得:
| $ {\rm{d}}\varepsilon _{{\rm{mn}}}^{\rm{p}} = {\rm{d}}\lambda \frac{{\partial G}}{{\partial {\sigma _{{\rm{mn}}}}}} = \left( {\frac{1}{h}\frac{{\partial F}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}}} \right)\frac{{\partial }{\rm{G}}}{{\partial {{\rm{ \mathsf{ σ} }}_{{{mn}}}}}} $ | (20) |
联立(12)、(20), 可得应力增量:
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}} = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}{\rm{d}}\varepsilon _{{\rm{kl}}}^{\rm{e}} = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}\left( {{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} - {\rm{d}}\varepsilon _{{\rm{kl}}}^{\rm{p}}} \right)\\ \;\;\;\;\;\; = {C_{{\rm{ijrs}}}}{\rm{d}}{\varepsilon _{{\rm{rs}}}} - {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}\left( {\frac{1}{h}\frac{{\partial F}}{{\partial {\sigma _{{\rm{pq}}}}}}{C_{{\rm{pqrs}}}}{\rm{d}}{\varepsilon _{{\rm{rs}}}}} \right)\frac{{\partial G}}{{\partial {\sigma _{{\rm{kl}}}}}}\\ \;\;\;\;\;\; = \left( {{C_{{\rm{ijrs}}}} - \frac{1}{h}\frac{{\partial F}}{{\partial {\sigma _{{\rm{pq}}}}}}{C_{{\rm{pqrs}}}}{C_{{\rm{ijrs}}}}\frac{{\partial G}}{{\partial {\sigma _{{\rm{rs}}}}}}} \right){\rm{d}}{\varepsilon _{{\rm{rs}}}}\\ \;\;\;\;\;\; = \left( {{C_{{\rm{ijrs}}}} + C_{{\rm{ijrs}}}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{{\rm{rs}}}} = C_{{\rm{ijrs}}}^{{\rm{ep}}}{\rm{d}}{\varepsilon _{{\rm{rs}}}} \end{array} $ | (21) |
式中,
| $ \begin{array}{l} C_{{\rm{ijrs}}}^{\rm{p}} = - \frac{1}{h}H_{{\rm{ij}}}^ * {H_{{\rm{rs}}}},\\ H_{{\rm{ij}}}^ * = {C_{{\rm{ijmn}}}}\frac{{\partial G}}{{\partial {\sigma _{{\rm{mn}}}}}} = 2G\left( {{C_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{ij}}}} + {C_1}{\delta _{{\rm{ij}}}} + {C_2}{t_{{\rm{ij}}}}} \right),\\ {H_{{\rm{rs}}}} = {C_{{\rm{rsmn}}}}\frac{{\partial F}}{{\partial {\sigma _{{\rm{mn}}}}}} = 2G\left( {{B_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{rs}}}} + {B_1}{s_{{\rm{rs}}}} + {B_2}{t_{{\rm{rs}}}}} \right) \end{array} $ | (22) |
可得:
| $ \begin{array}{l} C_{{\rm{ijkl}}}^{\rm{p}} = - \frac{1}{h}H_{{\rm{ij}}}^ * {H_{{\rm{kl}}}}\\ \;\;\;\;\;\; = - \frac{{4{G^2}}}{h}\left( {{C_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{ij}}}} + {C_1}{s_{{\rm{ij}}}} + {C_1}{t_{{\rm{ij}}}}} \right)\left( {{B_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{kl}}}} + {B_1}{s_{{\rm{kl}}}} + {B_2}{t_{{\rm{kl}}}}} \right) \end{array} $ | (23) |
对于给定的位移加载, 转换成应变增量, 根据(10)、(23)即可计算出PBX的弹塑性本构关系:
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}} = \left( {{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}} + C_{{\rm{ijkl}}}^{\rm{p}}} \right){\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} = \left( {G\left( {{\delta _{{\rm{ik}}}}{\delta _{{\rm{jl}}}} + {\delta _{{\rm{il}}}}{\delta _{{\rm{jk}}}} + \frac{{2V}}{{1 - 2V}}{\delta _{{\rm{ij}}}}{\delta _{{\rm{kl}}}}} \right) - } \right.\\ \;\;\;\;\;\;\left. {\frac{{4{G^2}}}{h}\left( {{C_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{ij}}}} + {C_1}{s_{{\rm{ij}}}} + {C_2}{t_{{\rm{ij}}}}} \right)\left( {{B_0}\frac{{1 + \nu }}{{1 - 2\nu }}{\delta _{{\rm{kl}}}} + {B_1}{s_{{\rm{kl}}}} + {B_2}{t_{{\rm{kl}}}}} \right)} \right){\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\mathit{\boldsymbol{kl}}}} \end{array} $ | (24) |
采用笛卡尔坐标系对PBX单元体受单轴位移加载作用的弹塑性变形进行分析。
现采用文献[13]中由尺寸200 μm左右的HMX颗粒和少量高分子粘结剂等经一定工艺等压压缩而成的某种PBX(力学特性类似于PBX-9501), 其力学性能相关数据: E=4 GPa, K=1, v=0.4, β=20°, φ=1°, 采用单轴压缩下的硬化数据,
单轴压缩状态下, 可知: σ11=σ22=0>σ33=σcy, 其他应力分量也为零。σcy为屈服后的压应力, MPa。
可求得:
| $ \begin{array}{l} {s_{11}} = {s_{22}} = - \frac{1}{3}{\sigma _{{\rm{cy}}}},{s_{33}} = \frac{2}{3}{\sigma _{{\rm{cy}}}};\\ {t_{11}} = {t_{22}} = - \frac{1}{9}\sigma _{{\rm{cy}}}^2,{t_{33}} = \frac{2}{9}\sigma _{{\rm{cy}}}^2;\\ {I_1}{\rm{ = }}{\sigma _{{\rm{cy}}}},{J_2} = \frac{1}{3}\sigma _{{\rm{cy}}}^2,{J_3} = \frac{2}{{27}}\sigma _{{\rm{cy}}}^3 \end{array} $ | (25) |
根据单轴压缩状态下dεp=-dε33p, 联立(13)、(15)可求得:
| $ C = \frac{{\left| {\frac{{\partial G}}{{\partial {\mathit{\sigma }_{{\rm{33}}}}}}} \right|}}{{\sqrt {\frac{{\partial G}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}\frac{{\partial G}}{{\partial {\mathit{\boldsymbol{\sigma }}_{\mathit{\boldsymbol{ij}}}}}}} }} = 0.8117,\varphi = 1 - \frac{1}{3}\tan \varphi = 0.9942 $ | (26) |
将单轴压缩状态的应力关系代入(4)、(8)等可得:
| $ \begin{array}{l} {B_0} = \frac{1}{3}\tan \beta ,{B_1} = - \frac{3}{{2{\sigma _{{\rm{cy}}}}}},{B_2} = 0;\\ {C_0} = \frac{1}{3}\tan \varphi ,{C_1} = - \frac{3}{{2{\sigma _{{\rm{cy}}}}}},{C_2} = 0 \end{array} $ | (27) |
由v=0.4可知在单轴压缩状态下:
| $ {\rm{d}}{\varepsilon _{11}} = {\rm{d}}{\varepsilon _{22}} = - 0.4{\rm{d}}{\varepsilon _{33}} $ | (28) |
其加载过程中, 本构关系如下
弹性加载段:
| $ \begin{array}{l} {\rm{d}}{\sigma _{33}} = {C_{3311}}{\rm{d}}{\varepsilon _{11}} + {C_{3322}}{\rm{d}}{\varepsilon _{22}} + {C_{3333}}{\rm{d}}{\varepsilon _{33}}\\ \;\;\;\;\;\;\; = 2.8{\rm{Gd}}{\varepsilon _{33}} = {\rm{Ed}}{\varepsilon _{33}} \end{array} $ | (29) |
塑性加载段:
| $ \begin{array}{l} {\rm{d}}{\sigma _{33}} = \left( {{C_{3311}} + C_{3311}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{11}} + \left( {{C_{3322}} + C_{3322}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{22}} + \\ \;\;\;\;\;\;\;\;\;\;\left( {{C_{3333}} + C_{3333}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{33}} \end{array} $ | (30) |
将数据代入(14)方程, 可得:
| $ {\nu _p} = \left| {\frac{{{\rm{d}}\varepsilon _{11}^{\rm{p}}}}{{{\rm{d}}\varepsilon _{33}^{\rm{p}}}}} \right| = \left| {\frac{{{C_0}{\delta _{11}} + {C_1}{s_{11}}}}{{{C_0}{\delta _{33}} + {C_1}{s_{33}}}}} \right| = \left| {\frac{{\frac{1}{3}\tan \varphi + \frac{1}{2}}}{{\frac{1}{3}\tan \varphi - 1}}} \right| = 0.5088 $ | (31) |
将数据代入(19)式, 可得
| $ h = \frac{{\partial F}}{{\partial {\sigma _{{\rm{ij}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{ijkl}}}}}}\frac{{\partial G}}{{\partial {\sigma _{{\rm{kl}}}}}} - {H^p}\varphi \frac{{\partial F}}{{\partial \tau }} = 3.0296{\rm{G}} + 0.8736{H^{\rm{p}}} $ | (32) |
将数据代入(23)式, 可得
| $ C_{3333}^{\rm{p}} = - \frac{1}{h}H_{33}^ * {H_{33}} = - \frac{{0.5784{G^2}}}{{3.0296{\rm{G}} + 0.8736{H^{\rm{p}}}}} $ | (33) |
同理可得:
| $ C_{3311}^{\rm{p}} = C_{3322}^{\rm{p}} = \frac{{5.1772{G^2}}}{h} = \frac{{5.1772{G^2}}}{{3.0296{\rm{G}} + 0.8736{H^{\rm{p}}}}} $ | (34) |
联立(30)、(31)、(32)、(33)、(34), 可计算得:
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{\sigma }}_{33}} = \left( {{C_{3311}} + C_{3311}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{11}} + \left( {{C_{3322}} + C_{3322}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{22}} + \\ \left( {{C_{3333}} + C_{3333}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{33}} = {\rm{d}}{\sigma _{33}} + \left( { - 0.4C_{3311}^{\rm{p}} - 0.4C_{3322}^{\rm{p}} + C_{3333}^{\rm{p}}} \right){\rm{d}}\varepsilon _{33}^{\rm{e}} + \\ \left( { - 0.5088\left( {{C_{3311}} + C_{3311}^{\rm{p}}} \right) - 0.5088\left( {{C_{3322}} + C_{3322}^{\rm{p}}} \right) + \left( {{C_{3333}} + C_{3333}^{\rm{p}}} \right)} \right)\\ {\rm{d}}\varepsilon _{33}^{\rm{p}} = {\rm{d}}{\sigma _{33}} - \frac{{4.7202G}}{h}{\rm{d}}\varepsilon _{33}^{\rm{e}} + \left( {1.9298G - \frac{{5.8465G}}{{\rm{h}}}} \right){\rm{d}}\varepsilon _{33}^{\rm{p}} \end{array} $ | (35) |
即
| $ \begin{array}{l} {\rm{d}}\varepsilon _{33}^{\rm{e}} = \frac{{1.9298{\rm{h}} - 5.8465{\rm{G}}}}{{4.7202{\rm{G}}}}{\rm{d}}\varepsilon _{33}^{\rm{p}}\\ = \frac{{1.9298\left( {3.0296{\rm{G}} + 0.8736{{\rm{H}}^{\rm{p}}}} \right) - 5.8465G}}{{4.7202{\rm{G}}}}{\rm{d}}\varepsilon _{33}^{\rm{p}}\\ = \frac{{0.3571{H^{\rm{p}}}}}{{\rm{G}}}{\rm{d}}\varepsilon _{33}^{\rm{p}} \end{array} $ | (36) |
联立(36), 可得:
| $ {\rm{d}}{\sigma _{33}} = 2.8G{\rm{d}}\varepsilon _{33}^{\rm{e}} = {H^{\rm{p}}}{\rm{d}}\varepsilon _{33}^{\rm{p}} = \frac{{G{H^{\rm{p}}}}}{{0.3571{H^{\rm{p}}} + G}}{\rm{d}}{\varepsilon _{33}} $ | (37) |
显然, 根据
| $ {\rm{d}}\left| {{\sigma _{33}}} \right| = {H^{\rm{p}}}{\rm{d}}\left| {\varepsilon _{33}^{\rm{p}}} \right| = 2.8G{\rm{d}}\left| {\varepsilon _{33}^{\rm{e}}} \right| = \frac{{2.8G{H^{\rm{p}}}}}{{{H^{\rm{p}}} + 2.8G}}{\rm{d}}\left| {{\varepsilon _{33}}} \right| $ | (38) |
至此, 可知式(37)与(38)是一致的, 故单轴压缩下, PBX塑性阶段本构关系即为(37), 取决于单轴压缩塑性硬化/软化参数Hp。
4.2 双轴压缩算例分析方法与单轴压缩状态类似, 采用的数据也源于文献[13]。
对于双轴压缩, 则其受力情况: σ11=0>σ22=σ33=σcy, 其他应力分量为零。
| $ \begin{array}{l} {s_{11}} = - \frac{2}{3}{\sigma _{{\rm{cy}}}},{s_{22}} = {s_{33}} = \frac{1}{3}{\sigma _{{\rm{cy}}}};\\ {t_{11}} = \frac{2}{9}\sigma _{{\rm{cy}}}^2,{t_{22}} = {t_{33}} = - \frac{1}{9}\sigma _{{\rm{cy}}}^2;\\ {I_1} = 2{\sigma _{{\rm{cy}}}},{J_2} = \frac{1}{3}\sigma _{{\rm{cy}}}^2,{J_3} = - \frac{2}{{27}}\sigma _{{\rm{cy}}}^3 \end{array} $ | (39) |
C, φ的值, 由硬化形式决定, 屈服函数采用单轴压缩硬化数据, 故其与单轴压缩状态下一致, 即: C=0.8117, φ=0.9942
结合模拟条件, K=1, v=0.4, β=20°, φ=1°,
| $ \begin{array}{l} {B_0} = \frac{1}{3}\tan \beta ,{B_1} = - \frac{3}{{2{\sigma _{\rm{c}}}}},{B_2} = 0;\\ {C_0} = \frac{1}{3}\tan \varphi ,{C_1} = - \frac{3}{{2{\sigma _{\rm{c}}}}},{C_2} = 0 \end{array} $ | (40) |
由v=0.4, 可知双轴压缩状态下: dε11=-1.3333dε22=-1.3333dε33
故弹性加载段:
| $ \begin{array}{l} {\rm{d}}{\sigma _{33{\rm{b}}}} = {C_{3311}}{\rm{d}}{\varepsilon _{11{\rm{b}}}} + {C_{3322}}{\rm{d}}{\varepsilon _{22{\rm{b}}}} + {C_{3333}}{\rm{d}}{\varepsilon _{33{\rm{b}}}}\\ = \left( { - 1.3333{C_{3311}} + {C_{3322}} + {C_{3333}}} \right){\rm{d}}{\varepsilon _{33{\rm{b}}}} = 4.6667{\rm{d}}{\varepsilon _{33{\rm{b}}}} \end{array} $ | (41) |
将数据代入(19)式, 可得:h=3.0296G+0.8736Hp,
将数据代入(23)式, 可得
| $ \begin{array}{l} C_{3311}^{\rm{p}} = - \frac{1}{h}H_{33}^ * {H_{11}}\\ = - \frac{{4{G^2}}}{h}\left( {{C_0}\frac{{1 + v}}{{1 - 2v}}{\delta _{33}} + {C_1}{s_{33}} + {C_2}{t_{33}}} \right)\left( {{B_0}\frac{{1 + v}}{{1 - 2v}}{\delta _{11}} + {B_1}{s_{11}} + {B_2}{t_{11}}} \right)\\ = \frac{{3.3973{{\rm{G}}^2}}}{{3.0296{\rm{G}} + {\rm{0}}{\rm{.8736}}{H^{\rm{p}}}}} \end{array} $ | (42) |
同理可得:
| $ C_{3322}^{\rm{p}} = C_{3322}^{\rm{p}} = \frac{{0.6416{{\rm{G}}^2}}}{h} = \frac{{0.6416{{\rm{G}}^2}}}{{3.0296{\rm{G}} + {\rm{0}}{\rm{.8736}}{H^{\rm{p}}}}} $ | (43) |
双轴压缩状态下的塑性泊松比为:
| $ {\nu _{\rm{p}}} = \left| {\frac{{{\rm{d}}\varepsilon _{11{\rm{b}}}^{\rm{p}}}}{{{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}}}} \right| = \left| {\frac{{{C_0}{\delta _{11}} + {C_1}{s_{11}}}}{{{C_0}{\delta _{33}} + {C_1}{s_{33}}}}} \right| = \left| {\frac{{\frac{1}{3}\tan \varphi + 1}}{{\frac{1}{3}\tan \varphi - \frac{1}{2}}}} \right| = 2.0353 $ | (44) |
故可知塑性加载段的特征:
| $ \begin{array}{l} {\rm{d}}{\mathit{\boldsymbol{\sigma }}_{33{\rm{b}}}} = \left( {{C_{3311}} + C_{3311}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{11{\rm{b}}}} + \left( {{C_{3322}} + C_{3322}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{22{\rm{b}}}} + \\ \left( {{C_{3333}} + C_{3333}^{\rm{p}}} \right){\rm{d}}{\varepsilon _{33{\rm{b}}}} = {\rm{d}}{\sigma _{33b}} + \left( { - 1.3333C_{3311}^{\rm{p}} + C_{3322}^{\rm{p}} + C_{3333}^{\rm{p}}} \right){\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{e}} + \\ \left( { - 2.0353\left( {{C_{3311}} + C_{3311}^{\rm{p}}} \right) + \left( {{C_{3322}} + C_{3322}^{\rm{p}}} \right) + \left( {{C_{3333}} + C_{3333}^{\rm{p}}} \right)} \right){\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}\\ = {\rm{d}}{\sigma _{33{\rm{b}}}} - \frac{{3.2465{\rm{G}}}}{h}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{e}} + \left( {1.8588{\rm{G}} - \frac{{5.6313{\rm{G}}}}{h}} \right){\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}} \end{array} $ | (45) |
由(45)可得:
| $ \begin{array}{l} {\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{e}} = \frac{{1.8588h - 5.6316{\rm{G}}}}{{3.2465{\rm{G}}}}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}\\ \;\;\;\;\;\;\;\; = \frac{{1.8588\left( {3.0296{\rm{G}} + 0.8736{H^{\rm{p}}}} \right) - 5.6316{\rm{G}}}}{{3.2465{\rm{G}}}}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}\\ \;\;\;\;\;\;\;\; = \frac{{0.5002{H^{\rm{p}}}}}{G}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}} \end{array} $ | (46) |
| $ \begin{array}{l} {\rm{d}}{\sigma _{33{\rm{b}}}} = 4.6667G{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{e}} = 2.3342{H^{\rm{p}}}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}\\ \;\;\;\;\;\;\;\; = \frac{{2.3342G{H^{\rm{p}}}}}{{0.5002{H^{\rm{p}}} + G}}{\rm{d}}{\varepsilon _{33{\rm{b}}}} \end{array} $ | (47) |
式(47)即为双轴压缩状态下的塑性本构。
根据流动法则, 可知双轴压缩下dε33bp与单轴压缩下的dε33p之比为:
| $ \frac{{{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}}}{{{\rm{d}}\varepsilon _{33}^{\rm{p}}}} = \frac{{\frac{1}{3}\tan \varphi - \frac{1}{2}}}{{\frac{1}{3}\tan \varphi - 1}} = 0.4971 $ | (48) |
联立(47)、(48), 可得:
| $ \begin{array}{l} {\rm{d}}{\sigma _{33b}} = 4.6667G{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{e}} = 2.3342{H^{\rm{p}}}{\rm{d}}\varepsilon _{33{\rm{b}}}^{\rm{p}}\\ \;\;\;\;\;\;\;\; = 1.1603{H^{\rm{p}}}{\rm{d}}\varepsilon _{33}^{\rm{p}} \end{array} $ | (49) |
故理论上可得, 双轴压缩与单轴压缩的极限强度之比为:
| $ \frac{{{\sigma _{33{\rm{b}}}}}}{{{\sigma _{33}}}} = \frac{{{\rm{d}}{\sigma _{33{\rm{b}}}}}}{{{\rm{d}}{\sigma _{33}}}} = 1.16 $ | (50) |
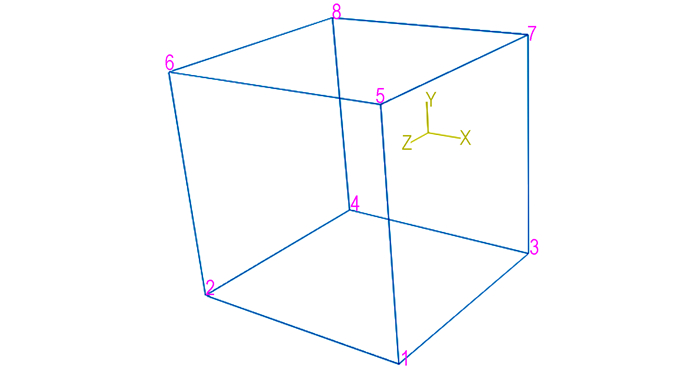
采用Abaqus中线性Drucker-Prager模型来表征材料特性, 材料参数为文献[13]中的PBX参数: E=4 GPa, K=1, v=0.4, β=20°, φ=1°, 其硬化特性数据来源于单轴压缩下的实验数据, 如表 1所示。因重点研究材料的本构关系, 故分析时只取一个单元进行数值模拟分析, 单元类型为八节点等参缩减积分单元C3D8R, 单元尺寸为0.2 mm×0.2 mm×0.2 mm, 如图 3所示。
| 表 1 单轴压缩下的PBX塑性硬化数据[10] Tab.1 Plastic hardening data of PBX in uniaxial compression |
|
图 3 有限元单元及其节点符号 Fig.3 Element and node symbols of FEM |
边界条件:面1562、面3784、面1573和面2684不受约束, 面1342固定以控制刚体位移, 面5786受到与该面法向方向相同的压缩强制位移, 位移量为0.02 mm。加载控制方式为位移线性加载。
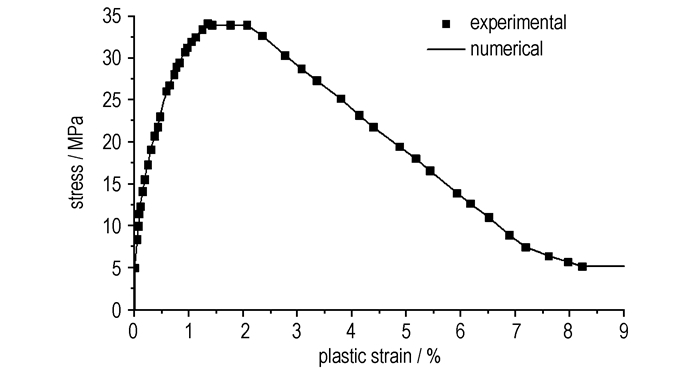
分析数值模拟的结果, 为了便于与实验数据相对应, 选取压缩状态下等效应力与等效塑性应变曲线进行比较, 如图 4所示。由图 4可以看出, 数值模拟的结果与实验结果吻合得非常好, 验证了基于线性Drucker-Prager模型的数值模拟结果取决于塑性硬化数据的特征, 这结论与理论上的弹塑性变形分析结果(38)式结论一致; 同时, 可以看出, 该PBX在加载过程中先后经历了塑性硬化与塑性软化过程才完全破坏, 其极限强度为34.04 MPa, 此时对应塑性应变为1.38%, 此时的总应变为2.23%, 这与大多数PBX材料在常温下的准静态单轴压缩实验结果相似; 同时可以分析出:在极限强度处, 即开始出现破坏现象时, 其应力变化不如应变变化敏感, 即应力变化一点点, 可以有明显的塑性应变变化, 相反, 塑性应变变化一点, 应力几乎不变化, 这对以后研究PBX材料的破坏准则具有非常重要的意义。
|
图 4 应力与塑性应变关系线性的Drucker-Prager模型模拟结果与实验结果对比 Fig.4 Comparison of liner Drucker-Prager model numerical and experimental results |
边界条件:面1573和面2684不受约束, 面1342面3784固定以控制刚体位移, 面5786、面1562受到与其法向方向相同的压缩强制位移, 位移量为0.02 mm。加载控制方式为位移线性加载。
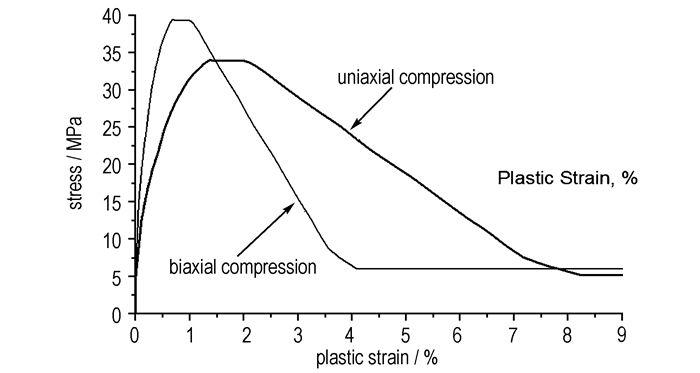
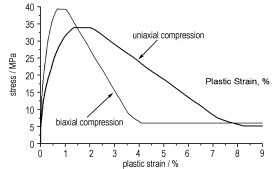
为了便于比较, 提取模拟结果中Y方向的应力与塑性应变, 取正, 并与单轴压缩状态的模拟结果对照, 如图 5所示。可以看出, 双轴压缩下PBX材料的极限强度比单轴压缩下高, 但是所能承受的应变反而小。具体分析, 提取模拟结果数据可得出, 双轴压缩下的极限强度为39.45 MPa, 此时对应塑性应变为0.69%, 双轴压缩下的极限强度与单轴压缩之比为1.16, 相对应的塑性应变之比为0.5, 这与式(48)、(50)理论分析结果一致。这验证了基于线性Drucker-Prager模型的弹塑性分析原理与Abaqus中线性Drucker-Prager模型是一致的。这表明线性Drucker-Prager模型能够描述双轴压缩比单轴压缩极限强度略高的现象。由于材料配方的特殊性及实验条件的局限性, 尚缺乏该PBX双轴压缩的实验数据。
|
图 5 双轴压缩与单轴压缩数值模拟结果比较 Fig.5 Comparison of numerical simulation results for biaxial and uniaxial compression |
(1) 根据PBX材料的力学行为及其影响因素, 基于线性Drucker-Prager模型, 考虑了PBX材料承载过程中存在的剪胀效应, 采用非相关流动势, 分析了弹性与塑性准静态加载中的变形过程, 推导出了PBX材料弹塑性本构模型, 并给出了塑性泊松比及等效应变系数的求解方法。本构模型中许多参数与温度、应变率相关, 为进一步研究温度、应变率等对PBX材料变形的影响提供了选择。
(2) 以单轴压缩、双轴压缩状况为算例, 根据文献[13]中的参数及塑性硬化数据, 进行了理论分析与数值模拟。理论分析结果显示, 在参数确定下, 单轴压缩下的应力应变关系取决于塑性硬化数据, 数值模拟结果上应力应变曲线与塑性硬化数据吻合的非常好, 这证明了线性Drucker-Prager模型在PBX材料变形研究中的适用性。根据双轴压缩模拟结果与单轴压缩模拟结果的比较, 验证了弹塑性理论分析与数值模拟结果是一致的。线性Drucker-Prager模型对PBX材料的适用, 则为进一步研究PBX材料在拉压共存等复杂应力状态下的力学行为提高了选择。
| [1] |
罗景润. PBX的损伤、断裂及本构关系研究[D]. 绵阳: 中国工程物理研究院, 2001.
LUO Jing-run. Damage, fracture and constitutive relation of PBX[D]. Mianyang: China Academy of Engineering Physics, 2001. http://cdmd.cnki.com.cn/Article/CDMD-82818-2001004174.htm |
| [2] |
郭虎. 高聚物粘结炸药微裂纹统计本构模型研究[D]. 绵阳: 中国工程物理研究院, 2012.
GUO Hu. Microcracks statistical constitutive model of polymer bonded explosive[D]. Mianyang: China Academy of Engineering Physics, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2906946 |
| [3] |
陈鹏万, 黄风雷.
含能材料损伤理论及应用[M]. 北京: 北京理工大学出版社, 2006: 6-17.
CHEN Peng-wan, Huang Feng-lei. Energetic Material Damage Theory and Applications[M]. Beijing: Beijing Institute of Technology Press, 2006: 6-17. |
| [4] |
Belmas R and Reynier P. Mechanical behavior of pressed explosives[C]//In: International Symposium Energetic Materials Technology Florida, March 21-23, 1994: 360-365.
|
| [5] |
Ellis K, Leppard C, Radesk H. Mechanical properties and damage evaluation of a UK PBX[J].
Journal of Materials Science, 2005, 40: 6241-6248. DOI:10.1007/s10853-005-3148-4 |
| [6] |
Wiegand D A, Reddingius B. Mechanical properties of confined explosives[J].
Energetic Materials, 2005, 23: 75-98. DOI:10.1080/07370650590936415 |
| [7] |
Blaine Asay.
Shock Wave Science and Technology Reference Library, Vol. 5. Non-Shock Initiation of Explosives[M]. Springer-Verlag, Berlin: 2010: 223-267.
|
| [8] |
温茂萍, 李明, 庞海燕, 等. 炸药件力学性能各向同异性试验研究[J].
含能材料, 2006, 14(4): 286-289. WEN Mao-ping, LI Ming, PANG Hai-yan, et al. Test study on explosive's isotropic and anisotropic of mechanical properties[J]. Chinese Journal of Energetic Materials(Hanneng Cailliao), 2006, 14(4): 286-289. |
| [9] |
Qin J, Lin Y, Lu F, et al. Dynamic compressive properties of a PBX analog as a function of temperature and strain rate[C]//Conference Proceeding of the Society for Experimental Mechanics Series 99, Kunming, 2011: 141-146.
|
| [10] |
陈刚, 黄西成, 张青平, 等. 一种PBX炸药的损伤模型参数[C]//第九届全国爆炸力学学术会议, 西宁, 2012: 176-180.
CHEN Gang, HUANG Xi-cheng, ZHANG Qing-ping, et al. The damage model parameters of the PBX[C]//Ninth National Explosion Conference, Xining, 2012: 176-180. |
| [11] |
YAN Qing-wu, FENG Lei-huang. A micromechanical model for predicting combined damage of particles and interface debonding in PBX explosives[J].
Mechanics of Materials, 2009, 41: 27-47. DOI:10.1016/j.mechmat.2008.07.005 |
| [12] |
郭虎, 罗景润. 基于微裂纹统计模型的PBX力学行为[J].
火炸药学报, 2012, 35(5): 52-56. GUO Hu, LUO Jing-run. The mechanical behavior of PBX based on micro-cracks statistical model[J]. Chinese Journal of Explosives, 2012, 35(5): 52-56. |
| [13] |
Gruau C, Picart D, Belmas R. Ignition of a confined high explosive under low velocity impact[J].
International Journal of Impact Engineering, 2009, 36: 537-550. DOI:10.1016/j.ijimpeng.2008.08.002 |
| [14] |
Yu T, Teng J G, Wong Y L, et al. Finite element modeling of confined concrete-Ⅰ: Drucker-Prager type plasticity model[J].
Engineering Structures, 2010, 32: 665-679. DOI:10.1016/j.engstruct.2009.11.014 |
| [15] |
袁小平, 刘红岩, 王志乔. 基于Drucker-Prager准则的岩石弹塑性损伤本构模型研究[J].
岩土力学, 2012, 33: 1103-1108. YUAN Xiao-ping, LIU Hong-yan, WANG Zhi-qiao. Elastoplastic damage constitutive model of rock based on Drucker-Prager criterion[J]. Rock and Soil Mechanics, 2012, 33: 1103-1108. DOI:10.3969/j.issn.1000-7598.2012.04.021 |
| [16] |
张艳山, 潘玉珍. 基于ABAQUS对Drucker-Prager系列准则的讨论[J].
水电能源科学, 2010, 28: 70-71. ZHANG Yan-shan, PAN Yu-zhen. Discussion about the Drucker-Prager criterion series by ABAQUS[J]. Water Resources and Power, 2010, 28: 70-71. |
| [17] |
刘金龙, 栾茂田, 许成顺, 等. Drucker-Prager准则参数特性分析[J].
岩石力学与工程学报, 2006, 25: 4009-4015. LIU Jin-long, LUAN Mao-tian, XU Cheng-shun, et al. Drucker-Prager criterion parameter characterization[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25: 4009-4015. DOI:10.3321/j.issn:1000-6915.2006.z2.106 |
| [18] |
王金昌, 陈叶开.
ABAQUS在土木工程中的应用[M]. 杭州: 浙江大学出版社, 2006: 22-23.
WANG Jin-chang, CHEN Ye-kai. ABAQUS application in Civil Engineering[M]. Hangzhou: Zhejiang University Press, 2006: 22-23. |
| [19] |
陈惠发, AF萨里普.
弹性与塑性力学[M]. 北京: 中国建筑工业出版社, 2004: 99-102.
CHEN Hui-fat, A F S. Elastic and plastic mechanics[M]. Beijing: China Architecture & Building Press, 2004: 99-102. |
Based on the linear Drucker-Prager model, combined with the classical plasticity theory, the quasi static elastic-plastic deformation process of the PBX was analyzed. The unit characteristics of PBX material were simulated by the linear Drucker-Prager model.




