2. 炮兵学院南京分院, 江苏 南京 211132
2. Nanjing Branch, Artillery Institute Nanjing, Nanjing 211132, China
点传火技术是火炮射击过程中的关键技术之一, 点传火系统的好坏直接影响到火炮的内弹道性能[1-3]。一般的大口径长药室火炮, 按装药结构来区分点传火形式, 通常粒状药采用中心传火管点火, 管状药采用底部点火。但是, 对于大口径平衡炮而言, 内部装药量大, 为改善传火通道一般采用管状装药。传统的底部点火, 传火时间长, 压力波动大, 是不安全的[4]。近年来, 国内外相继提出了许多新型的点火概念, 如激光点火[5-6]、新型电点火、等离子点火、网络点火等, 这些新型点火技术理论上都能够降低或避免大口径火炮普遍存在的点火延迟和局部点火现象, 但实际应用中电能的加载、时序放电的控制和火药气体的状态平衡方面仍存在许多技术困难[7-10]。为此, 轴向中心点火系统的改进和多点点火系统仍然是解决包括平衡炮在内的新型高性能大口径火炮点火问题的研究方向。
文献[11]中设计了多点点火装置, 但是仅对多点点火的发火一致性进行了试验研究, 并未对多点点火系统的内弹道性能进行相关的理论研究。本工作基于文献[11]的研究, 采用内弹道两相流理论, 对不同点火头数目、相同规格传火管内的点传火过程进行了数值模拟, 并结合在相应点传火模拟试验装置中的试验结果, 对比分析了燃气流动和能量释放过程, 得到了点火数量及点火位置在控制压力波强度, 抑制反常膛压等方面的规律, 为提升大口径长药室平衡炮内多点点传火结构设计提供了参考。
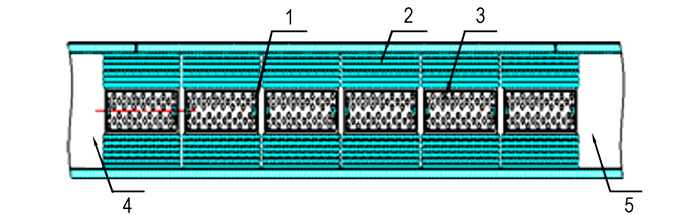
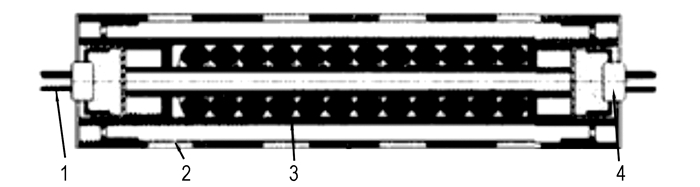
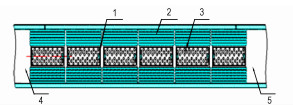
2 多点点火结构及模拟试验装置本研究所用的某大口径平衡炮装药及点传火系统如图 1所示。多点点火系统由6节传火管前后紧密衔接而成。单节传火管长0.5 m, 其中两端两节长0.51 m, 采用内管、外管套装结构, 见图 2。内管起点火作用, 外管起传火功能, 且内外管管体均可燃。点火具内外管均采用可燃药筒制成, 外管表面预制传火孔, 内管两端为装有小粒黑的点火药盒, 中间装填装大粒黑火药的点火药包(蛇形药袋), 点火药盒通电发火后, 产生的火焰点燃点火药包(蛇形药袋)中黑火药, 黑火药燃烧产生的高温、高压气体将内管涨裂, 进而将能量通过外管表面传火孔传输到发射药表面, 点燃发射药。
|
图 1 火炮装药结构示意图 1—点火药盒, 2—发射药, 3—中心传火管, 4—弹丸, 5—平衡体 Fig.1 Schematic diagram of the charge of the gun 1—ignition box, 2—propellant, 3—center igniter tube, 4—projectile, 5—the counterpoise |
|
图 2 单节中心传火管结构示意图 1—点火导线, 2—喷孔, 3—蛇形药袋, 4—点火药盒及点火头 Fig.2 Schematic diagram of the single center igniter tube construction 1—ignition wire, 2—nozzle hole, 3—snake-shaped powder bag, 4—ignition box and igniter |
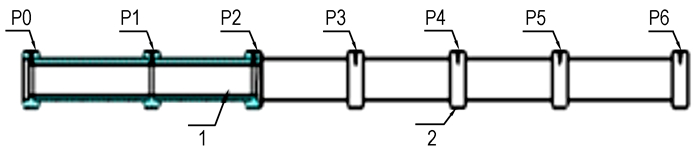
为研究其点传火性能, 设计了多点点火模拟装置, 如图 3所示[11]。节与节之间有衔接器, 可方便进行不同长度的试验, 每个衔接器上开有测压孔, 用于安装压力传感器。两端的衔接器设计有密封环, 用于压紧铝制膜片, 接线一端的铝制膜片上装有接线柱。试验采用的多点点传火系统共有12个点火源, 7个点火位置, 从左至右依次标记为P0-P6, 结构示意图如图 4所示。试验装置图如图 5所示。

|
图 3 多点点传火试验模拟装置结构示意图 1, 4—测压孔, 2, 3, 8—点火药盒, 5—泄压膜片, 6—中心传火管, 7—联接器 Fig.3 Schematic diagram of the multi-point ignition/flame spreading analog device 1, 4—piezometric holes, 2, 3, 8—ignition boxes, 5—relief diaphragm, 6—center igniter tube, 7—coupling |
|
图 4 点火头位置示意图 1—中心传火管, 2—联接器 Fig.4 Diagram of the position of the igniters 1—center igniter tube, 2—coupling |

|
图 5 多点点传火试验模拟装置照片 Fig.5 Photo of the multi-point ignition/flame spreading analog device |
对实际过程进行简化处理, 提出以下基本假设:
(1) 双流体假设。把大粒黑火药颗粒群当作一种具有连续介质特性的拟流体来处理, 认为大粒黑火药颗粒群组成的固相连续分布在气相中;
(2) 考虑火药颗粒和火药燃气的两相流动, 忽略径向流动的影响, 认为传火孔只喷出火药气体, 而无火药颗粒, 并且简化为轴向一维流动, 认为传火管的横截面面积不变;
(3) 假设黑火药的燃烧产物全为气相, 用比热比修正燃气混合物的热力学参量;
(4) 黑火药的着火准则为表面温度准则, 即火药表面温度达到着火温度火药开始燃烧;
(5) 假设黑火药的燃烧速度仅与压力相关, 忽略侵蚀燃烧和黑火药初始温度的影响;
(6) 忽略气体的粘性耗散和对管壁的热损失;
(7) 黑火药固体不可压缩, 黑火药固体颗粒大小一致, 用药粒的当量尺寸来表示全部药粒的尺寸;
(8) 黑火药燃气服从诺贝尔-阿贝尔状态方程;
(9) 对于相间阻力、颗粒间应力、相间热交换及化学反应等微观过程, 假定作为两相当地平均状态的函数, 并用经验方程处理。
3.2 守恒方程组基于以上假设, 结合文献[12], 建立数学模型如下:
(1)连续方程
气相连续方程:
| $ \frac{{\partial \left( {\mathit{\varphi }{{\mathit{\hat \rho }}_{\mathit{g}}}} \right)}}{{\partial \mathit{t}}}{\rm{ + }}\frac{{\partial \left( {\mathit{\varphi }{{\mathit{\hat \rho }}_{\rm{g}}}{\mathit{u}_{\rm{g}}}} \right)}}{{\partial \mathit{x}}}{\rm{ = }}{{\mathit{\dot m}}_{\rm{I}}}{\rm{ + }}{{\mathit{\dot m}}_{\rm{c}}}{\rm{ - }}{{\mathit{\dot m}}_{\rm{g}}} $ | (1) |
固相连续方程:
| $ \frac{{\partial \left[{\left( {{\rm{1-}}\mathit{\varphi }} \right){{\mathit{\hat \rho }}_{\rm{P}}}} \right]}}{{\partial \mathit{t}}}{\rm{ + }}\frac{{\partial \left[{\left( {{\rm{1-}}\mathit{\varphi }} \right){{\mathit{\hat \rho }}_{\rm{P}}}{\mathit{u}_{\rm{P}}}} \right]}}{{\partial \mathit{x}}}{\rm{ = - }}{{\mathit{\dot m}}_{\rm{c}}}{\rm{ - }}{{\mathit{\dot m}}_{\rm{P}}} $ | (2) |
φ为气相空隙率; ρg为气相物质密度, kg·m-3; ug为气相速度, m·s-1;
(2) 动量方程
气相动量方程:
| $ \frac{\partial }{{\partial \mathit{t}}}\left( {\mathit{\varphi }{{\mathit{\hat \rho }}_{\rm{g}}}{\mathit{u}_{\rm{g}}}} \right){\rm{ + }}\frac{\partial }{{\partial \mathit{x}}}\left( {\mathit{\varphi }{{\mathit{\hat \rho }}_{\rm{g}}}\mathit{u}_{\rm{g}}^2} \right){\rm{ + }}\mathit{\varphi }\frac{{\partial \mathit{p}}}{{\partial \mathit{x}}}{\rm{ = - }}{\mathit{f}_{\rm{s}}}{\rm{ + }}{{\mathit{\dot m}}_{\rm{I}}}{\mathit{u}_{\rm{I}}}{\rm{ + }}{{\mathit{\dot m}}_{\rm{c}}}{\mathit{u}_{\rm{p}}}{\rm{ - }}{{\mathit{\dot m}}_{\rm{g}}}{\mathit{u}_{\rm{g}}} $ | (3) |
固相动量方程:
| $ \frac{\partial }{{\partial \mathit{t}}}\left[{\left( {{\rm{1-}}\mathit{\varphi }} \right){{\mathit{\hat \rho }}_{\rm{p}}}{\mathit{u}_{\rm{p}}}} \right]{\rm{ + }}\frac{\partial }{{\partial \mathit{x}}}\left[{\left( {{\rm{1-}}\mathit{\varphi }} \right){{\mathit{\hat \rho }}_{\rm{p}}}\mathit{u}_{\rm{p}}^2} \right]{\rm{ + }}\left( {{\rm{1 - }}\mathit{\varphi }} \right)\frac{{\partial \mathit{p}}}{{\partial \mathit{x}}}{\rm{ + }}\\ \frac{\partial }{{\partial \mathit{x}}}\left[{\left( {{\rm{1-}}\mathit{\varphi }} \right){\mathit{R}_{\rm{p}}}} \right]{\rm{ = }}{\mathit{f}_{\rm{s}}} - {{\mathit{\dot m}}_{\rm{c}}}{\mathit{u}_{\rm{p}}}{\rm{ - }}{{\mathit{\dot m}}_{\rm{p}}}{\mathit{u}_{\rm{p}}} $ | (4) |
式中, fs, Rp表示相间阻力和颗粒间应力, N; uI为点火头内燃烧喷射进入黑火药时的气体速度, m·s-1; uP为黑火药气体从传火孔流出的速度, m·s-1。
(3) 气相能量方程
| $ \begin{array}{l} \frac{\partial }{{\partial \mathit{t}}}\left[{\mathit{\varphi }{{\mathit{\hat \rho }}_{\rm{g}}}\left( {{\mathit{e}_{\rm{g}}}{\rm{ + }}\frac{{\mathit{u}_{\rm{g}}^2}}{2}} \right)} \right]{\rm{ + }}\frac{\partial }{{\partial \mathit{x}}}\left[{\mathit{\varphi }{{\mathit{\hat \rho }}_{\rm{g}}}{\mathit{u}_{\rm{g}}}\left( {{\mathit{e}_{\rm{g}}}{\rm{ + }}\frac{\mathit{p}}{{{{\mathit{\hat \rho }}_{\rm{g}}}}}\frac{{\mathit{u}_{\rm{g}}^2}}{2}} \right)} \right] + \mathit{p}\frac{{\partial \mathit{\varphi }}}{{\partial \mathit{t}}}\\ = {\rm{ - }}{\mathit{Q}_{\rm{p}}}{\rm{ - }}{\mathit{f}_{\rm{s}}}{\mathit{u}_{\rm{p}}}{\rm{ + }}{{\mathit{\dot m}}_{\rm{I}}}\left( {{\mathit{e}_{\rm{I}}}{\rm{ + }}\frac{\mathit{p}}{{{{\mathit{\hat \rho }}_{\rm{I}}}}}\frac{{\mathit{u}_{\rm{I}}^2}}{2}} \right){\rm{ + }}{{\mathit{\dot m}}_{\rm{c}}}\left( {{\mathit{e}_{\rm{p}}}{\rm{ + }}\frac{\mathit{p}}{{{{\mathit{\hat \rho }}_{\rm{p}}}}}\frac{{\mathit{u}_{\rm{p}}^2}}{2}} \right){\rm{ - }}\\ {{\mathit{\dot m}}_{\rm{g}}}\left( {{\mathit{e}_{\rm{g}}}{\rm{ + }}\frac{\mathit{p}}{{{{\mathit{\hat \rho }}_{\rm{g}}}}}\frac{{\mathit{u}_{\rm{g}}^2}}{2}} \right){\rm{ - }}{{\mathit{\dot m}}_{\rm{p}}}\left( {{\mathit{e}_{\rm{p}}}{\rm{ + }}\frac{\mathit{p}}{{{{\mathit{\hat \rho }}_{\rm{p}}}}}\frac{{\mathit{u}_{\rm{p}}^2}}{2}} \right) \end{array} $ | (5) |
Qp为相间传热, J·m-3·s-1; q表示相间热传导, J·m-3·s-1; ep为固相比内能, J·kg-1; eg为气相比内能, J·kg-1; eI为点火头内火药燃烧释放出的化学能J·kg-1。
(4) 辅助方程
辅助方程包括相间阻力、相间热交换、状态方程、火药燃烧速率、形状函数、颗粒间应力和火药表面温度的方程, 具体参见文献[12]。
4 点传火特性对比分析对于长度3.2 m的药室采用单点底部点火或顶端点火, 势必会造成不均匀的局部点火, 容易产生火药床的挤压和药粒群在底部和端部的堆积现象, 讨论单点底部或端部点火是没有任何意义的。因此, 本研究讨论中间单点点火, 即P3点点火, 两点点火: P2, P4中间两点和P1, P5两端两点点火几种情况的点传火特性。采用Mac Cormack差分格式[12]对上节建立的模型进行数值模拟, 传火管尺寸、发射药量、底火加入的时间等量都保持不变, 点火药盒产生的火药气体以源项形式加入传火管方程, 通过控制源项加入的位置, 实现点火数量和点火位置的调整, 对得到的计算结果展开对比分析如下。
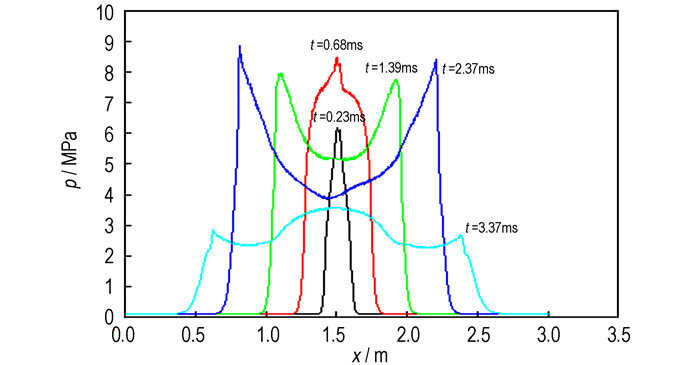
4.1 P3单点点火图 6和图 7为采用单点点火时传火管内的压力和空隙率计算曲线。由图 6单点点火时压力沿轴向分布图可以看出, 在点火初始由于点火药盒燃烧产生的高温高压火药气体的加入, 形成沿轴向的初始压力梯度。点火药盒产生的火药气体通过对流和辐射作用加热附近的大粒黑火药, 引燃更多的火药, 产生压力阵面的移动, 火药气体进而随着压力波向药盒两边传播。火药气体在通过点火间隙时流动遇到阻碍, 压力波使得未点燃的黑火药颗粒也由点火药盒向两边运动。
|
图 6 单点点火时压力沿轴向分布图 Fig.6 Pressure distribution along axis of the single point ignition |
|
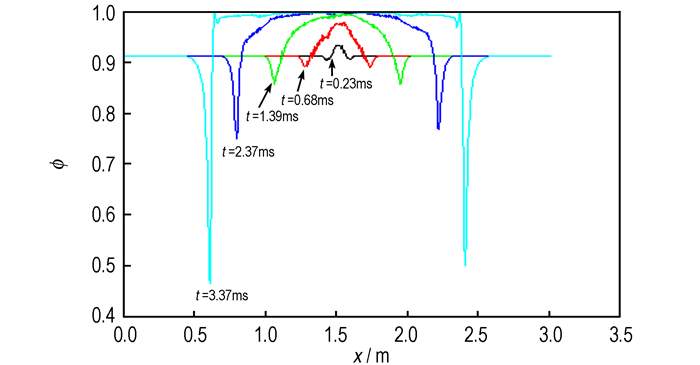
图 7 单点点火时空隙率沿轴向分布图 Fig.7 Void ratio distribution along axis of the single point ignition |
由图 7空隙率分布曲线可以看出, 在压力波的作用下, 未点燃的火药向中心管两端运动, 在运动的过程中即出现空隙率的大幅度降低, 且随着时间的推移, 出现较低的空隙率, 3.37 ms时火药仍未全面点燃, 离两端0.6 m左右处的火药空隙率已经降到了0.5以下, 说明火药颗粒在此处已经堆积较为严重。实际应用中, 由于点火药的刚性较差, 药粒运动堆积过程中的碰撞, 很可能导致药粒的破碎和变形, 传火通道被堵塞等, 造成点火管不同部位的异常压力输出, 进一步影响点火药的正常燃烧, 出现异常。因此, 这种大量堆积的现象对发射安全性无疑是不利的。
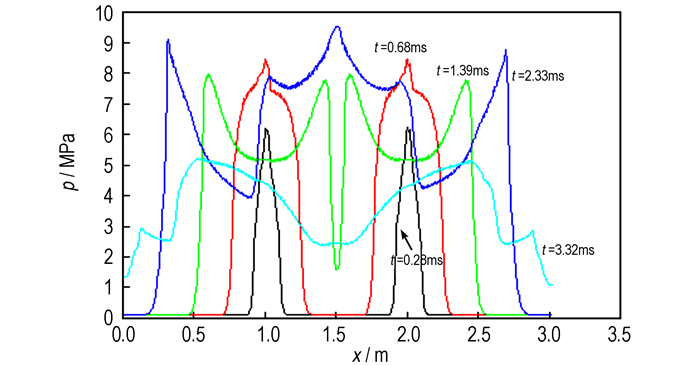
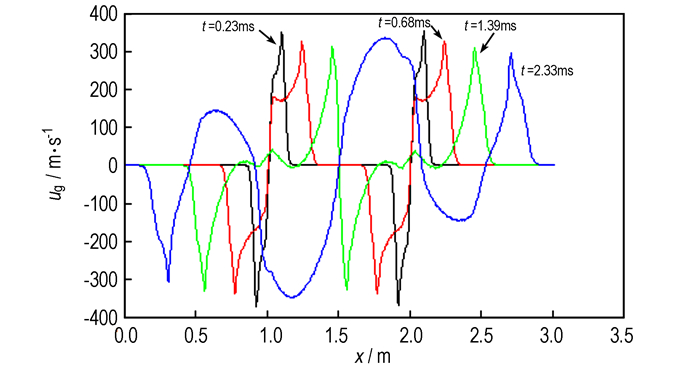
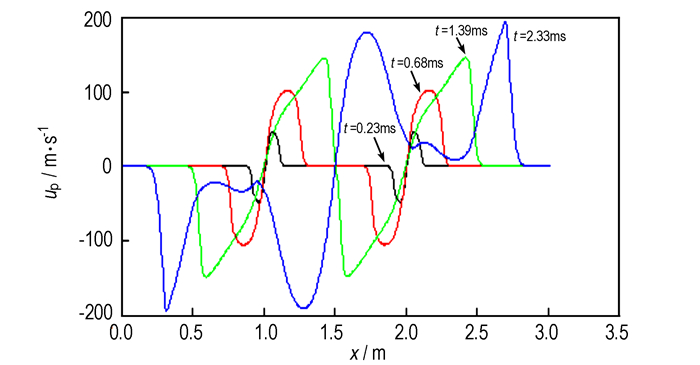
4.2 P2, P4中间两点点火由图 8中P2, P4中间两点点火的压力计算曲线可以看出, 由于点火发生在两点, 点火开始后, 压力波分别向两端和中间推进, 压力峰值随着压力波的移动而移动, 2.33 ms左右中间两波相遇时产生更高的压力峰值。从图 9和图 10中的速度分布曲线也可以看出, 由于气体和火药颗粒同时向两端和中间运动, 因此, 与单点点火相比, 火药气体传播的面积更广, 传火时间缩短。
|
图 8 P2, P4中间两点点火时压力沿轴向分布图 Fig.8 Pressure distribution along axis of the two-point ignition (P2 and P4 intermediate points) |
|
图 9 P2, P4中间两点点火时气相速度沿轴向分布图 Fig.9 Gas velocity distribution along axis of the two-point ignition(P2 and P4 intermediate points) |
|
图 10 P2, P4中间两点点火时固相速度沿轴向分布图 Fig.10 Gas velocity ratio distribution along axis of the two-point ignition(P2 and P4 intermediate points) |
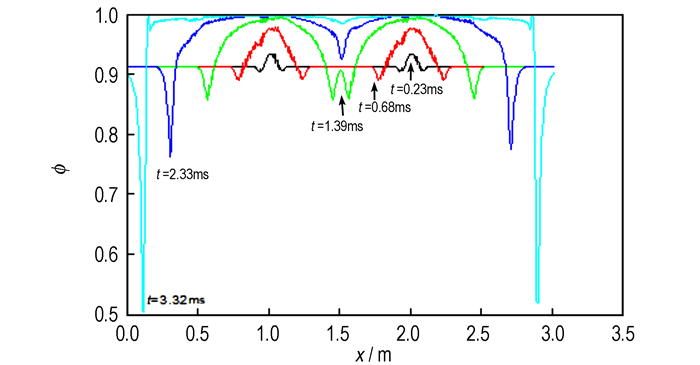
P2, P4中间两点点火时, 向两端传播距离大于往中间传播的距离, 但向两端传播距离小于单点点火方式, 图 11表明火药堆积的范围较单点点火缩小, 3.32 ms时空隙率在靠近两端处出现了较低的值, 说明堆积现象仍比较严重。
|
图 11 P2, P4中间两点点火时空隙率沿轴向分布图 Fig.11 Void ratio distribution along axis of the two-point ignition(P2 and P4 intermediate points) |
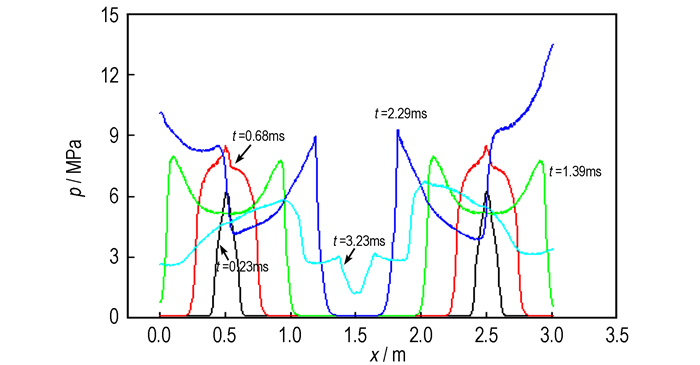
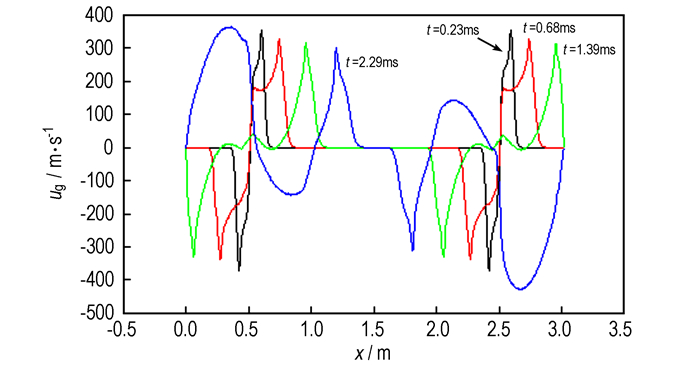
图 12~图 15为P2, P5两端点同时点火所得特征量曲线。同P2, P4中间两点点火一样, P1, P5两端两点点火的传火时间, 传火速度也明显优于单点点火。
|
图 12 P1, P5两端点点火时压力沿轴向分布图 Fig.12 Pressure distribution along axis of the two-point ignition (P1 and P5 end points) |
|
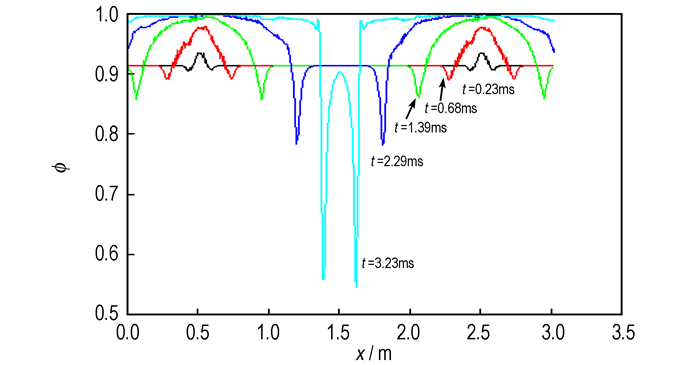
图 13 P1, P5两端点点火时空隙率沿轴向分布图 Fig.13 Void ratio distribution along axis of the two-point ignition(P1 and P5 end points) |
|
图 14 P1, P5两端点点火时气相速度沿轴向分布图 Fig.14 Gas velocity distribution along axis of the two-point ignition (P1 and P5 end points) |
|
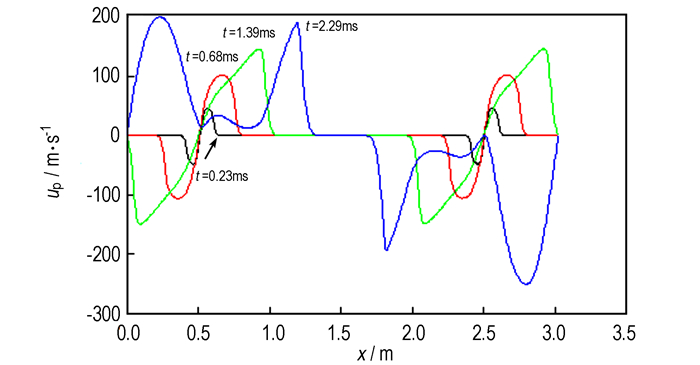
图 15 P1, P5两端点点火时固相速度沿轴向分布图 Fig.15 Gas velocity distribution along axis of the two-point ignition(P1 and P5 end points) |
与P2, P4中间两点点火不同的是, 此时, 压力波向中间传播的距离大于两端, 压力波达到中间的时间滞后, 火药在中间堆积明显, 3.23 ms时传火接近中间时出现了较低的空隙率。从以上对比不难得出结论, 压力梯度的不均匀分布, 压力波在传火管内传播的强度和时间, 是产生火药堆积的主要原因。
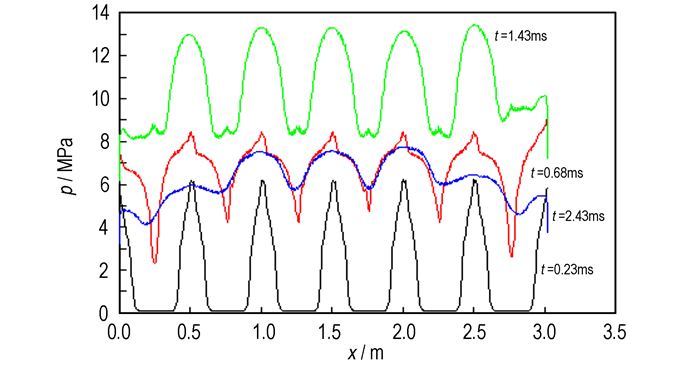
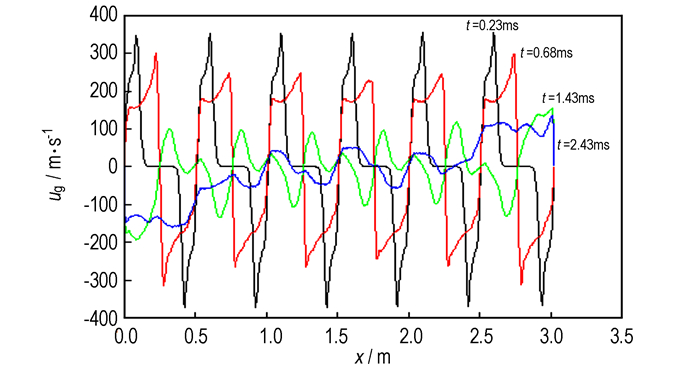
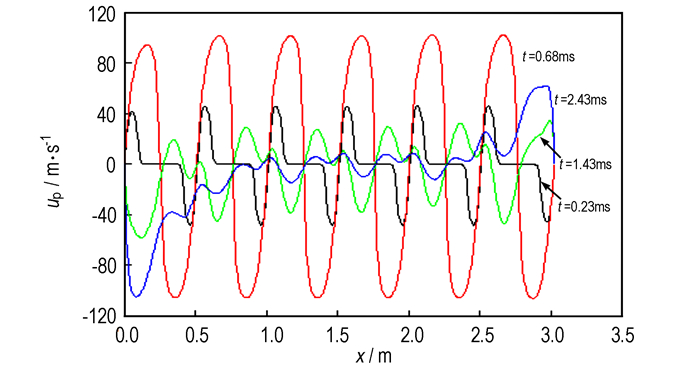
4.4 七点点火图 16为七点点火时压力沿轴向分布图, 由图中可见点火初始, 由于七个点火药盒同时产生火药气体向两边喷出, 因此形成锯齿状的压力梯度分布。七个点火头同时点火, 主装药被点燃的面积大, 短时间内中心管内整体压力迅速升高。图 17和图 18中速度曲线也可以看出, 气相和固相向两边流动的速度并没有因为压力的变化而加快, 反而随着时间的推移, 逐渐减缓, 说明点火管内压力波强度较小, 火药在点火药盒附近稳定燃烧, 直到两端膜片打开。整个过程压力分布均匀, 气体和颗粒流动不剧烈, 有助于形成均匀一致的点火, 降低初速散布。
|
图 16 七点点火时压力沿轴向分布图 Fig.16 Pressure distribution along axis of the seven-point ignition |
|
图 17 七点点火时气相速度沿轴向分布图 Fig.17 Gas velocity distribution along axis of the seven-point ignition |
|
图 18 七点点火时固相速度沿轴向分布图 Fig.18 Solid velocity distribution along axis of the seven-point ignition |
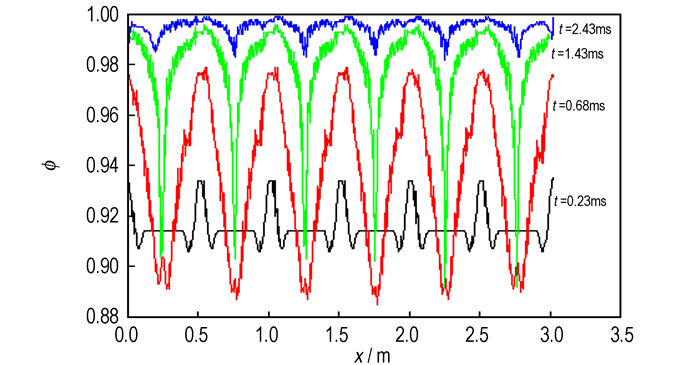
从图 19中可以看出, 空隙率在整个点传火过程中分布也较为稳定, 两个点火药盒之间的空隙率略微低于点火药盒处, 但都保持较高的值, 没有造成明显的火药堆积现象。说明采用多点点火技术大大提高了点传火的安全性。均匀的火药气体也对保证火药充分燃烧, 提高火药利用率有利。
|
图 19 七点点火时空隙率沿轴向分布图 Fig.19 Void ratio distribution along axis of the seven-point ignition |
此外, 还可以看出, 采用多点点火技术, 2.43 ms时点火管内的火药已经接近全部燃完, 火药气体充斥着整个点火管, 传火时间远远小于单点点火和两点点火。这说明改进的多点点火方案对减小传火距离相对较长的大口径长药室平衡炮传火时间有利。
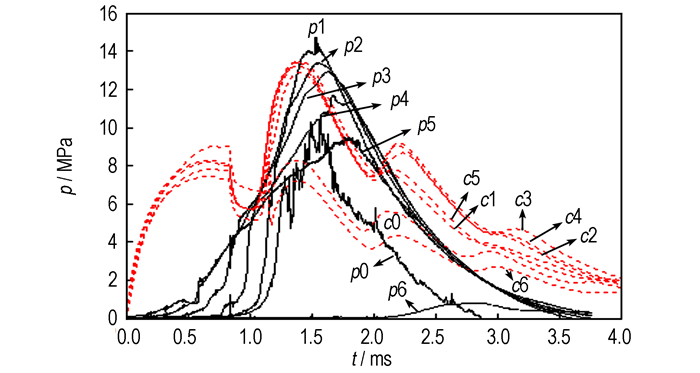
在数值分析的基础上, 在上面介绍的点传火模拟试验装置上进行了七点点传火试验。试验证明这12个点火源均工作正常, 由图 20可见, 达到最大压力的时间及趋势基本吻合, 未见明显的压力振荡, 说明点传火系统点传火性能良好, 结构设计合理。计算所得的点火头附近压力曲线和试验结果相对吻合。误差出现在点火开始阶段, 这是由于试验测压孔安装在点火管壁, 且点火头内的点火药逐渐燃烧流入传火管, 而计算过程更主要反映的是传火管中心形成的瞬时高压, 点火药以火药气体的形式从源项快速加入, 因此压力上升较快。计算结果和试验结果都表明, 采用多点点火技术传火管内各点压力一致性好, 有利于提高大口径长药室火炮点传火特性。但是, 对于一定长度的药室, 传火管的长度也是有限的, 太多的点火头数必然导致工艺难度增加, 连接更为复杂, 点火过程中的不稳定因素增多, 因此在应用多点点火技术的同时, 要适当控制点火头数。本研究的某大口径平衡炮内采用七点点火可行性高, 满足了设计要求。
|
图 20 七点点火各测压点处压力曲线试验与计算结果对比图 p0~p6—测压点P0-P6测得曲线, c0~c6—点火头处计算曲线 Fig.20 Comparison chart of calculated and experimental pressure in the seven-point ignition p0~p6—pressure curve tested by pressure sensor at igniters senser P0-P6, c0~c6: calculation curves on the igniters position at P0-P6 |
针对大口径长药室平衡炮炮内点传火距离长, 药量大等问题, 建立了某中心点传火装置的一维两相流模型, 并对几种点火头数量下的相同传火管的点传火过程进行数值模拟, 得到分别采用单点点火、两点(中间和两端)点火及七点点火三种方式的传火管内压力、两相速度、空隙率分布规律, 并与相关试验结果进行对比, 分析表明:
(1) 对大口径长药室平衡炮而言, 采用单点点火结构传火时间长, 容易造成火药在局部大量堆积, 不利于发射安全性。
(2) 采用两点点火结构(3.3 ms), 较单点点火(3.37 ms)可以缩短传火时间, 但是在改善火药堆积问题上仍有欠缺。
(3) 采用多点点火结构可以有效缩短传火时间(2.43 ms), 提高点火压力均匀性和一致性, 有利于保证火药正常燃烧, 从而避免传火管内压力波异常现象的发生。试验结果也进一步证实了计算分析的合理性。多点点火技术在大口径长药室平衡炮中应用具有优越性。但是要注意的是, 点火头数过多会加大实际操作上的难度, 因此要根据实际情况合理增加点火头数目。
| [1] |
焦旭英, 张玉成, 杜江媛, 等. 一种提高点传火系统安全性的方法[J].
兵工自动化, 2013, 32(1): 46-47. JIAO Xu-ying, ZHANG Yu-cheng, DU Jiang-yuan, et al. One way to improve safety of ignition and flame spreading system[J]. Ordnance Industry Automation, 2013, 32(1): 46-47. DOI:10.7690/bgzdh.2013.01.014 |
| [2] |
East J L, Burrell W R. Solutions to ignition related problems in navy guns via a rapid ignition propagation (RIP) ignition[C]//14th JANNAF Combustion Meeting CPIA, Publication, 1977: 292.
|
| [3] |
王珊珊, 张玉成, 王浩, 等. 大长径比点火管高密实火药床点传火过程两相流的数值模拟[J].
爆炸与冲击, 2013, 33(4): 444-447. WANG Shan-shan, ZHANG Yu-cheng, WANG hao, et al. Two-phase flow in ignition process of consolidated charge bed within a large length-to-diameter ratio igniter tube[J]. Explosion and Shcok Waves, 2013, 33(4): 444-447. |
| [4] |
徐流恩, 李永池, 高乐南. 大口径高速平衡炮发射安全性分析[J].
中国科学技术大学学报, 2008, 38(11): 1304-1309. XU Liu-en, LI Yong-chi, GAO Le-nan. Shooting security analysis of counter-mass propelling gun with large caliber and high muzzle velocity[J]. Journal of University of Science And Technology of China, 2008, 38(11): 1304-1309. |
| [5] |
李海庆, 张小兵, 李筱伟, 等. 激光多点点火二维两相流数值模拟[J].
兵工学报, 2012, 33(3): 257-260. LI Hai-qing, ZHANG Xiao-bing, LI Xiao-wei, et al. Two-dimensional two-phase flow numerical simulation of multi-point laser ignition[J]. Acta Armamentarii, 2012, 33(3): 257-260. |
| [6] |
王殿湘, 尹国福, 贺爱锋, 等. 激光多点点火系统自诊断检测技术研究[J].
火工品, 2013(6): 51-53. WANG Dian-xiang, YIN Guo-fu, HE Ai-feng, et al. Study on build-in test technology for laser multi-point initiation system[J]. Initiators & Pyrotechnics, 2013(6): 51-53. |
| [7] |
黄明, 王浩. 传火管中不同装药结构传火性能试验研究[J].
弹道学报, 2003, 15(1): 83-86. HUANG Ming, WANG Hao. The experimental study on the pefomance of ignition and flame spreading in igniter for different charge constructions[J]. Journal of Ballistics, 2003, 15(1): 83-86. |
| [8] |
Brad E. Trends observed in the laser ignition of black powder and JA2 propellant. ADA277904[R], 1994
|
| [9] |
王浩, 黄明, 邵志坚. 火炮中激光多点点火技术试验研究[J].
兵工学报, 2000, 21(2): 101-104. WANG Hao, HUANG Ming, SHAO Zhi-jian. A study on the laser multi-point ignition of guns[J]. Acta Armamentarii, 2000, 21(2): 101-104. |
| [10] |
狄加伟, 杨敏涛, 张明安, 等. 电热化学发射技术在大口径火炮上的应用前景[J].
火炮发射与控制学报, 2010(2): 24-27. DI Jia-wei, YANG Min-tao, ZHANG Ming-an, et al. Electrothermal-chemical launcher technology in large caliber gun[J]. Journal of Gun Launch and Control, 2010(2): 24-27. |
| [11] |
季晓松, 王浩, 冯国增, 等. 高炮口动能大口径火炮中多点点火技术试验研究[J].
弹道学报, 2010, 22(4): 67-69. JI Xiao-song, WANG Hao, FENG Guo-zeng, et al. Experimental research on technology of multi-point ignition in large caliber gun with high muzzle energy[J]. Journal of Ballistic, 2010, 22(4): 67-69. |
| [12] |
翁春生, 王浩.
计算内弹道学[M]. 北京: 国防工业出版社, 2006.
WONG Chun-sheng, WANG Hao. Computational interior ballistics[M]. Beijing: National defense Press, 2006. |
Based on the test results of multi-point ignition in large caliber balance gun, combined with the numerical simulation of the single-point ignition, the two-point ignition and the multi-point ignition, the ignition characteristics and rules of the multi-point technology were researched.



