2. 中国工程物理研究院安全弹药研发中心, 四川 绵阳 621999;
3. 中物院高性能数值模拟软件中心, 北京 100080;
4. 北京应用物理与计算数学研究所, 北京 100080
2. Robust Munitions Center, CAEP, Mianyang 621999, China;
3. Software Center for High Performance Numerical Simulation, Beijing 100080, China;
4. Institute of Applied Physics and Computational Mathematics, Beijing 100080, China
在储存、运输和使用过程中, 弹药有遭受意外火灾, 发生燃烧、爆炸甚至殉爆的风险, 因此合理评估炸药热安全性非常重要。目前对弹药的热安全性研究主要是烤燃试验和数值模拟, 烤燃试验是针对装药的宏观响应特性进行直接观测, 数值模拟则针对炸药热分解过程进行综合分析, 具有成本低、周期短、数据全面等优点, 与烤燃试验相辅相成, 是目前研究的热点。
20世纪90年代中期, 烤燃数值模拟主要是编译程序, 对炸药点火特征信息进行计算。Jones[1]基于Fortran语言开发了HEAT软件, 对烤燃过程中的炸药温度分布进行了研究。而90年代末至今, 相关专业软件的发展为烤燃过程的研究提供了更好的平台, Howard[2], McClelland[3]等利用ALE3D软件对多种炸药烤燃试验过程中的反应动力学进行了研究。国内专家学者也对炸药烤燃试验做了大量的研究工作。由于国外专业软件的禁运, 我国的研究工作主要是借助现行商业软件。王沛[4], 陈朗[5]张晓立[6]陈科全[7]等人分别利用FLUENT、LS-DYNA3D、ABAQUS软件对烤燃试验全过程进行了分析。限于商业软件的功能, 这些研究并未针对炸药的反应动力学进行细致表征。
为此, 本课题组自主编写了“含能材料动态响应数值模拟软件”(Dynamic Response Simulation package for Energetic Materials), 并使用该软件中的反应动力学模块, 针对黑索今(RDX)基高聚物粘结炸药(PBX)的烤燃过程, 进行了数值模拟, 研究其在不同升温率下相关组分的变化规律。
2 计算方法及模型校验 2.1 计算方法在加热过程中, 热量以热传导形式通过壳体向炸药内部传递, 受热后, 炸药会发生复杂的多步热分解反应, 先将热能转化为化学能, 再将化学能转化为热能释放出来, 随着热量的积累, 反应速率会逐渐加快, 最终导致炸药点火。
对于以RDX为基的PBX炸药, 其受热分解过程可用(1)式、(2)和(3)式[8], 相关物理化学参数见表 1。
| 表 1 炸药和壳体的物性参数及反应动力学参数[8-9] Tab.1 Physical parameters and chemical kinetic parameters for RDX-based PBX and steel |
| $ A \to B\;\;\;{r_1} = {Z_1}\exp \left( {- {E_1}/RT} \right)\left[A \right] $ | (1) |
| $ B \to C\;\;\;{r_2} = {Z_2}\exp \left( {- {E_2}/RT} \right)\left[B \right] $ | (2) |
| $ C \to \mathit{D}\;\;\;{r_3} = {Z_3}\exp \left( {- {E_3}/RT} \right){\left[C \right]^2} $ | (3) |
式中,r为反应速率, mol·L-1·s-1; Z为指前因子, s-1; E为活化能, J·mol-1; m为反应序号, m=1, 2, 3; R为普适气体常数, 8.314 J·mol-1·K-1; A为RDX炸药; B为固体中间产物; C为气体中间产物; D为气体终产物; [A], [B], [C], [D]分别为其对应的质量分数, kg·m-3。反应(1)是固体吸热一级化学反应, 反应(2)是固体中间产物向气体中间产物转变的放热一级化学反应, 反应(3)是气体中间产物分解为气体终产物的强放热二级化学反应, 也是炸药点火的主导反应。
因此其动力学方程可表示为:
| $ \frac{{{\rm{d}}\left[A \right]}}{{{\rm{d}}\mathit{t}}} = - {Z_1}\exp \left( { - {E_1}/RT} \right)\left[A \right] $ | (4) |
| $ \frac{{{\rm{d}}\left[B \right]}}{{{\rm{d}}\mathit{t}}} = - {Z_1}\exp \left( { - {E_1}/RT} \right)\left[A \right] - {Z_2}\exp \left( { - {E_2}/RT} \right)\left[B \right] $ | (5) |
| $ \frac{{{\rm{d}}\left[\mathit{C} \right]}}{{{\rm{d}}\mathit{t}}} = {Z_2}\exp \left( { - {E_2}/RT} \right)\left[B \right] - {Z_3}\exp \left( { - {E_3}/RT} \right)\left[C \right] $ | (6) |
| $ \frac{{{\rm{d}}\left[\mathit{D} \right]}}{{{\rm{d}}\mathit{t}}} = {Z_4}\exp \left( { - {E_4}/RT} \right){\left[C \right]^2} $ | (7) |
在二维柱坐标系中, 热量传递方程的形式为[10]:
| $ \rho c\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {\lambda r\frac{{\partial T}}{{\partial r}}} \right) + \frac{\partial }{{\partial Z}}\left( {\lambda \frac{{\partial T}}{{\partial r}}} \right) + S $ | (8) |
| $ \begin{array}{l} S = {Q_1}{Z_1}\exp \left( {- {E_1}/RT} \right)\left[A \right] + {Q_2}{Z_2}\exp \left( { - {E_2}/RT} \right)\left[B \right] + \\ \;\;\;\;\;\;{Q_3}{Z_3}\exp \left( { - {E_3}/RT} \right){\left[C \right]^2} \end{array} $ | (9) |
| $ T\left( {r, z, t} \right) = {T_s} $ | (10) |
式中, ρ是密度, kg·m-3; c是比热, J·kg-1·K-1; T是温度, K; λ是热导率, W·m-1·K-1; S为炸药自热反应源项, Q为反应的反应热。方程(10)表示第一类边界条件, 其意义是在边界上给定温度值。
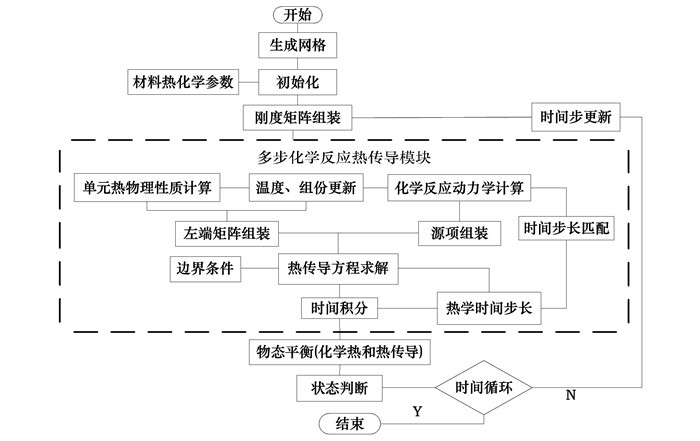
2.2 计算流程计算流程如图 1所示, 主要包括多步化学反应动力学计算和和热传导两部分。多步化学反应动力学部分包括计算化学组份变化及热源项, 其难点是: (1)化学反应动力学计算与宏观的烤燃过程存在较强的时间多尺度问题, 并且化学反应控制方程也存在较强的刚性。为了削弱这些问题, 程序根据温度梯度来自适应调节子程序中的时间步长, 当温度梯度超过一定限制时将时间步长缩减为原来的1/10。(2)化学反应初期反应物消耗较低导致数值计算存在误差问题, 程序以产物的生成量作为反应进度的标准以减小数值误差。
|
图 1 计算流程图 Fig.1 Sketch diagram of calculation method |
热传导部分主要是利用有限元的基本思想进行计算, 包括建立左端矩阵、源项, 以及边界条件加载。对于时间积分部分, 主要是考虑到在烤燃前期温度变化缓慢, 故采用隐式方法进行时间离散, 取较大的时间步长进行计算; 在烤燃后期, 由于温度急剧升高, 计算中所取时间步长必须足够小, 故采用显式算法进行时间离散。显式算法和隐式算法之间的耦合切换通过温度变化率调整设定。
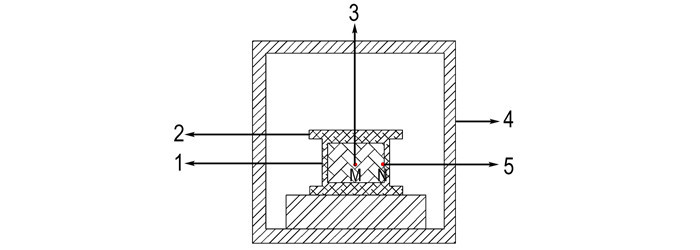
2.3 模型校验采用文献[9]中的试验结果校验本文计算方法。试验装置由加热烘箱、壳体、药柱、热电偶等组成[9], 如图 2所示。初始温度为300 K, 在升温速率为1 K·min-1, 壳体厚度为3 mm, 药柱尺寸为Φ40 mm×50 mm的条件下测量药柱中心(M点)和壳体外壁(N点)温度, 直至装药结构点火, 并记录点火时间于表 2中。
|
图 2 加热烘箱和烤燃试件[9] 1—炸药, 2—壳体, 3,5—热电偶, 4—加热烘箱 Fig.2 Schematic diagram of heater and cook-off test specimen 1—explosive, 2—shell, 3, 5—thermocouple, 4—heater |
从表 2中可以看出, 本文计算的点火时间与试验值存在-6.8%的偏差, 计算的药柱中心和壳体外壁温度与试验值分别存在-3.55%和-0.86%的偏差, 分析原因可能有以下三点:
(1) 试验中, 下端盖与凸起台阶紧密接触, 流入热量略小于壳体外壁。本研究为了简化计算, 将试件外侧以及上下表面全部施加第一类边界条件, 导致其总热量的积累要高于试验环境, 因此点火时间缩短, 中心点和边界点的温度也低于试验值。
(2) 试验件的壳体与炸药在局部存在少量间隙, 热量在此处传递以热对流和热辐射为主, 这与数值模拟中的无缝接触有一定区别, 也将导致偏差产生。
(3) 数值模拟中没有考虑RDX在高温下会发生一定程度的相变, 这也会导致偏差产生。
但在实际烤燃过程中, 壳体的导热系数远大于炸药, 少量间隙对总体温度影响较小, 并且仅有极少量炸药在温度急剧升高的区域可能发生相变, 表 2对比结果表明本研究建立的计算模型较为合理, 故以本程序为基础进行了RDX基PBX炸药烤燃试验数值模拟研究。
3 计算结果及分析 3.1 RDX基PBX炸药烤燃试验数值模拟针对装药尺寸为Φ40 mm×50 mm, 壳体厚度为3 mm的烤燃模型, 在升温速率为1 K·min-1条件下进行计算, 起爆点、中心点、边界点温度历程曲线如图 3所示。在加热初期, 热量由壳体向炸药内部传递, 壳体温度上升较快, 炸药内部温度变化较小, 在壳体和炸药内部存在明显的温度梯度, 其原因是壳体的热导率远大于炸药的热导率。随着时间推移, 热量逐渐积累, 起爆点温度在9790 s时刻反超边界点温度, 之后迅速升高, 直至9842 s时温度梯度无穷大, 计算终止, 此时炸药处于热失控状态, 即认为发生了点火。

|
图 3 三个特征点温度随时间的变化曲线 Fig.3 Temperature as a function of time at three characteristic points |
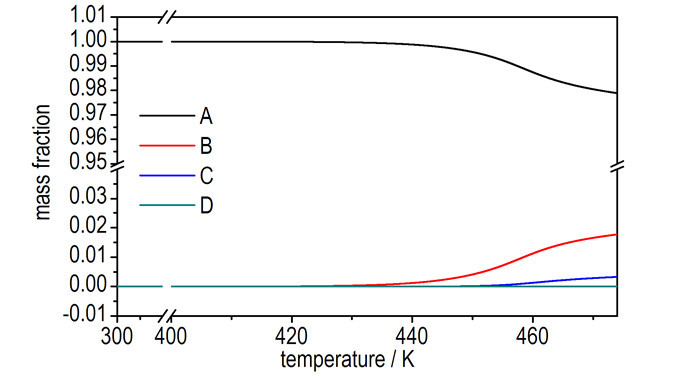
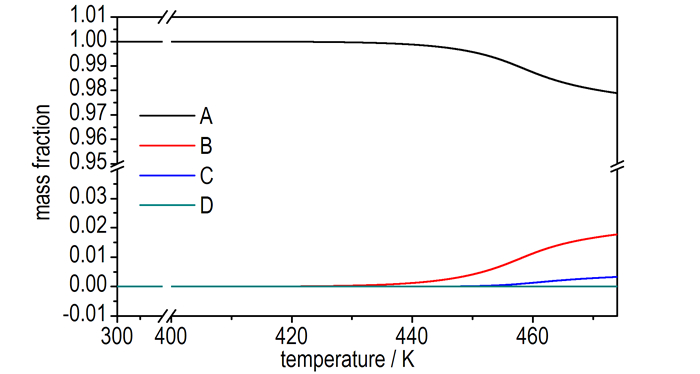
烤燃过程中, 点火区域组分含量曲线如图 4所示。在加热初期, 各物质的含量变化极小, 400 K时, 初级反应开始加快, 至457 K时, 有1%RDX发生初级分解反应; 与此同时, 固体中间产物B的含量逐渐增加, 在457 K时, 其含量为0.9%;次级反应由于固体中间产物B的含量较低, 故反应时间拖后, 在450 K左右开始才开始有明显变化; 460 K时, 第三步反应开始加快; 当气体终产物D的质量分数为0.006时, 在第三步反应强烈热效应的作用下, 引发点火。因此气体终产物的含量可以作为炸药能否点火的判据之一。
|
图 4 1 K·min-1时炸药点火区域各组分的质量分数 Fig.4 Mass fraction of each component in the ignition point of explosive at a heating rate of 1 K·min-1 |
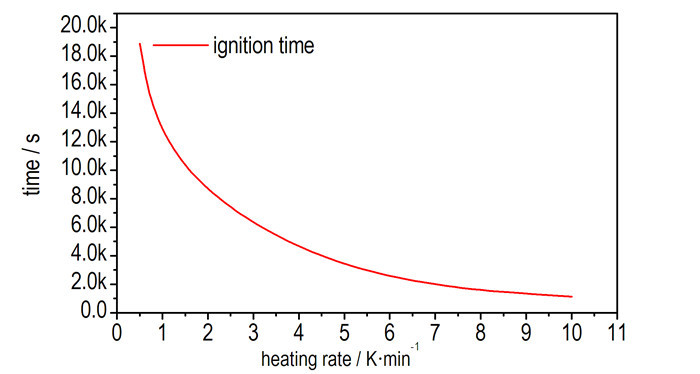
为了研究在烤燃过程中特征点温度和组分含量对升温速率的响应规律, 针对药柱尺寸Φ40 mm×50 mm, 壳体厚度为3 mm的模型, 计算了0.5, 1, 5, 10 K·min-1共4种升温速率下RDX基PBX炸药烤燃过程, 为了简化计算, 忽略升温速率对炸药热导率、比热容等参数的影响, 结果如图 5, 图 6所示。
|
图 5 点火时间随升温速率的变化曲线 Fig.5 Ignition time as a function of heating rate |

|
图 6 点火时刻的特征点温度随升温速率的变化曲线 Fig.6 Temperature of characteristic points at ignition time as a function of heating rate |
图 5为点火时间随升温速率变化的曲线。由图 5可见, 随着升温速率提高, 点火时间急剧衰减。图 6为点火时刻, 模型各特征点温度随升温速率变化的曲线。由图 6可见, 随着升温速率提高, 中心点的温度近似线性下降, 其原因是点火时间缩短, 中心点接受的热量随之减少; 起爆点温度基本不变, 其原因是该温度主要由热分解反应峰值决定, 与升温速率无关; 边界点温度增大, 其原因是升温速率的提高在边界点的作用最明显。由此表明:升温速率越低, 点火时环境温度越低, 炸药危险性越高。
图 7和图 8反映了在点火时刻, 起爆区域各分组份含量与升温速率的关系。由图 7可见, 随着升温速率减小, RDX炸药A和固体中间产物B含量变化较小。其原因是初级和次级反应对升温速率不敏感。由图 8可见, 随着升温速率减小, 气体中间产物C和气体终产物D明显增大。其原因是第三步强放热化学反应的反应程度增大。由此表明:升温速率越低, 气体终产物D的含量就越高, 炸药反应就越剧烈, 炸药的危险性就越高。

|
图 7 点火时刻起爆区域A, B组分含量随升温速率的变化曲线 Fig.7 Mass fraction of components A and B in the initiation area at ignition time as a function of heating rate |

|
图 8 点火时刻起爆区域C, D组分含量随升温速率的变化曲线 Fig.8 Mass fraction of components C and D in the initiation area at ignition time as a function of heating rate |
(1) RDX基PBX炸药在烤燃过程中, 400 K时初级分解反应开始加速, 450 K时次级分解反应明显发生, 进而诱导强放热的第三步化学反应, 表现为气体终产物的释放, 最终发生点火。
(2) 点火时间随升温速率的增加而急剧衰减, 中心点温度降低, 起爆点温度基本不变, 边界点温度增大。因此升温速率越低, 炸药点火的环境温度越低, 危险性越高。
(3) 升温速率越低, 在点火时刻, 起爆区域的气体终产物D的含量就越高, 第三步强放热反应就越剧烈, 后续的爆轰过程中, 释放的能量就更大, 炸药的危险性就越高。
本研究主要针对热传导机制作用下的烤燃过程数值模拟, 关于复杂问题, 如热辐射和热对流边界, 壳体力学响应等, 还需进一步探究。
| [1] |
Jones D A, Parker R P. Heat flow calculations for the small-scale cook-off bomb test, AD-A236829[R]. US: DTIC, 1991.
|
| [2] |
Howard W M, Nichols A L, Mcclelland M A. ALE3D Simulations of Gap Closure and Surface Ignition for Cookoff Modeling[M]. United States. Department of Energy, 2006.
|
| [3] |
Mcclelland M A, Maienschein J L, Howard W M, et al. ALE3D simulation of heating and violence in a fast cookoff experiment with LX-10[R]. Lawrence Livermore National Laboratory (LLNL), Livermore, CA, 2006.
|
| [4] |
王沛, 陈朗, 冯长根. 不同升温速率下炸药烤燃模拟计算分析[J].
含能材料, 2009, 17(1): 46-49. WANG Pei, CHEN Lang, FENG Chang-gen. Numerical simulation of cook-off for explosive at different heating rates[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(1): 46-49. |
| [5] |
陈朗, 王沛, 冯长根. 考虑相变的炸药烤燃数值模拟计算[J].
含能材料, 2009, 17(5): 568-573. CHEN Lang, WANG Pei, FENG Chang-gen. Numerical study of explosive cook-off with phase change[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(5): 568-573. |
| [6] |
张晓立, 洪滔, 秦承森, 等. 烤燃弹热点火的LS-DYNA数值模拟研究[J].
弹箭与制导学报, 2011, 31(5): 110-112. ZHANG Xiao-li, HONG Tao, QIN Cheng-cen, et al. LS-DYNA numerical simulation for thermal ignition of cook-off bomb[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(5): 110-112. |
| [7] |
陈科全, 黄亨建, 路中华, 等. 基于ABAQUS的PBX炸药烤燃试验数值计算[J].
火炸药学报, 2014, 37(2): 31-36. CHEN Ke-quan, HUANG Heng-jian, LU Zhong-hua, et al. Numerical calculation of cook-off test for PBX explosive based on ABAQUS[J]. Chinese Journal of Explosives and Propellants, 2014, 37(2): 31-36. |
| [8] |
McClelland M A, Tran T D, Cunningham B J, et al. Cookoff response of PBXN-109: material characterization and ALE3D model[C]//Proceedings of JANNAF 19th Propulsion Systems Hazards Subcommittee Meeting. 2000: 191.
|
| [9] |
牛余雷, 南海, 冯晓军, 等. RDX基PBX炸药烤燃试验与数值计算[J].
火炸药学报, 2011, 34(1): 32-37. NIU Yu-lei, NAN Hai, FENG Xiao-jun, et al. Cook-off test and its numerical calculation of RDX-based PBX explosive[J]. Chinese Journal of Explosives and Propellants, 2011, 34(1): 32-37. |
| [10] |
冯长根.
热爆炸理论[M]. 北京: 科学出版社, 1988: 97-117.
FENG Chang-gen. Theory of Thermal Explosion[M]. Beijing: Science Press, 1988: 97-117. |
Based on the self-written finite element software, change rule of the mass fraction of each components with temperature in the ignition area was explored.




