发射药的燃烧渐增性是改进压力平台、提高弹丸初速的关键技术之一。19孔制式发射药最大增面值达到1.7[1]。目前, 19孔发射药的生产采用挤出成型[2], 合理的模具结构是保证发射药质量的重要因素。随着现代军事的发展, 为了满足不同武器的使用需求, 对发射药改性的研究逐步深入[3-6], 挤出模具的结构需随之做出改变。模具设计不合理, 挤出的发射药会产生偏孔, 密度不均匀、产品质量不稳定、模具损坏等现象。传统的模具设计主要依靠设计经验和工程试验类比, 反复的试模和修模浪费了大量的人力物力, 生产效率低, 无法满足新型发射药配方研制需求。
随着计算机硬件和软件的发展, 数值模拟技术已广泛应用于聚合成型研究, 缩短了模具开发时间, 提高了设计准确性。秦升学等[7]模拟了聚合物熔体在机头的流动情况, 优化了阻流部分的结构, 实现了对厚度为0.12 mm的聚对苯二甲酸乙二醇酯(PET)薄膜厚度均匀性的控制。Mutlu等[8]模拟了线缆包覆挤出过程中自由挤出压力与线缆牵引共同驱动的聚合物熔体流动问题。张敏等[9]对两种聚合物熔体在共挤出流道内的流动进行了三维数值模拟, 研究了共挤出界面偏移的影响因素。Chitkara N R等[10]对非对称T型型材挤出成型过程进行研究, 对产品曲率和网格变形进行了预测。张丹丹等[11]对七孔药挤出过程进行了模拟计算, 研究了溶剂比、入口速度、成型温度对硝基胍发射药成型质量的影响。刘林林等[12]利用Polyflow软件得到了挤出条件对变燃速发射药药型尺寸一致性的影响规律。深入研究药料在流道内的流动过程有助于改善发射药的成型质量, 提高其性能。19孔发射药作为燃烧渐增性优良的火药, 对其成型过程及挤出模具的研究十分必要, 国内外尚未发现相关研究报告。
本研究针对发射药某高黏度配方, 设计了19孔挤出模具。采用ANSYS软件对其成型过程进行了数值模拟, 分析了初始模具流道内药料的流动情况, 获得模具压缩比、成型段长度、针架结构对药料流动的影响规律。对模具进行优化设计, 并对比分析了优化前后的流道内药料的流动状态。根据优化结果加工新模具并进行实验, 成功生产出燃烧稳定的19孔发射药。
2 模型建立 2.1 流道结构19孔发射药挤出模具主要分为压缩段、针架和模针、成型段, 如图 1所示。流道横截面如图 2所示。压缩比是进药面积与有效出药面积之比, 针架和模针决定发射药内孔的直径和位置, 成型段决定最终产品的形状。19孔发射药挤出模具的模针共有三层, 第一层(中心)1根, 第二层6根, 最外层12根。

|
图 1 流道结构示意图 Fig.1 Schematic diagram of flow channel |
|
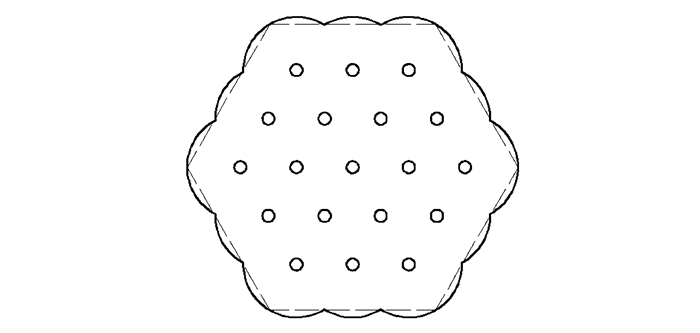
图 2 流道横截面 Fig.2 Cross section of flow channel |
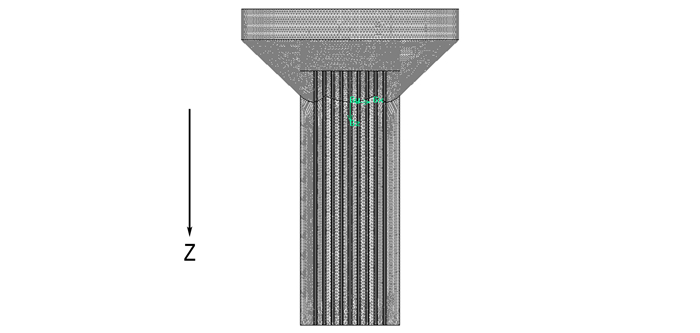
为了提高计算效率, 将成型段由花边形简化为六边形, 如图 2中虚线所示。图 3为初始模具流道有限元模型, z轴方向为药料流动方向。
|
图 3 流道有限元模型 Fig.3 Finite element model of flow channel |
作为一种特殊的高分子材料, 发射药的挤出流动特性遵循以下方程[13]:
质量守恒方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \rho \;\nabla \cdot u = 0 $ | (1) |
动量守恒方程:
| $ \rho (\frac{{\partial u}}{{\partial t}} + u\cdot\nabla u) = \nabla \cdot\sigma + \rho g $ | (2) |
能量守恒方程:
| $ \rho {c_p}\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = k\nabla \cdot(\nabla T) + \tau :\nabla u $ | (3) |
式中, ρ为流体密度, g·cm-1; u为流体速度, m3·s-1; ∇为Hamilton微分算子; σ为表面应力, Pa; cp为等压比热, J·kg-1·K-1; k为材料导热系数, W·m-1·K-1; τ为偏应力张量, Pa。
求解上述基本方程须针对工程问题实际情况进行适当的假设简化处理。考虑药料的特性和稳定挤出时的工艺条件, 可做如下假设[14]:
(1) 药料是不可压缩的稳态层流;
(2) 流场稳定、等温;
(3) 药料在流道壁上无滑移, 即其各个速度分量为零;
(4) 不计药料重力和惯性力的影响。
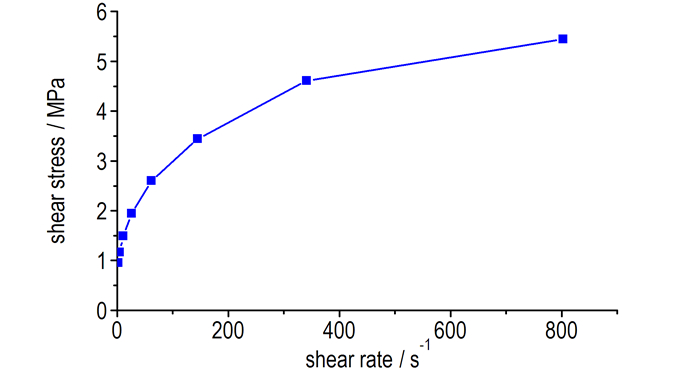
2.3 材料物性参数采用Malwern公司Roand RH2200型毛细管流变仪测量该配方发射药的流变性能, 25 ℃下剪切应力τ和剪切速率
|
图 4 发射药剪切应力-剪切速率曲线 Fig.4 Shear stress vs shear rate curve of propellant flow |
边界条件设置如下: (1)流道入口采用速度入口边界条件, 入口线速度为1.50×10-3 m·s-1; (2)流道出口采用压力出口边界条件, 出口压力为1 atm; (3)其余均为无滑移壁面。
3 初始模具挤出过程模拟结果分析初始模具压缩比为5.78, 成型段长度36.0 mm。利用ANSYS软件模拟发射药药料在初始模具中的流动过程, 分析结果见图 5、图 6、图 7。
|
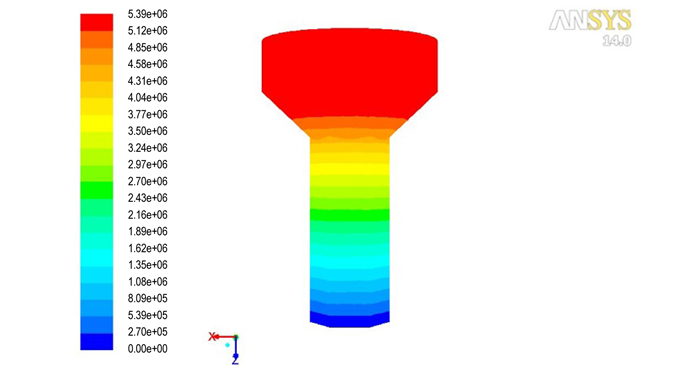
图 5 流道内压力分布云图 Fig.5 Pressure distribution in the flow channel |
|
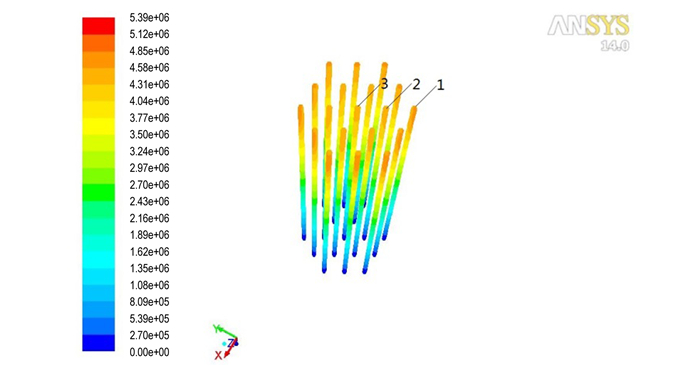
图 6 模针压力分布云图 Fig.6 Pressure distribution on the die pin |
|
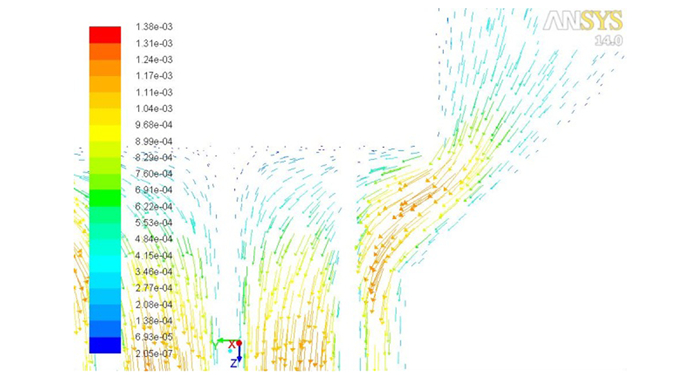
图 7 y=0截面局部速度矢量图 Fig.7 Partial velocity distribution on the y=0 cross section |
图 5为流道内压力分布云图。可见, 流道内压力最大值出现在入口处, 为5.39 MPa。沿着药料的流动方向, 流道内的压力逐渐减小, 流道内最大压力降发生在成型段, 压力减小了4.58 MPa。图 6为模针所受压力分布云图。可见, 模针所受最大压力出现在压缩段。模针在压缩段各个方向受到的压力不均匀, 最大压力达到4.85 MPa, 位于最外层模针1的外侧, 而其内侧压力为4.31 MPa。这导致模针1受到的合力最大, 位于第二层的模针2受力略小, 中心模针均匀受力。
图 7为y=0截面局部速度矢量图。可见, 从压缩段到成型段, 产生了较强的收敛流动, 药料流动方向发生变化。因压缩比较大, 在压缩段药料径向流动速度增加, 挤进内层模针之间。压缩段针架附近药料发生绕流, 流动方向、速率变化较大。最外层模针与针架连接位置附近的药料流动方向几乎水平, 压缩段的速度最大值出现在最外层模针附近, 为1.24×10-3 m·s-1, 最大径向分速度为1.06×10-3 m·s-1。在此流动状态下, 模针受到剧烈冲击, 易在压缩段发生断裂。
4 流道结构对药料流动的影响及模具优化 4.1 流道结构对药料流动的影响为了获得合理的模具结构参数, 分别模拟了入口线速度为1.50×10-3 m·s-1时, 不同压缩比、不同成型段长度和针架结构对药料流动规律的影响, 结果如表 1、表 2和表 3所示。
| 表 1 压缩比对药料流动的影响 Tab.1 Effect of compression ratio on propellant flow |
| 表 2 成型段长度对药料流动的影响 Tab.2 Effect of length of forming section on propellant flow |
| 表 3 针架结构对药料流动的影响 Tab.3 Effect of structure of pin holder on propellant flow |
表 1为不同压缩比时, 流道内的各处压力和最大径向分速度。比较发现, 在压缩比大于2.95时, 随着压缩比的减小, 流道内最大压力pmax、模具所受最大压力p′max、成型段入口中心处压力p均有所减小。压缩比减小为1.89时, 药料在压缩段受到较大的压力, 达到11.2 MPa, 但是成型段入口处压力减小为1.68 MPa。这是因为压缩比过小, 药料从流道入口进入成型段时的流道变窄, 压缩段阻力增大, 压力升高。同时进入成型段与模针之间的药料减少, 因此p′max和p较小。这种情况会引起药料在压缩段产生不稳定流动, 模具中心压力过低, 影响发射药内部结构。表 1显示, 随着压缩比的减小, 最大径向分速度v减小。因此可以通过调整压缩比来改变流道内各处压力及最大径向分速度。
表 2显示, 成型段长度对pmax、p′max和p影响较大, 对v几乎没有影响。这与药料在流道内的流程有关, 流程越长, 阻力越大, 成型压力越大, 因此可以通过缩短成型段长度来减小流道内各处压力。当成型段长度为16 mm时, p低于2 MPa, 实验表明在此条件下19孔发射药各部分密度不一致, 燃烧性能不稳定。因此, 该配方19孔挤出模具成型段长度不可小于16 mm。
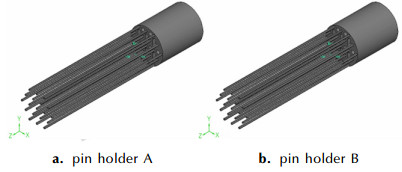
表 3为针架结构对药料流动的影响。针架A如图 8a所示, 药料从针架周围进入模针之间。针架B如图 8b所示, 药料从针架周围和针架上的孔道流入中心模针之间。表 3显示, 与压缩比、成型段长度相比, 针架结构的改变对流道内各处压力的影响相对较小, 但对最大径向分速度影响较大。选择结构B可在降低流道内各处压力的同时大幅度减小v。
|
图 8 针架与模针结构示意图 Fig.8 Schematic diagram of pin holder and die pins |
根据计算结果, 模具的优化分为三部分:首先, 通过减小压缩比, 减小压力和径向分速度; 其次, 缩短成型段长度, 减小流动阻力; 最后, 改变针架结构, 减小最大径向分速度。根据优化方案, 选取新模具压缩比减小为4.25, 成型段长度减少为26.0 mm, 选取模具针架结构B, 降低流道内最大压力和模针所受最大压力的同时确保流道中心的压力。建立三维模型划分有限元网格并对挤出过程进行数值模拟, 材料物性参数与边界条件与初始模具模拟设置一致。
4.3 优化前后模具模拟结果对比 4.3.1 压力分布分析优化后流道内压力最大值同样出现在入口处, 为3.21 MPa, 与初始模具相比, 下降40.45%。成型段入口中心压力为2.24 MPa, 满足发射药成型要求。成型段缩短以后压力降减小为2.40 MPa。模针所受最大压力由4.85 MPa下降到2.88 MPa, 下降了40.62%。流道横截面的压力标准差反映了流道内压力分布的均匀性, 是衡量挤出发射药密度的重要参数。选择横截面形状变化最大的成型段入口处, 对比模具优化前后此处的压力分布, 如图 9所示。初始模具最外侧模针两侧可以明显看到压力分界线, 优化后, 压力分界线向中心移动, 分界线两侧压差减小。初始模具该截面压力标准差为0.84 MPa, 而优化后模具截面压力标准差为0.44 MPa, 减小了47.62%。这说明模具优化之后, 流道内压力分布均匀性提高。

|
图 9 成型段入口压力分布云图 Fig.9 Pressure distribution of forming section inlet |
径向合力和轴向合力是造成模针断裂的主要原因之一。优化前后模针在压缩段所受径向合力见表 4, 在挤出过程中所受轴向合力见表 5。可见, 外侧模针所受径向合力减小37.45%, 轴向合力减小42.90%。优化后, 流道内压力减小, 模针所受合力减小, 可有效减小模针的变形程度, 避免损坏。
| 表 4 模针在压缩段所受径向合力 Tab.4 Radial force on die pin in the compression section |
| 表 5 模针所受轴向合力 Tab.5 Axial force on die pin in the compression section |
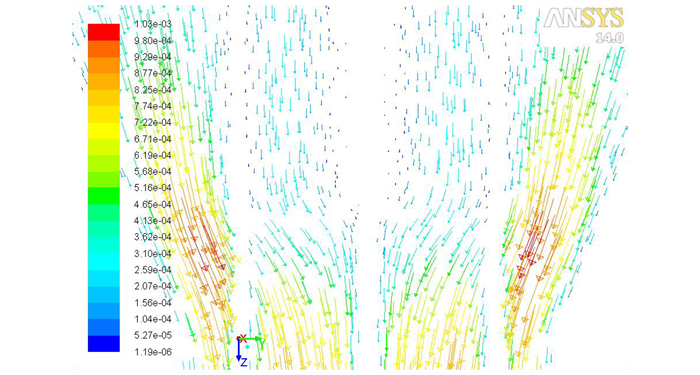
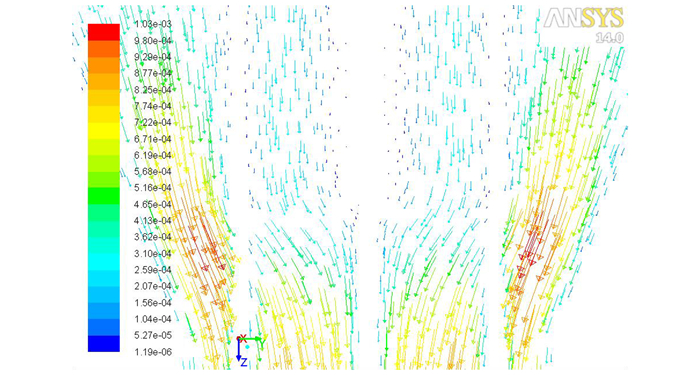
模具优化后, 从压缩段到成型段, 药料流动如图 10所示。对比图 7, 模具优化后药料在针架附近受到的径向力减小, 从轴向进入成型段的药料比例增加。在入口线速度相同的条件下, 优化后的模具流道内最大流速为1.03×10-3 m·s-1, 与初始模具最大流速1.38×10-3 m·s-1相比, 减小了25.36%。速度减小的原因是压缩比减小, 出口面积不变, 入口线速度相同, 体积流量减小。故在优化前后出口没有改变的情况下, 线速度减小。优化之后, 压缩段最大径向分速度减小为3.50×10-4 m·s-1, 与初始模具相比减小了66.98%, 大幅度降低模针所受冲击。
|
图 10 x=0截面局部速度矢量图 Fig.10 Partial of velocity distribution on x=0 cross section |
成型段出口处速度分布的均匀性是衡量挤出发射药质量的重要指标。选取出口横截面上各个节点速度值计算出口速度标准差来衡量出口挤出流动平衡。对比优化前后模具的出口速度分布, 速度最大值均出现在模针之间, 分别是1.30×10-3 m·s-1、9.68×10-4 m·s-1, 出口速度标准差分别为2.97×10-4 m·s-1、2.24×10-4 m·s-1。模具优化后, 出口速度分布均匀性提高24.58%。
4.4 实验验证 4.4.1 挤出成型19孔发射药根据上文确定的流道结构, 设计制造挤出模具。分别采用优化前后的模具挤出成型19孔发射药。控制油压机冲头速度保持模具入口线速度均为1.50×10-3 m·s-1。
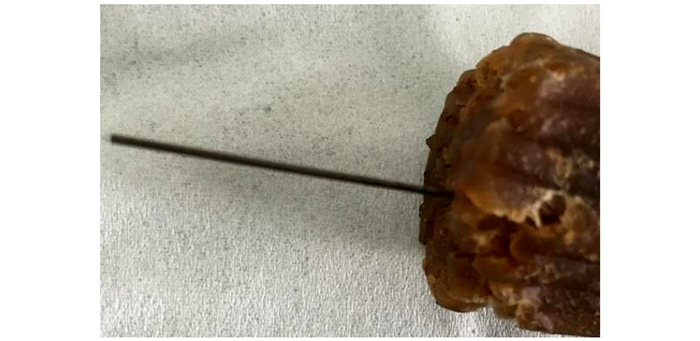
实验测得初始模具挤出过程的最大压力为5.48 MPa, 计算结果与实验结果相比偏差1.64%, 说明仿真方法及边界条件设置是正确的。模具损坏发生在压缩段, 模针断裂, 如图 11所示。可见, 挤出的产品表面不光滑, 出现不规则形状的粗糙条纹。造成这一现象的原因之一为该配方药料黏度高, 挤出过程所需压力大。此外, 初始模具流道压缩比过大, 成型段过长, 导致流动阻力过高。药料与流道壁面的外摩擦力高, 流道内压力分布不均匀, 药料各部分受到的剪切应力不一致, 药料内部各处的剪切粘度产生差异, 使边界层各处产生不同的摩擦应力, 导致药料各点的旋转不一, 造成表面疵病。
|
图 11 初始模具挤出19孔发射药 Fig.11 19-hole propellant extruded by original die |
优化后模具挤出实验测得挤出最大压力是3.48 MPa, 较计算值高8.41%。利用该模具挤出的19孔发射药, 表面光滑, 内孔分布均匀, 如图 12所示, 没有出现初始模具挤出产品的扭曲变形、瑕疵、模针断裂、弧厚不均匀等缺陷, 说明挤出均匀性好, 模具流道结构设计合理。

|
图 12 优化后模具挤出19孔发射药 Fig.12 19-hole propellant extruded by optimized die |
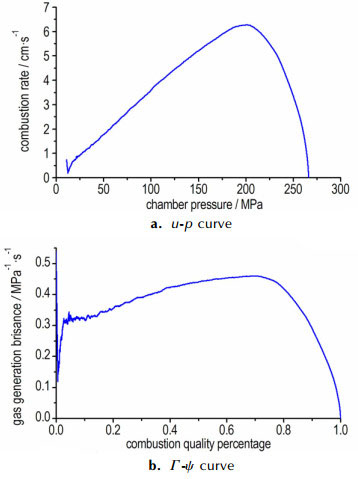
对优化后模具挤出的19孔发射药进行100 mL密闭爆发器定容燃烧实验, 装填密度0.2 g·cm-3, 点火药为2#硝化棉, 质量为1.1 g, 所得燃速u与压力p的关系、燃气生成猛度Γ与已燃百分比ψ的关系如图 13所示。由图 13a所示, u-p的曲线没有异常拐点, 说明优化后模具挤出的19孔发射药燃烧稳定, 发射药各部分的组成、密度一致, 内部结构没有缺陷。
|
图 13 优化后模具挤出19孔发射药燃烧性能 Fig.13 Combustion performance of 19-hole propellant extruded by optimized die |
由图 13b所示, 燃气生成猛度Γ随已燃百分比ψ的增加逐渐增加, 在ψ=0.72时, Γ达到最大值, 随着燃烧的继续, Γ开始下降, 显示出良好的增面燃烧效果。
5 结论(1) 初始模具挤出失败的原因是:药料所受流动阻力高、模针局部压力大和药料压缩段径向分速度大。
(2) 三个关键参数对药料流动的影响是:压缩比减小, pmax、p′max、p及v均减小; 成型段长度缩短, pmax、p′max和p均减小, v几乎不变; 选择针架结构B可在减小pmax、p′max和p的同时大幅度减小v。
(3) 针对19孔发射药挤出成型模具的优化方案为:模具压缩比为4.25, 成型段长度为26.0 mm, 并选用针架B。数值模拟结果显示, 优化后流道内最大压力减小40.45%, 最外侧模针压缩段所受径向合力减小37.45%, 外侧模针所受轴向合力减小42.90%, 压缩段药料最大径向分速度减小66.98%, 流道内压力分布均匀性提高47.62%, 出口速度分布均匀性提高24.58%。
(4) 优化后的模具挤出成型的19孔发射药表面光滑, 内孔分布良好, 克服了初始模具挤出产品的扭曲变形、瑕疵、模针断裂、弧厚不均匀等缺陷。定容燃烧实验表明, 采用新模具加工的发射药各部分组成均匀, 没有内部缺陷, 渐增性优良。
| [1] |
王泽山, 何卫东, 徐复铭.
火药装药设计原理与技术[M]. 北京: 北京理工大学出版社, 2006: 219-222.
WANG Ze-shan, HE Wei-dong, XU Fu-ming. Propellant charge design principles and technique[M]. First edition, Beijing: Beijing institute of technology press, 2006: 219-222. |
| [2] |
赵宝昌, 邢玉仁, 邓庆才, 等.
硝基胍发射药[M]. 北京: 兵器工业出版社, 1989: 28-44.
ZHAO Bao-chang, XING Yu-ren, DENG Qing-cai, et al. Nitroguanidine propellant[M]. First edition, Beijing: Weaponry industry press, 1989: 28-44. |
| [3] |
丁海琴, 肖乐勤, 菅晓霞, 等. GAP热塑性弹性体共混增韧硝化棉研究[J].
固体火箭技术, 2012, 35(4): 495-499. DING Hai-qin, XIAO Le-qin, JIAN Xiao-xia, et al. Research of blends of gap-based polyurethane elastomer and NC[J]. Journal of Solid Rocket Technology, 2012, 35(4): 495-499. |
| [4] |
姚月娟, 刘少武, 王锋, 等. NG含量对改性单基药燃烧渐增性的影响[J].
含能材料, 2013, 21(3): 343-346. YAO Yue-juan, LIU Shao-wu, WANG Feng, et al. Effect of nitroglycerine content on combustion progressivity of modify single base propellant[J]. Chinese Journal of Energetic Materias(Hanneng Cailiao), 2013, 21(3): 343-346. |
| [5] |
何卫东, 魏晓安, 王泽山. 热塑性弹性体在太根发射药中的应用研究[J].
含能材料, 2010, 18(1): 80-82. HE Wei-dong, WEI Xiao-an, WANG Ze-shan. Application of thermoplastic elastomer to triethylene glycol dinatrate propellant[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2010, 18(1): 80-82. |
| [6] |
赵毅, 黄振亚, 刘少武, 等. 改善高能硝胺发射药力学性能研究[J].
火炸药学报, 2005, 28(3): 1-3. ZHAO Yi, HUANG Zhen-ya, LIU Shao-wu, et al. study of improving mechanical performance of high-energy nitroamine propellant[J]. Chinese journal of explosives and propellants, 2005, 28(3): 1-3. |
| [7] |
秦升学, 杨迁, 徐新民. PET薄膜挤出成型有限元模拟和阻流分析[J].
高分子材料科学与工程, 2012, 28(7): 179-183. QIN Sheng-xue, YANG Qian, XU Xing-ming. Finite element simulation of PET film extrusion and analysis of choked flow[J]. Polymer materials science and engineering, 2012, 28(7): 179-183. |
| [8] |
Mutlu I, Townsend P, Webster M F. Simulation of cable-coating viscoelastic flows with coupled and decoupled schemes[J].
Journal of Non-Newtonian Fluid Mechanics, 1998, 74: 1-23. DOI:10.1016/S0377-0257(97)00069-4 |
| [9] |
张敏, 孙胜, 贾玉玺. 基于有限元方法的聚合物共挤出界面形成过程数值研究[J].
应用基础与工程科学学报, 2008, 16(5): 712-718. ZHANG Min, SUN Sheng, JIA Yu-xi. Numerical analysis of the polymer coextrusion interface based on the finite element method[J]. Journal of Basic Science and Engineering, 2008, 16(5): 712-718. |
| [10] |
Chitkara N R, Celik K. Extrusion of non-symmetric T-shaped sections. Analysis and some experiments[J]. Mechanical Sciences, 2001, 43(12): 2961-2987.
|
| [11] |
张丹丹, 何卫东. 硝基胍七孔发射药挤压成型过程的数值模拟[J].
火炸药学报, 2014, 36(6): 82-86. ZHANG Dan-dan, HE Wei-dong. Numerical simulation of 7-hole nitroguanidine-base gun propellant in extrusion forming process[J]. Chinese Journal of Explosives and Propellants, 2014, 36(6): 82-86. |
| [12] |
刘林林, 马忠亮, 高可政, 等. 变燃速发射药挤出过程中药料流动计算研究[J].
含能材料, 2010, 18(5): 583-586. LIU Ling-ling, MA Zhong-liang, GAO Ke-zheng, et al. Computational study of flow for outside layer of variable-burning rate propellant during extrusion[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2010, 18(5): 583-586. |
| [13] |
周彦豪.
聚合物加工流变学基础[M]. 第一版, 陕西: 西安交通大学出版社, 1988: 123-166.
ZHOU Yan-hao. Polymer processing and rheology base[M]. The first edition, Shaanxi: Xi'an jiaotong university press, 1988: 123-166. |
| [14] |
MU Yue, ZHAO Guo-qun. Numerical study of nonisothermal polymer extrusion flow with a differential viscoelastic model[J].
Polymer Engineering and Science, 2008, 48(2): 316-328. DOI:10.1002/(ISSN)1548-2634 |
Simulation of the propellant flow in a 19-hole die channel provides the basis for optimization. The new die was processed and used to extrude propellant successfully.




