2. 中国工程物理研究院化工材料研究所, 四川 绵阳 621999
2. Institute of Chemical Materials, CAEP, Mianyang 621999 China
高聚物粘结炸药(Polymer Bonded Explosive, PBX), 在压制过程中会发生位移、变形甚至断裂等各种力学行为, 但是这些力学行为很难直接观察到, 故人们难以明确其成型机理。为表征复合含能材料的压制成型特性, 许多学者通过数值模拟方法[1-3]计算炸药不同组分中力学参量的变化, 得到压制过程的力学行为状态及模拟数据, 对改进压制工艺和控制炸药质量具有重要意义。
PBX的力学性能、热力学性能和化学性质都与细观尺度上的物理和化学过程直接相关[4], 因此在细观尺度上研究PBX的压制过程对于理解它的力学性能有重大意义。目前, 工程上常用的研究PBX力学行为的Lagrangian有限元方法(Finite Element Method, FEM)是基于连续介质的力学方法[5]。如兰琼等[2]利用有限元计算方法, 对奥克托今(HMX)基PBX炸药温压时效处理过程的加热加压阶段进行模拟, 得到处理过程中炸药件尺寸变化规律, 并推导出炸药件密度变化量, 由此预测温压时效处理对PBX的作用效果; 张涛等[6]运用基于有限元方法对PBX粉末温压成型过程进行了数值模拟, 获得了粉末体几何形变、应力场及相对密度分布等相关数据等。有限元方法的优点是计算速度快, 能够在接近于工程的宏观尺度上对材料的性质进行研究, 缺点是不能有效地在计算中考虑微观结构的性质, 且在处理材料极大变形问题时, 网格发生扭曲、畸变和缠绕, 重新划分网格非常困难, 计算精度严重下降。近些年来, 无网格法被提出并成为研究热点, 常用的无网格法有十几种, 其基本思想是将连续体离散为质点单元的形式, 在计算过程中, 所有信息都由这些质点来表达, 避免了网格重新划分的难题。作为无网格法之一, 物质点法(Material Point Method, MPM)本质上是一个基于粒子的计算方法[7], 相对其他基于网格的数值方法具有更高的效率和精度, 同时在处理大变形问题以及一些带有接触的问题时比有限元法具有显著的优势[8]。
因此, 本研究主要应用MPM方法模拟细观尺度下HMX基PBX压制成型过程的力学行为, 重点分析HMX基PBX压制成型过程中炸药颗粒变形、颗粒间的应力传递以及温度变化等细观力学行为。
2 MPM的基本理论物质点法在计算时满足质量守恒方程和动量守恒方程[7]:
| $ \frac{{{\rm{d}}\rho }}{{{\rm{d}}t}} + \rho \nabla \cdot v = 0 $ | (1) |
| $ \rho a = \nabla \cdot \sigma + \rho b $ | (2) |
式中, ρ为材料密度, kg·m-3; a是加速度, m·s-2; v是质点速度, m·s-1; b是单位体积力, N; σ是柯西应力张量, Pa。
将基于背景网格的有限元形函数, 试函数ω带入动量守恒方程(3)并在区域Ω上积分, 可以得到动量方程的虚功方程[7]:
| $ \int\limits_\Omega {\rho a \cdot \omega {\rm{d}}V} + \int\limits_\Omega {\rho {\sigma ^s}:\nabla {\rm{d}}V}-\int\limits_\Omega {\rho b \cdot \omega {\rm{d}}V}- \int\limits_\mathit{\Gamma } {\tau \cdot \omega {\rm{d}}S} = 0 $ | (3) |
式中, dV和dS分别表示微分体积元和面积元; σs是比应力σs=σ/ρ; Γ为指定的应力边界; 边界应力为τ; 在指定位移边界上的试函数ω=0。
由于把连续体离散成具有集中质量的物质点, 在整个计算过程中每个物质点的质量保持不变, 故自动满足质量守恒方程。因此, 密度可以表示为[7]:
| $ \rho (x, t) = {\rm{ }}\sum\limits_{p = 1}^{{N_p}} {{m_p}\delta (x-{x_p})} $ | (4) |
式中, mp是物质点p的质量, g; δ是狄拉克函数; xp是物质点p的坐标; Np是物质点总数。
物质点数量和质量在整个计算过程中始终不变, 质量守恒方程自动满足。在求解动量方程时, 质点和背景完全固连, 随着背景网格一起运动, 因此可通过建立在背景网格节点上的有限元形函数Ni(x)实现物质点和背景网格节之间信息的映射。网格节点和物质点这件变量的映射关系为[9]:
| $ {\psi _p} = \sum\limits_{i = 1}^{{n_u}} {{\psi _i}{N_i}({x_p})} $ | (5) |
式中, ψp表示物质点携带的变量; ψi表示网格节点上的变量; nu表示单元节点数; xp表示物质点的坐标。
最终(3)式可写成下面的节点离散形式:
| $ {m_i}{a_i} = f_i^{{\rm{int}}} + f_i^{{\rm{ext}}} $ | (6) |
式中节点质量为:
| $ {m_i} = {\rm{ }}\sum\limits_{p = 1}^{{N_p}} {{m_p}{N_i}({x_p})} $ | (7) |
内力:
| $ f_i^{{\rm{int}}} = - {\rm{ }}\sum\limits_{p = 1}^{{N_p}} {{m_p}\sigma _p^s \cdot \nabla N{|_{{x_p}}}} $ | (8) |
外力:
| $ f_i^{{\rm{ext}}} = \sum\limits_{p = 1}^{{N_p}} {{m_p}b{N_i}({x_p})} + \int\limits_\mathit{\Gamma } {{N_i}\left( {{x_p}} \right)t{\rm{d}}\mathit{\Gamma }} $ | (9) |
(6) 式为动量方程在网格节点上的离散形式, 这里采用显式积分进行求解, 具体步骤可以参考文献[7, 9]。
物质点法实现了物质点到网格和网格到物质点的2次映射, 物质点的应力可利用本构方程由式(5)和材料方程更新, 得到下一时刻物质点所携带的变量。物质点法的背景网格只在每个时间步内和物体固连, 在每个时间步结束时, 丢弃已经变形的背景网格, 这样避免了传统的有限元法中背景网格固定不动, 造成网格的畸变和缠结。
3 PBX压制数值模拟 3.1 PBX细观结构模型图 1a为HMX基PBX炸药在细观结构显微镜照片[10], 图 1a中显示PBX炸药颗粒的等效直径最大为0.2 mm, 粘结剂厚度约为0.01~0.05 mm。其中HMX颗粒大小、形状各不相同, 分布也极其不规则, HMX颗粒之间还存在粘结剂。在如此复杂的PBX炸药细观结构条件下, 建立一种直接反应炸药细观结构的模型存在一定的难度。PBX炸药是由炸药颗粒和粘结剂按一定的比例混合压制成型的, 在细观计算模型的构建中需要把PBX炸药压制成型过程考虑进去。

|
图 1 PBX炸药细观结构显微镜照片和炸药颗粒分布 Fig.1 Micrographs of the microstructure of PBX explosives and the distribution of explosive particles |
再利用图像处理技术, 将文献[10]中细观结构显微镜照片(图 1a)构建成较合理的PBX炸药细观结构模型(图 1b)。在细观结构计算模型的构建中, 将杂乱的晶体颗粒近似成圆形, 同时用粘结剂对颗粒外表层进行包裹。在圆形近似的过程中, 密集的粒径分布也被近似成稀疏的分布。这样的抽象近似对实际力学性能的影响还需进一步研究。
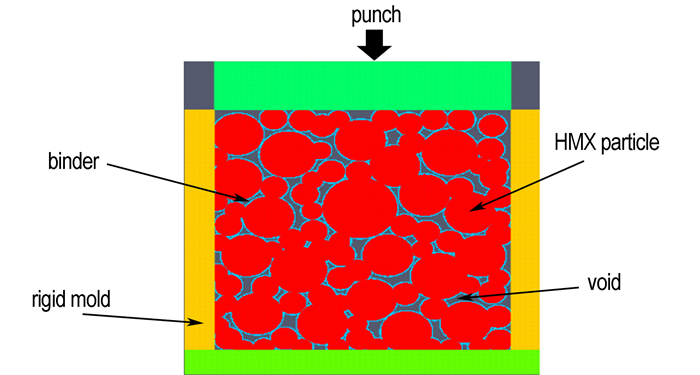
3.2 计算模型及方法由PBX炸药颗粒分布模型图(图 1b), 设计基于物质点法计算模型图, 如图 2所示。模型由刚性压头、刚性模具、炸药颗粒HMX和粘接剂Estane组成。压头的压制面设为刚性加压面, 模具内壁设为刚性约束面。红色的圆形粒子代表炸药颗粒, 炸药颗粒外表覆盖的一层蓝色物质为Estane粘结剂。炸药颗粒之间存在着少许孔隙, 孔隙中为空物质。模型中共有90个直径范围为0.02~0.2 mm的炸药颗粒, 颗粒之间紧密排布, 外层为厚度为0.005~0.010 mm的Estane粘结剂, HMX的体积分数为85%, 粘结剂体积分数为6%, 其余体积为孔隙。模型中, 刚性压头以0.3 m·s-1的速度向下压缩炸药, 炸药和周围环境的初始温度均为353.15 K, 模拟时间设为1 ms。
|
图 2 计算模型图 Fig.2 Calculation model |
模型中HMX颗粒采用弹塑性材料模型和Grüneisen状态方程描述。压头和模具材料为刚性。弹塑性材料模型的应力表示为[11]:
| $ \sigma = {\rm{[}}1 + \left( {\varepsilon /C} \right)1/P]({\sigma _0} + \beta {E_p}\varepsilon _p^{{\rm{eff}}}) $ | (10) |
式中, σ为应力, MPa; σ0为初始屈服应力, MPa; ε是应变率, C和P是Cowper-Symond应变率参数, εpeff是有效塑性应变, Ep是是塑性硬化模量, β是硬化参数。Grüneisen方程为[11]:
| $ \begin{array}{l} p = \frac{{\rho {c^2}\mu {\rm{[}}1 + \left( {1 - {\gamma _0}/2} \right)\mu - \alpha {\mu ^2}/2]}}{{[1 - \left( {{s_1} - 1} \right)\mu - {s_2}{\mu ^2}/\left( {\mu + 1} \right) - {s_3}{\mu ^3}/\left( {\mu + 1{^2}} \right)]}} + \\ \;\;\;\;\;\;\;\left( {{\gamma _0} + \alpha \mu } \right)E \end{array} $ | (11) |
式中, p为压力, MPa; μ=ρ/ρ0-1=1/Vr-1; c代表常温常压无扰动状态声速, m·s-1; ρ0为初始密度, kg·m-3; Vr为相对体积, m3; γ0为Grüneisen常数; E为内能, J; s1、s2和s3为冲击波波速-波后粒子速度曲线的斜率系数; α为一阶体积修正因数。HMX颗粒材料模型参数见表 1[12]。
| 表 1 HMX材料模型参数 Tab.1 The model parameters of HMX |
模型中粘结剂为Estane, 采用Prony级数形式的粘弹性本构模型和Tait状态方程, Prony级数形式粘弹性模型的应力表示为[13]:
| $ \sigma = \int_0^t {2G\left( {t-\tau } \right)\frac{{{\rm{d}}e}}{{{\rm{d}}\tau }}{\rm{d}}\tau } + I\int_0^t {K\left( {t-\tau } \right)\frac{{{\rm{d}}\Delta }}{{{\rm{d}}\tau }}{\rm{d}}\tau } $ | (12) |
式中, σ为应力, MPa; G(t)为剪切松弛核函数, e为应变偏量部分(剪切变形), Δ为应变体积部分(体积变形), t为当前时间, s; τ为过去时间, s; I 为单位张量。用Prony级数表示粘弹性属性的基本形式为[11]:
| $ G\left( t \right) = {G_\infty } + \sum\limits_{i = 1}^{{n_G}} {{G_i}{\rm{exp}}\left( {-\frac{t}{{\tau _i^G}}} \right)} $ | (13) |
| $ K\left( t \right) = {K_\infty } + \sum\limits_{i = 1}^{{n_K}} {{K_i}{\rm{exp}}\left( {-\frac{t}{{\tau _i^K}}} \right)} $ | (14) |
式中, G∞和Gi是剪切模量, MPa; K∞和Ki是体积模量, MPa; τiG和τiK是各Prony级数分量的松弛时间(Relative time), s。Tait状态方程为[13]:
| $ V\left( {p, T} \right) = V\left( {0, T} \right)[1-C{\rm{ln}}(1 + \frac{p}{{B\left( T \right)}})] $ | (15) |
| $ B\left( T \right) = CK(0, T) $ | (16) |
式中, p为压力, MPa; T为温度, K; C=0.0894是通用的Tait常数; V(0, T)是在0压下由温度决定的体积函数; K(0, T)是在0压下温度决定的体积模量函数。粘接剂Estane材料模型参数见表 2[12]。
| 表 2 Estane材料模型参数 Tab.2 The model parameters of Estane |
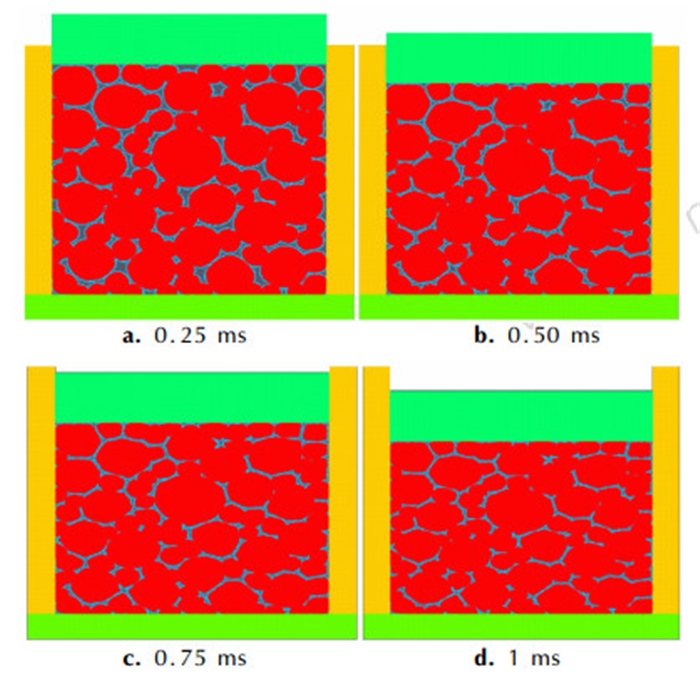
刚性压头以0.3 m·s-1的速度从上往下压缩时, PBX炸药体系在不同时刻的变形情况如图 3所示。数值模拟结果表明, PBX在压缩的过程中, 其颗粒形状是不断变化的。图 3a和图 3b为压缩过程中的整合阶段, 炸药颗粒重新排列, 形成接触挤压。在图 3a中, 位于接触面的炸药颗粒首先受到刚性压头的挤压, 炸药颗粒向下的运动, 颗粒间的缝隙不断减小。在0.50 ms时, 炸药颗粒已趋于压实的状态, 各颗粒之间接触挤压已经基本形成。图 3c和图 3d表示炸药颗粒的巩固阶段发生塑性形变的过程。在图 3c中炸药体系压缩到0.75 ms时, 炸药颗粒之间均受到不同程度力的挤压, 发生塑性变形, 颗粒轮廓明显改变。一直压缩到图 3d的塑性变形的状态。炸药颗粒的特征基本消失, 形成密实整体, 压制过程变为对炸药整体的压缩作用。
|
图 3 PBX炸药压制过程中不同时刻的变形模拟结果 Fig.3 Deformation simulation results of PBX at different times during compression |
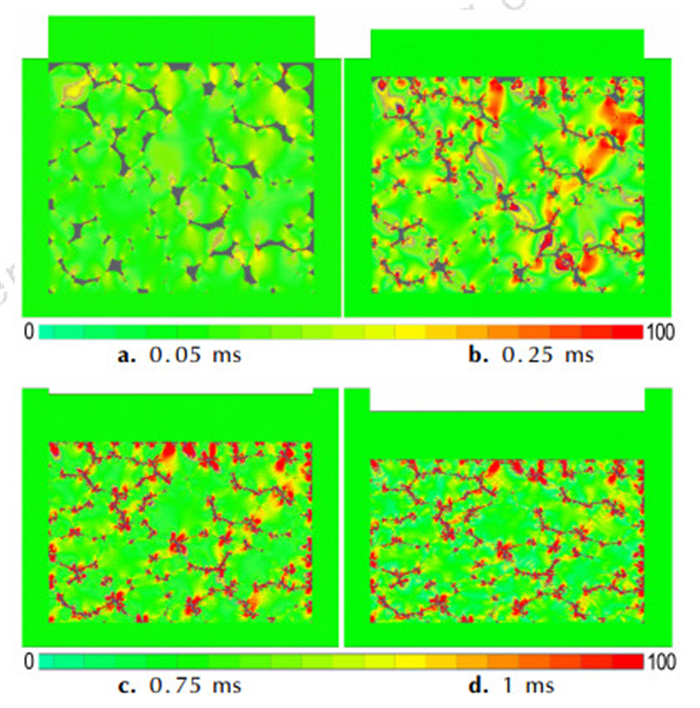
图 4为PBX炸药压制过程中不同时刻应力分布模拟结果。从图 4a和图 4b看出, 在0.25 ms时, 应力沿炸药颗粒间的接触面向刚性模具底板传播, 并形成了多条的应力链。同一个PBX炸药内部应力分布不均匀, 炸药体系顶部处于高应力状态, 底部部分应力较小。应力集中点主要集中在颗粒与刚性压头的接触部分, PBX炸药内部存在应力梯度, 各炸药颗粒之间应力差较大。图 4c和图 4d可以看出炸药体系应力梯度在减小, 这是由于大部分炸药颗粒已发生滑移和变形, 并且处于塑性变形状态。在压缩至1 ms时, 炸药体系已基本处于密实状态, 但各部分应力分布仍然呈不均匀状态。由于在炸药压制成型过程中, 炸药颗粒间所受的压力和摩擦力略大于其他部位, 而导致应力在颗粒接触面较大。从图 4可以看出, 早期阶段炸药体系呈现出一个比较松散的状态, 在不断压缩过程中, 各颗粒之间受到压力开始接触挤压而导致应力变化。这与刘群[14]等利用非线性有限元计算方法模拟JO-9159炸药颗粒压制成型过程得到的结果“应力集中主要出现在药粒与约束面的接触部分; 当药粒之间空隙被填满, 药粒进入塑性变形后, 药粒内部压力迅速升高且压力趋于一致”类似。
|
图 4 PBX炸药压制过程中不同时刻应力分布模拟结果 Fig.4 Stress distribution simulation results of PBX at different times during compression |
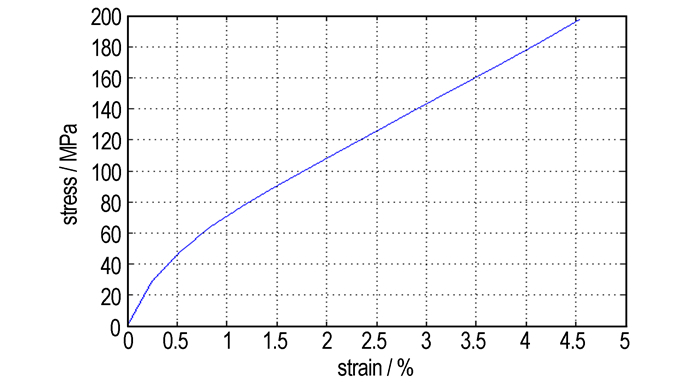
图 5为模拟压制过程中PBX炸药体系整体应力-应变率曲线。图 5表明, 在压缩初始阶段, 应力上升速度较快, 应力和应变呈线性关系, PBX材料表现为弹性性质。超过材料的屈服力后, 受到粘结剂性质影响, PBX材料开始表现为粘性性质, 应力上升速度减缓。上述结论与蔡宣明[15]等关于动态力学响应及细观损伤破坏模式的研究结果“弹性阶段, 应力-应变曲线开始阶段具有较好的线性关系; 屈服阶段, 随着应变的增加, 应力开始减小; 紧接着进入强化阶段, PBX模拟材料抗压能力又开始增强, 应力随着应变的增大而增大”相符。
|
图 5 PBX炸药体系压缩的应力-应变率曲线 Fig.5 Compressive stress-strain rate curve for PBX system |
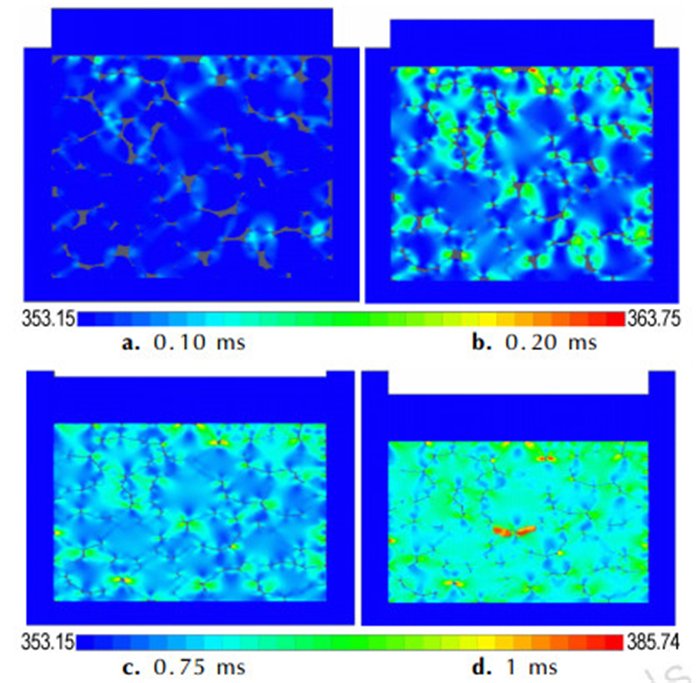
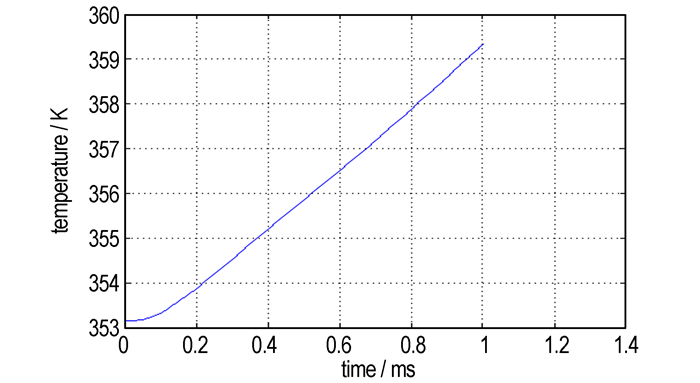
图 6为PBX炸药体系内不同时刻温度分布模拟结果。图 6显示, 炸药体系受压后, 刚性压头与PBX炸药体系接触面温度首先升高, 随着压制的进行, 炸药内部温度逐渐升高, 而达到平衡后, 炸药内部存在温差。从图 6a和图 6b看出, 炸药体系在0.10 ms时, 炸药体系顶部在刚性压头挤压和颗粒间摩擦的作用下温度逐渐升高; 0.25 ms时, 体系内部的局部温度最大上升了10 K。炸药体系底部由于受到压力影响较小, 温度明显低于顶部。图 6c和图 6d可以看出温度变化已经趋于平衡, 表明体系内部温差逐渐减小。在1 ms时, 炸药体系已接近密实状态, 除中心处附近温度较高以外, 其余颗粒温度基本相同, 体系内部最大温差在20 K左右。图 7为模拟过程中, 炸药体系整体温度变化曲线。从图 6、图 7得出, 模拟结束时, 体系整体温度上升到了359.12 K, 局部最高温度为385.74 K。温度变化的模拟结果与文献[16]的结果“PBX炸药在升压过程中均出现内部温度瞬时增高的现象, 达到平衡后, 炸药内部存在温差, 药柱中心处药粒温度最高的结果, 压药柱内部最大温升为29 K”基本一致。
|
图 6 PBX炸药压制过程中不同时刻温度分布模拟结果 Fig.6 Temperature distribution simulation results of PBX at different times during compression |
|
图 7 PBX炸药体系压缩的温度时间变化曲线 Fig.7 Compressive temperature-time curve for PBX system |
采用物质点法, 对HMX基PBX炸药压制过程中的力学行为进行了细观尺度的模拟。在模拟压缩过程中, 刚性压头以0.3 m·s-1的速度从上往下压缩, 模拟时间持续1 ms。模拟结果表明, PBX在压缩的过程中, 位于接触面的炸药颗粒首先受到刚性压头的挤压, 炸药颗粒向下的运动, 颗粒间的缝隙不断减小; 在0.50 ms时, 炸药颗粒已趋于压实的状态; 在0.75 ms时, 炸药颗粒之间均受到不同程度力的挤压, 发生塑性变形, 颗粒轮廓明显改变; 至1 ms时PBX无显著的颗粒特征, 形成密实整体。
结果表明, 压缩中炸药颗粒存在整合和巩固两个阶段。在整合阶段(即0~0.5 ms), PBX颗粒受到压力而重新排列, 应力和温度集中主要出现在炸药颗粒与压缩面的接触部分, 并形成了多条应力链。应力链沿炸药颗粒间的接触面向上和向下传播。炸药体系顶部应力、温度变化均大于底部部分; 当炸药颗粒之间空隙被填满, 炸药体系进入巩固阶段(即0.5~1 ms)。该阶段发生塑性形变, 炸药体系内部炸药体系应力梯度在减小, 炸药颗粒间所受的压力和摩擦力略大于其他部位, 而导致应力在颗粒接触面较大; 在压制过程中, 炸药体系温度升高, 局部温度最大上升了10 K。最后, 炸药体系达到平衡, 内部存在温差, 体系内部最大温差在20 K左右。除中心处附近温度较高以外, 其余颗粒温度基本相同。
本研究中的计算模型和模拟方法同样适用于其他组成的PBX炸药, 在对其它组分的PBX炸药进行模拟时, 只需要输入其相关的物理、化学性质参数。由于计算程序的限制, 本研究中只对HMX基PBX压制过程进行了二维下的数值模拟, 下一步工作是建立HMX基PBX炸药细观结构的三维计算模型, 对炸药压制过程进行三维数值模拟计算。不同压力下、不同颗粒尺径下等多种情况下对应力的传播、变形的影响, 以及炸药颗粒的损伤本构模型的研究有待进一步研究。
| [1] |
Banerjee B, Cady C M, Adams D O. Micromechanics simulations of glass-estane mock polymer bonded explosives[J].
Modelling and Simulation in Materials Science and Engineering, 2003, 11(4): 457 DOI:10.1088/0965-0393/11/4/304 |
| [2] |
兰琼, 唐维, 贺建华, 等. 某HMX基PBX温压时效处理过程变形规律数值模拟[J].
含能材料, 2015, 23(6): 543-547. LAN Qiong, TANG Wei, HE Jian-hua, et al. Simulation on deformation of HMX based PBX by thermal-pressure treatment[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2015, 23(6): 543-547. DOI:10.11943/j.issn.1006-9941.2015.06.007 |
| [3] |
Lusti H R, Gusev A A. Finite element predictions for the thermoelastic properties of nanotube reinforced polymers[J].
Modelling and Simulation in Materials Science and Engineering, 2004, 12(3) |
| [4] |
Menikoff R, Shaw M S. Review of the forest fire model for high explosives[J].
Combustion Theory and Modelling, 2008, 12(3): 569-604. DOI:10.1080/13647830801942402 |
| [5] |
SaeedMoaveni.
Finite element analysis theory and application with ANSYS[M]. Beijing: Publishing House of Electronics Industry, 2012.
|
| [6] |
张涛, 赵北君, 朱世富, 等. PBX粉末成形的数值模拟研究[J].
材料工程, 2009, 35(5): 68-72. ZHANG Tao, ZHAO Bei-jun, ZHU Shi-fu, et al. Numerical simulation study of PBX powder-forming[J]. Journal of Materials Engineering, 2009, 35(5): 68-72. |
| [7] |
Sulsky D, Chen Z, Schreyer H L. A particle method for history-dependent materials[J].
Computer Methods in Applied Mechanics and Engineering, 1994, 118(1): 179-196. |
| [8] |
Hornemann U, Holzwarth A. Shaped charge penetration in alumina targets[J].
International Journal of Impact Engineering, 1997, 20(1): 375-386. |
| [9] |
Andersen S, Andersen L. Analysis of spatial interpolation in the material-point method[J].
Computers & Structures, 2010, 88(7): 506-518. |
| [10] |
Peterson J R, Wight C A, Berzins M. Applying high-performance computing to petascale explosive simulations[J].
Procedia Computer Science, 2013, 18: 2259-2268. DOI:10.1016/j.procs.2013.05.397 |
| [11] |
王晨, 陈朗, 刘群, 等. 多组分PBX炸药细观结构冲击点火数值模拟[J].
爆炸与冲击, 2014, 34(2): 167-173. WANG Chen, CHEN Lang, LIU Qun, et al. Numerical simulation for analyzing shock to ignition of PBXs with different compositions in meso-structural level[J]. Explosion & Shock Waves, 2014, 34(2): 167-173. DOI:10.11883/1001-1455(2014)02-0167-07 |
| [12] |
董海山, 周芬芬.
高能炸药及相关物性能[M]. 北京: 科学出版社, 1989: 334-340.
DONG Hai-shan, ZHOU Fen-fen. High energy explosives and correlative physical properties[M]. Beijing: Science Press, 1989: 334-340. |
| [13] |
Xue L, Borodin O, Smith G D, et al. Micromechanics simulations of the viscoelastic properties of highly filled composites by the material point method (MPM)[J].
Modelling and Simulation in Materials Science and Engineering, 2006, 14(4): 703 DOI:10.1088/0965-0393/14/4/012 |
| [14] |
刘群, 陈朗, 鲁建英, 等. 炸药颗粒压制成型数值模拟[J].
高压物理学报, 2009, 23(6): 421-426. LIU Qun, CHEN Lang, LU Jian-ying, et al. Numerical simulation of explosive particles compaction[J]. Chinese Journal of High Pressure Physics, 2009, 23(6): 421-426. DOI:10.11858/gywlxb.2009.06.004 |
| [15] |
蔡宣明, 张伟, 魏刚, 等. PBX模拟材料动态力学响应及细观损伤模式[J].
含能材料, 2014, 22(5): 658-663. CAI Xuan-ming, ZHANG Wei, WEI Gang, et al. Dynamic mechanics response and mesoscopic damage of a PBX simulant[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2014, 22(5): 658-663. |
| [16] |
贾宪振, 王晓峰, 陈松, 等. 炸药等静压工艺安全性的数值模拟研究[J].
兵工自动化, 2014, 33(7): 65-67. JIA Xian-zhen, WANG Xiao-feng, CHEN Song, et al. Numerical study of safety of explosive isostatic pressing[J]. Ordnance Industry Automation, 2014, 33(7): 65-67. DOI:10.7690/bgzdh.2014.07.018 |
Mechanics behaviors and temperature of PBX in pressing process have been simulated by the material point method.




