石墨烯(GRA)具有优异的结构、物化及力学特性, 在含能材料领域具有广阔的应用前景, 如降低机械感度, 提高热分解稳定性, 增强能量释放效率等[1]。曾有研究表明,功能化的GRA对硝基甲烷(NM)的燃烧反应具有催化作用, 能够提高NM的燃烧速率[2]。随后, 基于第一性原理与反应力场的分子动力学模拟分别揭示出该催化效应的机理源于NM与GRA表面官能团发生的原子交换[3-4]。随着反应温度的增加, GRA也显示出了与功能化GRA相似的催化活性[4]。另外, 量子化学计算结果显示GRA表面能够影响NM三种初始反应活化能的大小, 并改变了活化能的顺序, 也从一定程度上体现了GRA的催化作用[5]。然而, 关于GRA对NM结构排布的影响研究却较少。
密度泛函理论研究结果表明NM分子间相对取向的改变可以引起CN键离解能的变化, 导致NM在不同的外界条件刺激下呈现出不同的敏感程度[6], 这种由结构排布差异所引起的性能变化(如感度、稳定性等)在炸药晶体中表现尤为明显。因此, 在GRA平面结构的诱导下, NM的结构排布很可能与液体状态下的特征不同, 导致分子间的反应传递过程发生变化, 从而影响最终的反应性能。为此, 本研究构建了NM-GRA模型, 借助分子动力学模拟方法从分子尺度上模拟了NM在GRA表面的动力学行为, 通过分析密度分布、偶极矩取向、有序性等, 揭示了NM在GRA表面的结构排布特征, 旨在为基于结构排布差异理解GRA对NM燃烧的催化效应提供一个基本前提。
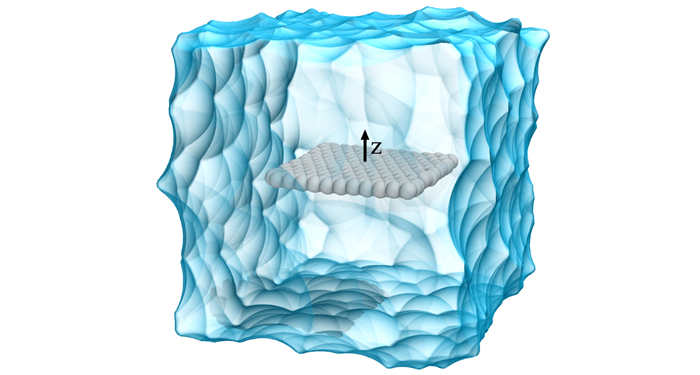
2 计算方法 2.1 结构模型NM溶剂的初始结构取自先前的研究工作[7]。采用CHARMM36分子力场描述NM分子, 该力场能较好地重现出液体NM的密度[8]。通过VMD1.9.1软件[9]中Carbon Nanostructure Builder插件构建单层理想的扶手椅GRA结构, 平面尺寸约为25 Å×25 Å, 并将其法向量沿z轴摆放(见图 1)。采用CHARMM27分子力场[10]中的sp2碳原子参数描述GRA, 原子点电荷设置为0 e。整个模拟体系共包含10351个原子, 对应的模拟盒子尺寸约为51 Å×51 Å×51 Å。为了模拟与数据分析的方便, 借助1.0 kcal/mol/Å2的弱简谐势将GRA限制在初始位置附近。
|
图 1 NM与GRA模拟体系的初始结构 Fig.1 Initial structure of a GRA sheet immersed in liquid NM solvent for the MD simulation |
采用软件NAMD2.9[11]在NPT(等温等压)系综中进行分子动力学模拟, 在笛卡尔坐标系的三维方向上施加周期性边界条件。采用SHAKE/RATTLE方法[12-13]将含有氢原子的共价键长度限制在平衡值。范德华作用的截断半径取12 Å, 长程静电作用由PME算法[14]计算。通过多步Verlet r-RESPA算法[15]对牛顿方程进行积分, 短程作用的积分步长设置为2 fs, 长程作用的积分步长设置为4 fs。借助Langevin动力学和Langevin控压方法[16]将温度和压强分别控制在300 K和105 Pa。体系在最终模拟前经历了如下的平衡步骤: (1) 5000步的能量最小化; (2) 从0 K到300 K的50 ps升温过程; (3) 300 K和1 bar条件下50 ps的平衡过程。然后, 将模拟继续运行10 ns。轨迹分析及可视化由VMD1.9.1软件[9]处理。
3 结果与讨论 3.1 相互作用能为了考察体系在10 ns的模拟时间尺度内是否达到充分平衡, 监测了GRA与NM相互作用能(Einter)随模拟时间的演化情况,其计算公式如式(1):
| $ {E_{{\rm{inter}}}} = {E_{{\rm{total}}}}-{E_{{\rm{GRA}}}}-{E_{{\rm{NM}}}} $ | (1) |
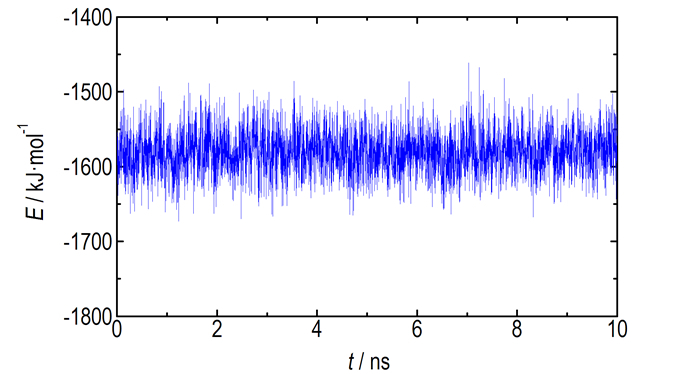
式中, Etotal, EGRA, ENM分别为整个体系、GRA、NM溶剂的势能, kJ·mol-1。GRA与NM相互作用能随模拟时间的演化图如图 2所示,由图 2可知,Einter在整个模拟过程中平稳地波动, 说明10 ns的模拟时间尺度对于NM在GRA表面的结构重排过程是足够的。因此, 选择最后5 ns的模拟轨迹进行后续的数据分析。
|
图 2 GRA与NM相互作用能随模拟时间的演化图 Fig.2 Time evolution of interaction energies between GRA and NM |
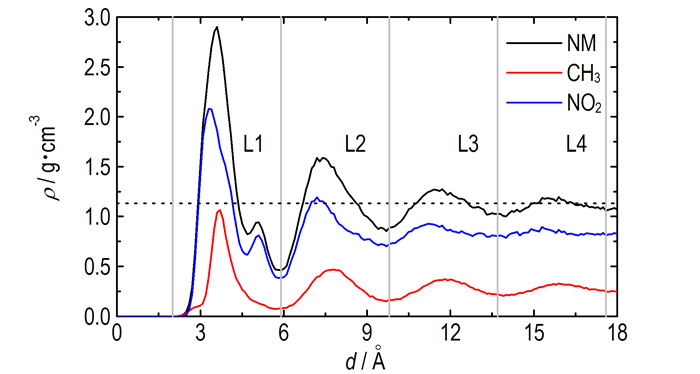
为了考察GRA表面对NM结构排布的影响, 首先统计了NM密度沿GRA平面法向量方向的变化情况, 结果如图 3所示。从图 3可以看出, 随着NM与GRA平面垂直距离的增加, 其密度呈波动式衰减, 最终趋于液体NM的平均密度值。根据峰的位置, 可以将NM沿GRA平面法方向量方向的分布分为4个区域, 分别记为L1(2.0~5.9 Å)、L2(5.9~9.8 Å)、L3(9.8~13.7 Å)和L4(13.7~17.6 Å), 这也说明在GRA平面结构的诱导下, NM呈层状结构分布。其中, L1层内的NM密度最高, 接近3.0 g·cm-3, 约为液体NM平均密度的2.5倍, 说明在GRA范德华作用的驱动下, 大量NM分子聚集在GRA表面。当NM与GRA平面距离增加时, 范德华作用随之减弱, 导致NM密度降低, 从L3层开始, NM密度已逐渐接近平均密度。
|
图 3 NM及其官能团沿GRA平面法向量方向的密度分布图, 黑色虚线为液体NM的平均密度 Fig.3 Mass density profiles of NM, methyl group, and nitro group determined along the normal to the GRA surface as a function of distance. The dash line is the average mass density of bulk NM |
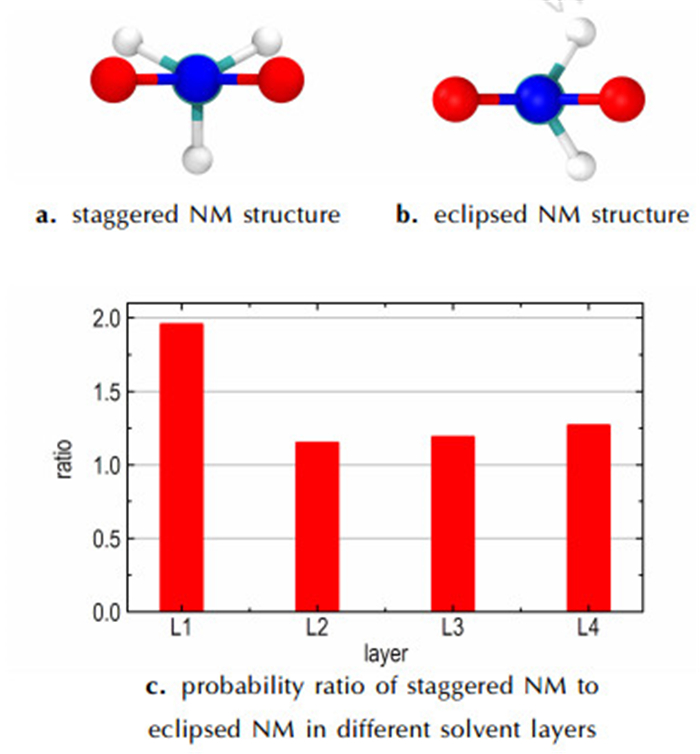
另外,计算了NM中—NO2与—CH3基团的密度分布,结果如图 3所示,由图 3可知,在L1层中,—NO2基团存在两个分布峰,而—CH3基团存在一个分布峰,说明NM分子中—NO2基团相对于—CH3基团存在两种典型的结构取向。由于—NO2和—CH3基团可以绕C—N键进行旋转,导致NM有两种不同的异构体:交错式与重叠式(见图 4),对应的H—C—N—O二面角的最小值分别为30°和0°。在真空中,交错式与重叠式的转化能垒小于0.05 kJ·mol-1,表明—NO2与—CH3基团几乎能够绕着C—N键自由地旋转[17]。在液体NM中,分子动力学模拟结果表明两种结构具有同等的分布概率[7]。然而,当NM在GRA表面时,量化计算显示NM基本保持交错式的结构,此时NM能够最大程度地与GRA平面相互作用[5]。为此,统计了不同层中两种NM构型出现的概率,这里将H—C—N—O二面角的最小值处于0~15°及15~30°的NM结构分别定义为重叠式与交错式。图 4c为不同层中交错式与重叠式结构的概率比。从图 4c可以看出,在L1层内,交错式结构出现的概率约为重叠式结构的2倍,而在其他层中,二者出现的概率基本相等,这与图 3中—NO2与—CH3基团的密度分布是一致的,说明在GRA平面结构的诱导下,部分重叠式结构转化为交错式结构。
|
图 4 NM两种构型及其相对比例 Fig.4 Two structures of MN and their relative ratio |
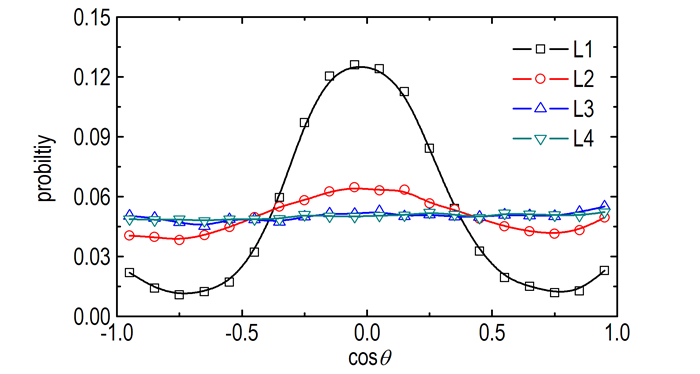
由图 3可知,在GRA表面NM具有很高的局域密度,在如此密集的结构排布中,NM很可能具有某种特定的取向。为了考察NM的排布取向,这里将NM偶极矩矢量与z轴方向的夹角定义为取向角θ (°)。图 5为不同层内NM的cosθ分布图。从图 5中可以看出,在L1层内,取向角在cosθ为0处具有明显的单峰分布,表明NM具有特定的排布取向,即偶极矩矢量平行于GRA平面。在L2层内,NM也具有该特定取向,但分布概率远低于L1层。对于L3和L4层,cosθ分布曲线几乎为一条直线,说明NM已不再具有特定的排布取向,这与液体NM内的分布情况是一致的[7],同时也表明GRA对L3和L4层内NM的结构排布基本没有影响。
|
图 5 不同层内NM的cosθ分布图 Fig.5 Distributions of cosθ for different layers |
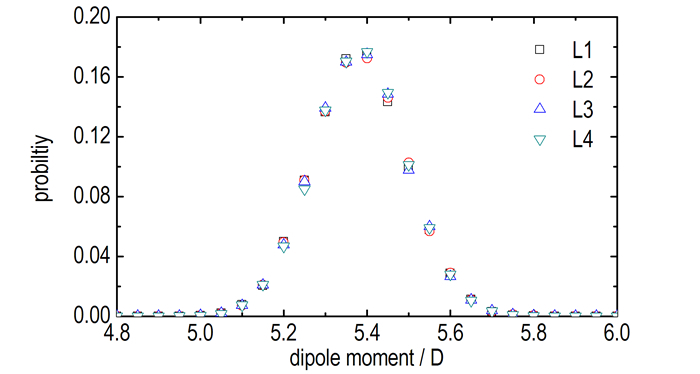
不同层内NM偶极矩大小的分布概率如图 6所示。由图 6可知,所有层内的偶极矩分布情况几乎完全一样,说明GRA平面主要影响了NM的偶极矩取向,并没有改变偶极矩的大小,这可能与GRA中碳原子点电荷为0有关,导致GRA与NM之间不存在静电相互作用,从而难以影响偶极矩的大小。
|
图 6 不同层内NM偶极矩大小的分布图 Fig.6 Distributions of the NM dipole moments for different layers |
图 5也体现了NM结构排布的有序程度,即cosθ分布越集中,则对应的结构排布越有序。因此,采用序参数(S)进一步定量地表示NM结构排布的有序程度[18],其计算公式如式(2):
| $ S = \frac{1}{2}(3{\rm{co}}{{\rm{s}}^2}\theta-1) $ | (2) |
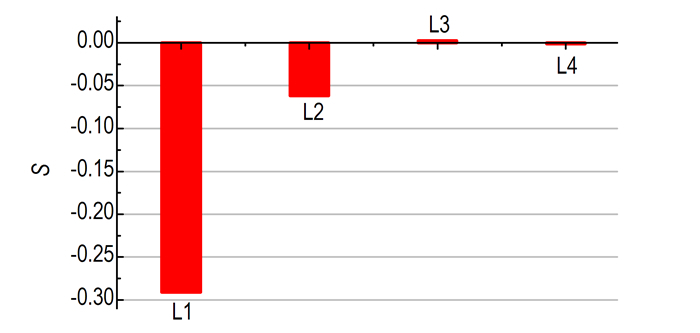
由式(2)可知,当序参数分别为1.0,0.0和-0.5时,NM偶极矩矢量平行、随机及垂直于z轴。图 7为不同层内的平均序参数。从图 7可以看出,L1层的序参数接近-0.5,结构排布的有序程度最高,说明大部分的NM偶极矩矢量垂直于z轴,即平行于GRA表面。相比之下,NM在L2层内的排布也具有一定的有序性,但有序化程度不高。至于L3和L4层,NM的结构排布则不存在有序性,偶极矩矢量的取向完全随机化。因此,GRA表面能够诱导NM进行有序化的结构排布,但随着与GRA表面距离的增加,有序程度逐渐降低。
|
图 7 不同层内NM结构排布的平均序参数 Fig.7 Average order parameter S for different layers |
(1) NM在GRA表面呈层状分布,在L1层内,交错式构型出现的概率约为重叠式构型的2倍,局域密度大于平均密度,结构排布较为密集。
(2) NM在GRA表面呈有序化排布,L1层的有序性最高,NM具有特定的偶极矩取向,即偶极矩矢量平行于GRA平面,但偶极矩的大小并没有改变。
(3) 随着NM与GRA距离的增加,GRA对NM结构排布的影响减弱,L3和L4层基本与液体NM的结构排布一致。
| [1] |
兰元飞, 李霄羽, 罗运军. 石墨烯在含能材料中的应用研究进展[J].
火炸药学报, 2015, 38(1): 1-7. LAN Yuan-fei, LI Xiao-yu, LUO Yun-jun. Research progress on application of grapheme in energetic materials[J]. Chinese Journal of Explosive & Propellants, 2015, 38(1): 1-7. |
| [2] |
Sabourin J L, Dabbs D M, Yetter R A, et al. Functionalized graphene sheet colloids for enhanced fuel/propellant combustion[J].
ACS Nano, 2009, 3(12): 3945-3954. DOI:10.1021/nn901006w |
| [3] |
Liu L M, Car R, Selloni A, et al. Enhanced thermal decomposition of nitromethane on functionalized graphene sheets: ab initio molecular dynamics simulations[J].
Journal of the American Chemical Society, 2012, 134(46): 19011-19016. DOI:10.1021/ja3058277 |
| [4] |
Zhang C Y, Wen Y S, Xue X G. Self-enhanced catalytic activities of functionalized graphene sheets in the combustion of nitromethane: molecular dynamic simulations by molecular reactive force field[J].
ACS Applied Materials & Interfaces, 2014, 6(15): 12235-12244. |
| [5] |
刘英哲, 康莹, 来蔚鹏, 等. 硝基甲烷在石墨烯表面初始反应机理的理论研究[J].
含能材料, 2015, 23(9): 871-876. LIU Ying-zhe, KANG Ying, LAI Wei-peng, et al. Reaction mechanism of nitromethane on the graphene surface: a theoretical study[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2015, 23(9): 871-876. DOI:10.11943/j.issn.1006-9941.2015.09.007 |
| [6] |
Zhang C Y. Stress-induced activation of decomposition of organic explosives: a simple way to understand[J].
Journal of Molecular Modeling, 2013, 19(1): 477-483. |
| [7] |
Liu Y Z, Lai W P, Yu T, et al. Structural characteristics of liquid nitromethane at the nanoscale confinement in carbon nanotubes[J].
Journal of Molecular Modeling, 2014, 20(10): 2459 DOI:10.1007/s00894-014-2459-2 |
| [8] |
Vanommeslaeghe K, Hatcher E, Acharya C, et al. CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields[J].
Journal of Computational Chemistry, 2010, 31(4): 671-690. |
| [9] |
Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics[J].
Journal of Molecular Graphics, 1996, 14(1): 33-38. DOI:10.1016/0263-7855(96)00018-5 |
| [10] |
MacKerell A D, Bashford D, Bellott M, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins[J].
Journal of Physical Chemistry B, 1998, 102(18): 3586-3616. DOI:10.1021/jp973084f |
| [11] |
Phillips J C, Braun R, Wang W, et al. Scalable molecular dynamics with NAMD[J].
Journal of Computational Chemistry, 2005, 26(16): 1781-1802. DOI:10.1002/(ISSN)1096-987X |
| [12] |
Ryckaert J P, Ciccotti G, Berendsen H J C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes[J].
Journal of Computational Physics, 1977, 23(3): 327-341. DOI:10.1016/0021-9991(77)90098-5 |
| [13] |
Andersen H C. Rattle: a "velocity" version of the shake algorithm for molecular dynamics calculations[J].
Journal of Computational Physics, 1983, 52(1): 24-34. |
| [14] |
Darden T, York D, Pedersen L, et al. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems[J].
Journal of Chemical Physics, 1993, 98(12): 10089-10092. DOI:10.1063/1.464397 |
| [15] |
Tuckerman M, Berne B J, Martyna G J. Reversible multiple time scale molecular dynamics[J].
Journal of Chemical Physics, 1992, 97(3): 1990-2001. DOI:10.1063/1.463137 |
| [16] |
Feller S E, Zhang Y, Pastor R W, et al. Constant pressure molecular dynamics simulation: the langevin piston method[J].
Journal of Chemical Physics, 1995, 103(11): 4613-4621. DOI:10.1063/1.470648 |
| [17] |
Megyes T, Bálint S, Grósz T, et al. Structure of liquid nitromethane: comparison of simulation and diffraction studies[J].
Journal of Chemical Physics, 2007, 126(16): 164507 DOI:10.1063/1.2721559 |
| [18] |
Fujiwara S, Sato T. Molecular dynamics simulations of structural formation of a single polymer chain: bond-orientational order and conformational defects[J].
Journal of Chemical Physics, 1997, 107(2): 613-622. DOI:10.1063/1.474421 |

The structural arrangements of nitromethane on the graphene surface were investigated by the analysis of interaction energies, density distribution, dipole orientation, and ordering effect obtained from molecular dynamics simulations.



