近场动力学(PD) 是一种新的基于非局部思想的无网格方法。在分析破坏问题时有限元、有限差分等传统方法会产生裂纹尖端奇异性, 扩展有限元虽然已经解决了很多裂纹扩展和连接问题, 但在分析三维裂纹扩展和群裂纹等复杂破坏问题时面临挑战。无网格法消除了网格依赖性, 但在模拟断裂时遇到了张力不稳定问题。分子动力学方法也被用来模拟裂纹扩展和连接问题, 但存在计算时间长、计算效率低等问题。PD方法兼有分子动力学方法和无网格方法的优点, 避免了传统方法在面临不连续问题时的奇异性, 又突破了分子动力学方法在计算尺度上的缺陷。因此, 该方法在研究损伤、断裂、失稳等问题时具有明显优势。PD方法还有待发展, 传统的粘弹性、塑性以及弹、塑、粘性耦合的材料性质在PD本构模型中的表述尚待深入研究[1-3]。
沥青、混凝土、高聚物、固体推进剂、高聚物粘结炸药等广泛应用于国民经济建设和国防工业中, 在温度和机械载荷的作用下呈现出明显的非线性粘弹性特征, 这类材料力学行为的研究越来越受到重视[4-6]。孟红磊[7]提出了一种含累积损伤的非线性粘弹性本构方程来描述推进剂的拉伸应力-应变关系, 并将其引入有限元分析中获得了较好的计算结果。冯震宇[8]将非线性粘弹性朱-王-唐本构模型应用于飞机风挡的数值模拟, 结果表明本构模型较好地模拟了风挡材料的力学行为。
由于传统数值模拟方法易在损伤处产生奇异, 且具有网格依赖性等缺点, PD方法已开始应用于粘弹性材料的力学行为模拟。Mitchell[9]基于并联形式的Maxwell模型建立了PD线性粘弹性本构模型。Azizi[10]将Burgers模型引入PD键理论, 得到PD线性蠕变本构力函数, 模拟了高分子材料在低应力水平下的线性蠕变, 数值模拟与实验结果较吻合, 但模型本构力函数中的横截面积对于点对相互作用没有明确的物理意义。由于高分子、混凝土、高聚物粘结炸药等材料在高应力作用下呈现出非线性蠕变特性, 模型不能较好地模拟这类材料在温度和应力共同作用下的非线性蠕变行为。
本研究利用Burgers粘弹性模型表征蠕变柔度主曲线, 结合非线性粘弹体的时间-应力等效原理, 得到不同应力水平下蠕变柔度的表达式。将其代入PD本构力函数, 推导出非线性粘弹体的PD蠕变本构力函数, 从而建立起一种可应用于高聚物粘结炸药的近场动力学蠕变模拟方法。利用该方法对PBX9502在不同温度和不同应力作用下的蠕变行为进行模拟, 获得与实验一致的结果。
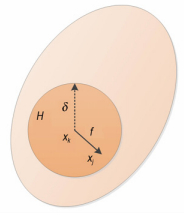
2 PD方法的基本理论 2.1 运动方程PD方法将物体所占区域离散成具有一定质量的物质点, 域内任一物质点xk与其周围一定范围(近场范围H=H(xk, δ)={ xj∈R:‖ xj-xk‖≤δ}) 内的其它物质点xj之间存在相互作用f, 如图 1所示, 也称为本构力函数[11]:
| $\mathit{\boldsymbol{f}} = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{x}}_j},\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{x}}_k},t} \right),\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{x}}_j},t} \right)t} \right)$ | (1) |
|
图 1 物质点与其近场范围内其它物质点的相互作用 Fig.1 Pairwise interaction of a material point with its neighboring points |
根据牛顿第二定律可得物质点xk的运动方程为
| $\rho \left( {{\mathit{\boldsymbol{x}}_k}} \right)\mathit{\boldsymbol{\ddot u}}\left( {{\mathit{\boldsymbol{x}}_k},t} \right) = \int_H {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{x}}_j},\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{x}}_k},t} \right),\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{x}}_j},t} \right),t} \right){\rm{d}}\;{V_j} + \mathit{\boldsymbol{b}}\left( {{\mathit{\boldsymbol{x}}_k},t} \right)} $ | (2) |
式中, ρ为物质点密度, u为物质点的位移, b为单位体积物质所受的外载荷。
2.2 本构力函数的基本形式对于线弹性各向同性材料, Madenci[12]给出了本构力函数f的基本形式
| ${\bf{f}} = cs\frac{{{\mathit{\boldsymbol{y}}_j} - {\mathit{\boldsymbol{y}}_k}}}{{\left| {{\mathit{\boldsymbol{y}}_j} - {\mathit{\boldsymbol{y}}_k}} \right|}}$ | (3) |
式中, yj-yk=xj-xk+ uj-uk; s=(yj-yk -xj-xk)/(xj-xk), 为作用键伸长率; c为与结构尺寸、近场半径和材料柔度相关的参数。令经典理论的应变能密度与PD理论的应变能密度相等, 可分别得到一维、二维和三维情况下c的表达式。
| $c = \left\{ \begin{array}{l} \frac{2}{{A{\delta ^2}J}},\;\;{\rm{one}}\;{\rm{dimension}}\\ \frac{9}{{\pi h{\delta ^3}J}},\;\;{\rm{two}}\;{\rm{dimensions}}\\ \frac{{12}}{{\pi {\delta ^4}J}},\;\;{\rm{three}}\;{\rm{dimensions}} \end{array} \right.$ | (4) |
式中, J为材料柔度, δ为近场半径, h为二维板厚度, A为一维杆的横截面积。
通过改变式(4) 中材料柔度的取值, 可以将线弹性材料的本构力函数扩展到非线性分析。
2.3 方程求解方法PD方法的运动方程式(2) 可离散为
| $\mathit{\boldsymbol{\rho \ddot u}}_k^n = \sum\limits_j {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}_j^n - \mathit{\boldsymbol{u}}_k^n,\mathit{\boldsymbol{x}}_j^n - \mathit{\boldsymbol{x}}_k^n} \right)} \;{V_j} + \mathit{\boldsymbol{b}}_k^n$ | (5) |
其中, n为时间步数。
可见, 近场动力学方法给出的运动方程是动力学形式的, 用它来计算静力学问题时还需做一定的处理, 如可采用引入人工阻尼的动态松弛方法来求解。Underwood[13]提出了一种自适应动态松弛法求解近场动力学运动方程, 其中阻尼随物质点的位移变化, 能较快地使结果收敛。
将式(5) 引入阻尼cn, 并改写成矩阵形式
| ${\mathit{\boldsymbol{\ddot U}}^n}\left( {\mathit{\boldsymbol{x}},{t^n}} \right) + {c^n}{\mathit{\boldsymbol{\dot U}}^n}\left( {\mathit{\boldsymbol{x}},{t^n}} \right) = {\mathit{\boldsymbol{D}}^{ - 1}}{\mathit{\boldsymbol{F}}^n}\left( {{\mathit{\boldsymbol{U}}^n},\mathit{\boldsymbol{U}}{^{'n}},\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}{'}} \right)$ | (6) |
由中心差分法得到
| $\begin{array}{l} {{\mathit{\boldsymbol{\dot U}}}^{n + 1/2}} = \frac{{\left( {2 - {c^n}\Delta t} \right){{\mathit{\boldsymbol{\dot U}}}^{n - 1/2}} + 2\Delta t{\mathit{\boldsymbol{D}}^{ - 1}}{\mathit{\boldsymbol{F}}^n}}}{{\left( {2 + {c^n}\Delta t} \right)}}\\ {\mathit{\boldsymbol{U}}^{n + 1}} = {\mathit{\boldsymbol{U}}^n} + \Delta t{{\mathit{\boldsymbol{\dot U}}}^{n + 1/2}} \end{array}$ | (7) |
初始条件为
| ${\mathit{\boldsymbol{\dot U}}^{1/2}} = \frac{{\Delta t{\mathit{\boldsymbol{D}}^{ - 1}}{\mathit{\boldsymbol{F}}^0}}}{2}$ | (8) |
式中, F为物质点所受合力, D为密度矩阵, 其对角元素满足
| $\begin{array}{*{20}{l}} {{\lambda _{ii}} \ge \frac{1}{4}\Delta {t^2}\sum\limits_j {\left| {{K_{ij}}} \right|} }\\ {\sum\limits_j {\left| {{K_{ij}}} \right|} = \sum\limits_{j = 1}^N {\frac{{\left| {{\xi _{\left( i \right)\left( j \right)}} \cdot \mathit{\boldsymbol{e}}} \right|}}{{\left| {{\xi _{\left( i \right)\left( j \right)}}} \right|}}} \frac{c}{{\left| {{\xi _{\left( i \right)\left( j \right)}}} \right|}}} \end{array}$ | (9) |
式中, e为x, y, z方向的单位矢量, cn为阻尼系数
| ${c^n} = 2\sqrt {\left( {{{\left( {{\mathit{\boldsymbol{U}}^n}} \right)}^{T1}}{\mathit{\boldsymbol{K}}^n}{\mathit{\boldsymbol{U}}^n}} \right)/\left( {{{\left( {{\mathit{\boldsymbol{U}}^n}} \right)}^T}{\mathit{\boldsymbol{U}}^n}} \right)} $ | (10) |
1 Kn为对角刚度系数
| $^1K_{ii}^n = - \left( {F_i^n/{\lambda _{ii}} - F_i^{n - 1}/{\lambda _{ii}}} \right)/\left( {\Delta t\dot u_i^{n - 1/2}} \right)$ | (11) |
动态松弛法是通过添加人工阻尼, 从而求得函数的静态解的一种方法。阻尼越大, 收敛也就越快, 但是人工阻尼的大小不能超过临界阻尼, 否则会造成计算时间过长。
3 非线性粘弹体的PD蠕变本构力函数 3.1 非线性粘弹体的时间-应力等效原理沥青、混凝土、固体推进剂、高聚物以及高聚物粘结炸药等在温度相同的条件下, 应力水平越高, 材料的蠕变应变就越大, 材料呈现出非线性粘弹性特征。此时, 不能只考虑时间和温度, 还需要考虑应力水平对蠕变行为的影响。非线性粘弹体的时间-应力等效原理[14]认为, 材料受载应力水平对蠕变柔度的影响与温度相似, 也具有等效性。依据自由体积理论, 推导出了时间-应力等效原理的表达式[15]:
| $J\left( {\sigma ,t} \right) = {b_\sigma }J\left( {{\sigma _0},t/{a_\sigma }} \right)$ | (12) |
式中, aσ和bσ分别为应力水平和竖直移位因子, 具有与温度移位因子类似的形式, J(σ0, t) 为参考应力σ0下的蠕变柔度主曲线。
3.2 蠕变柔度主曲线的表征粘弹性材料同时具有弹性和粘性特征, 根据流变学理论采用弹性和粘性元件组合描述其粘弹性行为。粘性元件与弹性元件常见的组合模型包括Maxwell模型、Kelvin模型、Burgers模型以及其它复杂模型。一般而言, 材料模型的选择和确定应该遵循以下原则: (1) 模型能够很好地反映材料的力学性能; (2) 模型应尽可能简单、直观。Burgers粘弹性模型是由Maxwell单元和Kelvin单元串联组成的四参数模型, 可以表示高聚物粘结炸药粘弹行为的主要特征[16]。由实验测得的高聚物粘结炸药材料的蠕变曲线与Burgers模型一致性很好。基于以上几点, 本研究选择了Burgers粘弹性模型来描述高聚物粘结炸药的粘弹性行为。
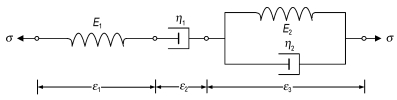
参考应力σ0下的蠕变柔度主曲线可以通过Burgers粘弹性模型来描述, 如图 2所示。
|
图 2 Burgers粘弹性模型 Fig.2 Burgers viscoelastic model |
根据胡克定律和牛顿流体定律可得到, 当应力为常数时Burgers模型的应变表达式为
| $\varepsilon \left( {{\sigma _0},t} \right) = \frac{{{\sigma _0}}}{{{E_1}}} + \frac{{{\sigma _0}t}}{{{\eta _1}}} + \frac{{{\sigma _0}}}{{{E_2}}}\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t}}{{{\eta _2}}}}}} \right)$ | (13) |
式中, E1, E2为弹簧的弹性模量, MPa; η1, η2为粘壶的粘滞系数, MPa; t为时间, s。
令蠕变柔度J(σ0, t)=ε(σ0, t)/σ0, 则:
| $J\left( {{\sigma _0},t} \right) = \frac{1}{{{E_1}}} + \frac{t}{{{\eta _1}}} + \frac{1}{{{E_2}}}\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t}}{{{\eta _2}}}}}} \right)$ | (14) |
由此, 画出Burgers模型的蠕变曲线, 如图 3所示。

|
图 3 Burgers模型的蠕变曲线 Fig.3 Creep curve of Burgers model |
结合式(12) 和式(14) 可以得到不同应力水平下, 非线性粘弹体的蠕变柔度表达式
| $J\left( {\sigma ,t} \right) = {b_\sigma }\left[ {\frac{1}{{{E_1}}} + \frac{{t/{a_\sigma }}}{{{\eta _1}}} + \frac{1}{{{E_2}}}\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t/{a_\sigma }}}{{{\eta _2}}}}}} \right)} \right]$ | (15) |
当时间t为定值时, 材料的蠕变柔度保持不变。因此, 可以将式(15) 代入式(4), 再代入式(3), 得到蠕变各个时刻对应的各参数均具有明确物理意义的PD方法本构力函数
| $f\left( {\sigma ,t} \right) = \left\{ \begin{array}{l} \frac{2}{{A{\delta ^2}}}s\frac{{{y_j} - {y_k}}}{{\left| {{y_j} - {y_k}} \right|}}/{\left\{ b \right._\sigma }\left[ {\frac{1}{{{E_1}}} + \frac{{t/{a_\sigma }}}{{{\eta _1}}} + } \right.\\ \frac{1}{{{E_2}}}\left. {\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t/{a_\sigma }}}{{{\mu _2}}}}}} \right)} \right]\left. {} \right\},\;\;{\rm{one}}\;{\rm{dimension}}\\ \frac{9}{{\pi h{\delta ^3}}}s\frac{{{y_j} - {y_k}}}{{\left| {{y_j} - {y_k}} \right|}}/{\left\{ b \right._\sigma }\left[ {\frac{1}{{{E_1}}} + \frac{{t/{a_\sigma }}}{{{\eta _1}}} + } \right.\\ \frac{1}{{{E_2}}}\left. {\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t/{a_\sigma }}}{{{\mu _2}}}}}} \right)} \right]\left. {} \right\},\;\;{\rm{two}}\;{\rm{dimensions}}\\ \frac{{12}}{{\pi {\delta ^4}}}s\frac{{{y_j} - {y_k}}}{{\left| {{y_j} - {y_k}} \right|}}/{\left\{ b \right._\sigma }\left[ {\frac{1}{{{E_1}}} + \frac{{t/{a_\sigma }}}{{{\eta _1}}} + } \right.\\ \frac{1}{{{E_2}}}\left. {\left( {1 - {{\rm{e}}^{ - \frac{{{E_2}t/{a_\sigma }}}{{{\mu _2}}}}}} \right)} \right]\left. {} \right\},\;\;{\rm{three}}\;{\rm{dimensions}} \end{array} \right.$ | (16) |
利用Fortran自编程序实现算法, 首先将结构离散为均匀分布的物质点, 各个时刻物质点间的相互作用力用式(16) 表示, 采用动态松弛法求得物质点的位移。最后将该方法应用于PBX9502材料的蠕变行为模拟。
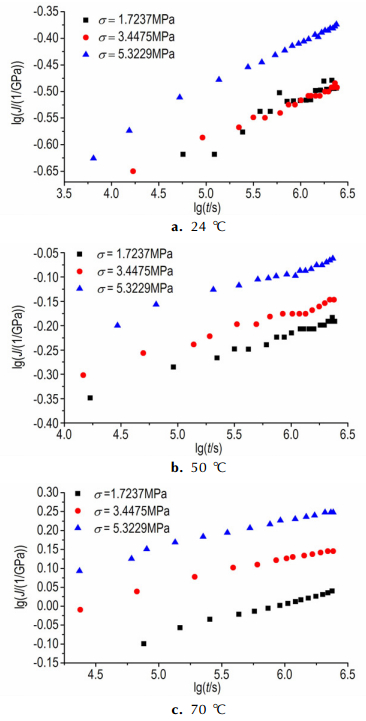
4 应用实例 4.1 应力移位因子的确定Gagliardi [17]针对PBX9502开展了不同温度、不同应力下的圆柱体单轴压缩蠕变实验, 实验结果见图 4。通过公式J=ε/σ, 并取对数, 得到对数蠕变柔度随时间的变化曲线, 如图 5所示。可以看出, 24 ℃时, 1.7237, 3.4475 MPa低应力水平下的蠕变柔度曲线几乎完全重合, PBX9502呈现出了线性粘弹性特性。随着温度的上升, 应力水平越高, 材料的蠕变应变就越大, PBX9502呈现出非线性粘弹性。同时, 不同应力下的蠕变柔度曲线具有相似性, 这与温度变化时的蠕变行为类似, 即时间和应力对PBX9502蠕变行为的影响也具有等效性。

|
图 4 PBX9502的蠕变实验结果 Fig.4 Creep test results of PBX9502 |
|
图 5 不同应力下PBX9502的对数蠕变柔度曲线 Fig.5 Logarithmic creep compliance curves of PBX9502 under different stresses |
以σ0为参考应力, 将其对应的对数蠕变柔度主曲线向其他应力水平下的蠕变曲线做相应的竖直移位, 使两曲线重合, 得到的蠕变曲线如图 6所示。图 6中显示, 经过移位的对数蠕变主曲线与其他应力水平下的蠕变曲线几乎完全重合, 这是由于不同应力下的蠕变柔度曲线具有相似性。因此, 应力水平移位因子aσ=1。

|
图 6 竖直移位后PBX9502的对数蠕变柔度曲线 Fig.6 Logarithmic creep compliance curves of PBX9502 after vertical translation |
另外, 从式(12), 可以看出竖直移位因子bσ等于不同应力下初始柔度的比值。
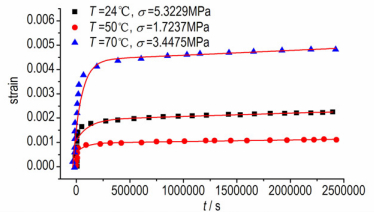
根据如图 4所示的PBX9502的蠕变试验数据, 拟合得到Burgers模型参数, 结果见图 7和表 1。
|
图 7 Burgers模型参数拟合 Fig.7 Parameter fitting of Burgers model |
| 表 1 PBX9502的Burgers模型参数 Tab.1 Parameters of Burgers model for PBX9502 |
通过蠕变柔度主曲线与其他应力水平下蠕变柔度曲线初始柔度的比值, 得到的应力竖直移位因子bσ的取值列于表 2。
| 表 2 应力竖直移位因子bσ的取值 Tab.2 Values of stress vertical translation factor bσ |
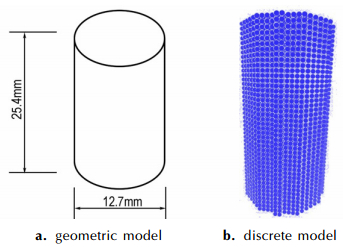
如图 8所示, 蠕变实验采用圆柱体试样[17], 直径12.7 mm, 高25.4 mm, 上下受均匀分布的压应力。模型被离散为均匀的物质点, 计算参数如下: dt=1.0 s, 密度ρ=1900 kg/m3, 泊松比ν=0.25, 物质点间距dx=0.6 mm, 近场半径δ=3dx。
|
图 8 数值计算模型 Fig.8 Numerical simulation model |
|
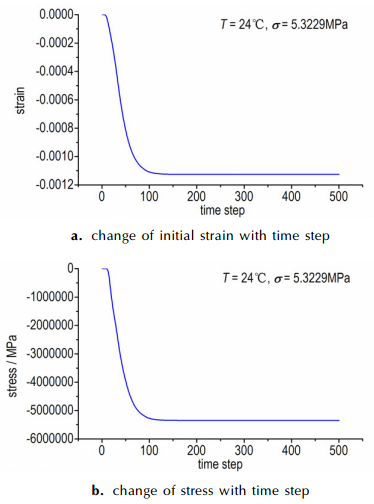
图 9 应力和应变随载荷步的变化 Fig.9 The change of stress and strain with time step |
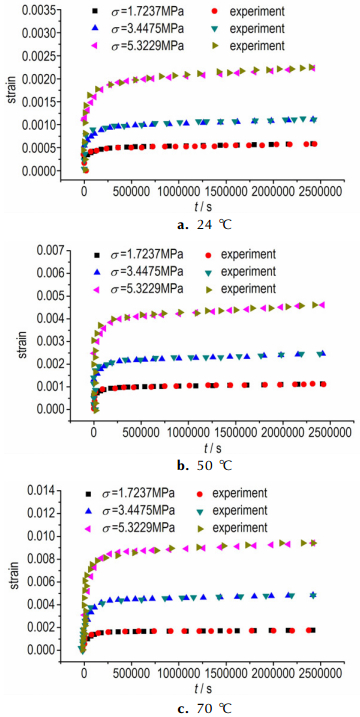
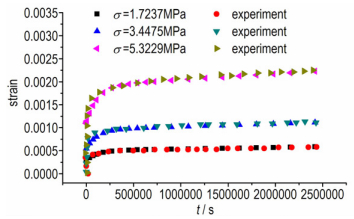
将参考应力σ0对应蠕变柔度主曲线的Burgers模型参数以及应力竖直移位因子bσ代入式(16) 的PD蠕变本构力函数, 得到的模拟蠕变曲线与实验曲线的对比情况见图 10, 可以看出, 模拟曲线与实验曲线吻合很好。
|
图 10 PBX9502模拟蠕变曲线与试验曲线的对比 Fig.10 Comparison of simulated and experimental creep curves of PBX9502 |
近场动力学方法是一种新的无网格方法, 它在分析损伤、断裂和失稳等不连续问题时具有优势。但是, 作为一种新的无网格方法, PD方法还在发展中, 在粘弹性、塑性、损伤断裂与破坏等问题分析上还有待发展, 需要做进一步的研究。
本研究通过非线性粘弹体的时间-应力等效原理, 与Burgers粘弹性模型得到了不同应力作用下材料蠕变柔度的表达式, 推导出非线性粘弹体的PD蠕变本构力函数, 从而建立起可应用于高聚物粘结炸药的近场动力学蠕变模拟方法。模拟了PBX9502在温度和应力作用下的蠕变行为, 获得与实验一致的结果。
本研究建立的近场动力学蠕变行为模拟方法可应用于同时计及温度和应力作用的高聚物粘结炸药的蠕变行为分析。
| [1] |
黄丹, 章青, 乔丕忠, 等. 近场动力学方法以及应用[J].
力学进展, 2010, 40(4): 448-459. HUANG Dan, ZHANG Qing, QIAO Pei-zhong, et al. A review on peridynamics method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448-459. |
| [2] | Gerstle W, Sau N, Silling S A. Peridynamic modeling of concrete structures[J]. Nuclear Engineering and Design, 2007, 237(12-13): 1250-1258. DOI:10.1016/j.nucengdes.2006.10.002 |
| [3] | Kilic B, Agwai A, Madenci E. Peridynamic theory for progressive damage prediction in center-cracked composite laminates[J]. Composite Structures, 2009, 90(2): 141-151. DOI:10.1016/j.compstruct.2009.02.015 |
| [4] |
杨挺青.
粘弹性力学[M]. 武汉: 华中理工大学出版社, 1992: 8-22.
YANG Ting-qing. Viscoelastic mechanics[M]. Wuhan: Press of Huazhong University of Science and Technology, 1992: 8-22. |
| [5] |
周光泉, 刘孝敏.
粘弹性理论[M]. 合肥: 中国科学技术大学出版社, 1996: 8-15.
ZHOU Guang-quan, LIU Xiao-min. Viscoelastic theory[M]. Hefei: Press of University of Science and Technology of China, 1996: 8-15. |
| [6] |
唐明峰, 蓝林钢, 李明, 等. 以RDX为基的浇注PBX力学性能与本构模型[J].
含能材料, 2014, 22(2): 215-220. TANG Ming-feng, LAN Lin-gang, LI Ming, et al. Mechanical properties and constitutive models of RDX based cast PBX[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2014, 22(2): 215-220. |
| [7] |
孟红磊, 鞠玉涛. 含损伤非线性粘弹性本构模型及数值仿真应用[J].
固体火箭技术, 2012, 35(6): 764-768. MENG Hong-lei, JU Yu-tao. Nonlinear viscoelastic equation with cumulative damage and its application on numerical simulation[J]. Journal of Solid Rocket Technology, 2012, 35(6): 764-768. |
| [8] |
冯震宇, 王新军, 王富生, 等. 朱-王-唐非线性粘弹性本构模型在有限元分析中的实现及其应用[J].
材料科学与工程学报, 2007, 25(2): 269-272. FENG Zhen-yu, WANG Xin-jun, WANG Fu-sheng, et al. Implementation and its application in finite element analysis of constitutive model for ZWT nonlinear viscoelastic material[J]. Journal of Materials Science & Engineering, 2007, 25(2): 269-272. |
| [9] | Mitchell J A. A non-local, ordinary-state-based viscoelasticity model for peridynamics. SAND2011-8064, 2011. |
| [10] | Azizi M A, Ariffin A K, Nik M I, et al. The peridynamic model of viscoelastic creep and recovery[J]. Multidiscipline Modeling in Materials and Structures, 2015, 11(4): 579-597. DOI:10.1108/MMMS-03-2015-0017 |
| [11] | Silling S A, Askari E. A meshfree method on the peridynamic model of solid mechanics[J]. Computers and Structures, 2005, 83: 1526-1535. DOI:10.1016/j.compstruc.2004.11.026 |
| [12] | Madenci E, Oterkus E. Peridynamic theory and its applications[M]. New York: Springer Science and Business Media, 2014. |
| [13] | Underwood P. Dynamic relaxation[J]. Comput Meth Trans Anal, 1983, 1: 245-265. |
| [14] | Jazouli S, Wenbo Luo, Bremand F, Vu-Khanh T. Application of time-stress equivalence to nonlinear creep of polycarbonate[J]. Polymer Testing, 2005, 24: 463-467. DOI:10.1016/j.polymertesting.2005.01.002 |
| [15] |
王志方, 张国忠. 胶凝原油蠕变的时间-温度-应力等效性[J].
力学与实践, 2008, 30(1): 62-65. WANG Zhi-fang, ZHANG Guo-zhong. The time-temperature-stress equivalence of creep behavior of gelled crude oil[J]. Mechanics in Engineering, 2008, 30(1): 62-65. |
| [16] |
蔡峨.
粘弹性力学基础[M]. 北京: 北京航空航天出版社, 1989: 54-81.
CAI E. Basis of viscoelastic mechanics[M]. Beijing: Press of Beijing University of Aeronautics and Astronautics, 1989: 54-81. |
| [17] | Gagliardi F J, Cunningham B J. Creep testing plastic-bonded explosives in uni-axial compression[D]. United States: SEM XI international congress Orlando, FL, 2008. |
The expressions of creep compliance under different stresses and the peridynamic creep response functions are deduced combing time-stress equivalence principle of nonlinear viscoelastic materials and utilizing Burgers viscoelastic model. The creep behavior of PBX9502 is simulated.




