在武器系统中, 高聚物粘结炸药(PBX) 部件除了具备固有的爆轰性能外, 常以承受载荷的结构件形式存在。在加工、装配、运输及使用过程中, PBX部件常处于复杂受力状态下, 可能会产生裂纹并有一定的扩展, 从而影响武器系统的可靠性与安全性。
小范围屈服下线弹性断裂力学认为, 裂纹尖端附近应力不可能趋于无穷大, 在裂纹尖端核心区域存在一定的屈服区。屈服区内材料发生屈服失效, 屈服区外材料依然满足线弹性断裂力学理论[1]。本文研究的PBX材料拉伸过程没有明显的屈服阶段, 而裂纹尖端附近应力又不可能趋于无穷大, 因此认为裂纹尖端存在相对更小的失效破坏区域。在失效区内PBX材料发生力学失效, 失效区外材料依然满足线弹性断裂力学理论。美国阿拉莫斯实验室的Liu C等[2-3]对PBX-9501和PBX-9502裂纹长期研究发现, 裂纹尖端附近存在较大的损伤区域(Damage Zone)。根据其关于裂纹尖端区域应变场的监测, 以及PBX-9502拉伸破坏应变(0.3%左右), 可以估计出PBX-9502裂纹尖端损伤区尺寸大约为3 mm。PBX-9502材料力学性能体现出较软的特点, 在其损伤区边界附近区域材料仍保有力学性能, 中心区域则出现材料力学失效, 即本文研究的裂纹尖端失效区。美国空军实验室Liu C T[4-5]对另外一种颗粒填充复合含能材料(固体推进剂) 的裂纹研究也发现, 推进剂材料有相对更加明显的塑形力学特性, 其裂纹尖端区域塑性屈服区域非常明显。因此, PBX裂纹尖端失效区的理论研究具有一定的工程应用价值, 有助于更加深入认识PBX裂纹尖端附近核心区域特征。
PBX作为一类以高聚物粘接剂为连续相、高能炸药颗粒为分散相的非均质颗粒高体积填充的复合材料, 由于炸药晶粒、粘接剂和炸药-粘接剂界面的强度互不相同, 因此PBX力学行为表现出拉压不对称的特性[6]。由于粘接剂材料力学性能受温度影响非常大, 在不同温度区间, PBX力学性能也有很大差异[7]。因此, PBX裂纹尖端失效区研究一定要充分考虑材料拉压比和温度的影响。
根据断裂力学理论, PBX裂纹尖端失效区计算准确与否依赖于强度准则的选取。唐维等[8-9]基于单轴加载技术, 从实验和数值模拟两个方面, 对比分析四种常用强度准则在炸药强度分析中的适用性。从描述精度来看, Mohr-Coulomb准则最优, Twin-shear和Drucker-Prager准则次之, 最大正应力准则由于不能体现出出材料拉压比的特点描述精度最差。王鹏飞等[10]在对PBX厚壁结构件热应力破坏研究中, 对几种常用强度准则对比分析发现, Drucker-Prager准则综合考虑了拉压比、平均应力和偏应力对材料强度的影响。Drucker-Prager准则更适合于PBX炸药强度分析, 能描述PBX双轴拉伸强度比单轴拉伸强度略低的现象。
本研究基于Mohr-Coulomb、Twin-shear和Drucker-Prager三种强度准则, 计算了PBXⅠ型裂纹裂尖失效区。根据三种强度准则本身特点, 分析其在PBX裂纹尖端失效区计算中的适用性。利用Drucker-Prager准则的优点, 研究材料拉压比和温度对PBXⅠ型裂纹尖端失效区大小的影响。
2 强度准则PBX材料具有明显的拉压强度不相等特性, 本文选取已经应用于PBX破坏失效分析中的强度准则, 即Mohr-Coulomb准则、Twin-shear准则和Drucker-Prager准则。表达式分别如下[8]:
| ${\sigma _1} - \alpha {\sigma _3} = {\sigma _{\rm{t}}}$ | (1) |
| ${\sigma _1} - \frac{\alpha }{2}\left( {{\sigma _2} + {\sigma _3}} \right) = {\sigma _{\rm{t}}}\;\;\;\;{\sigma _2} \le \frac{{{\sigma _1} + \alpha {\sigma _3}}}{{1 + \alpha }}$ | (2a) |
| $\frac{1}{2}\left( {{\sigma _1} + {\sigma _2}} \right) - \alpha {\sigma _3}{\rm{ = }}{\sigma _{\rm{t}}}\;\;\;\;{\sigma _2} \ge \frac{{{\sigma _1} + \alpha {\sigma _3}}}{{1 + \alpha }}$ | (2b) |
| $\left\{ \begin{array}{l} {\tau _8} + \frac{{\sqrt 2 \left( {1 - \alpha } \right)}}{{\left( {1 + \alpha } \right)}}\;{\sigma _8} = \frac{{2\sqrt 2 {\sigma _{\rm{t}}}}}{{3 + \left( {1 + \alpha } \right)}}\\ {\tau _8}{\rm{ = }}\frac{1}{3}\sqrt {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _1}} \right)}^2}} \\ {\sigma _8}{\rm{ = }}\frac{1}{3}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right) \end{array} \right.$ | (3) |
式中, σ1、σ2和σ3分别为第一、第二和第三主应力。材料破坏强度拉压比为
平面应力状态下, Ⅰ型裂纹尖端区域主应力场为[1]:
| $\left\{ \begin{array}{l} {\sigma _1}{\rm{ = }}\frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}} \right)\\ {\sigma _2}{\rm{ = }}\frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}} \right)\\ {\sigma _3} = 0 \end{array} \right.$ | (4) |
式中, r、θ为裂纹尖端附近点的极坐标, KI为Ⅰ型裂纹应力强度因子。
平面应变状态, Ⅰ型裂纹尖端区域主应力场为[1]:
当0≤θ < 2arcsin (1-2ν) 时
| $\left\{ \begin{array}{l} {\sigma _1}{\rm{ = }}\frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}} \right)\\ {\sigma _2}{\rm{ = }}\frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}} \right)\\ {\sigma _3} = \frac{{2\nu {K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2} \end{array} \right.$ | (5a) |
当2arcsin (1-2ν)≤θ < π时
| $\left\{ \begin{array}{l} {\sigma _1}{\rm{ = }}\frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}} \right)\\ {\sigma _2}{\rm{ = }}\frac{{2\nu {K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\\ {\sigma _3} = \frac{{{K_{\rm{I}}}}}{{\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}} \right) \end{array} \right.$ | (5b) |
式中, ν为材料泊松比。
3.2 Mohr-Coulomb准则失效区对于平面应力, 将式(4) 代入式(1) 可推出裂纹尖端失效区矢径为:
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {1 + \sin \frac{\theta }{2}} \right]^2}$ | (6) |
对于平面应变, 当0≤θ < 2arcsin (1-2ν) 时, 将式(5a) 代入式(1) 可推出裂纹尖端失效区失径为:
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left( {1 - 2\alpha \nu + \sin \frac{\theta }{2}} \right)^2}$ | (7a) |
当2arcsin (1-2ν)≤θ < π时, 将式(5b) 代入式(1) 可推出裂纹尖端失效区失径为:
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {1 - \alpha + \left( {1 + \alpha } \right)\sin \frac{\theta }{2}} \right]^2}$ | (7b) |
对于平面应力, 当
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}$ | (8a) |
当
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {1 - \frac{\alpha }{2} + \left( {1 + \frac{\alpha }{2}} \right)\sin \frac{\theta }{2}} \right]^2}$ | (8b) |
对于平面应变问题, 当
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {1 - 2\alpha \nu } \right]^2}$ | (9a) |
当
| $r = \frac{{K_{\rm{I}}^2}}{{2\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {1 - \frac{\alpha }{2} - \alpha \nu + \left( {1 + \frac{\alpha }{2}} \right)\sin \frac{\theta }{2}} \right]^2}$ | (9b) |
当
对于平面应力, 将式(4) 代入式(3) 可推出裂纹尖端失效区失径为:
| $r = \frac{{K_{\rm{I}}^2{{\left( {1 + \alpha } \right)}^8}}}{{8\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {\frac{{2\left( {1 - \alpha } \right)}}{{1 + \alpha }} + \sqrt {1 + 3{{\sin }^2}\frac{\theta }{2}} } \right]^2}$ | (10) |
对于平面应变, 将式(5a) 或(5b) 代入式(3) 可推出裂纹尖端失效区失径为:
| $r = \frac{{K_{\rm{I}}^2{{\left( {1 + \alpha } \right)}^8}}}{{8\pi \sigma _{\rm{t}}^2}}{\cos ^2}\frac{\theta }{2}{\left[ {\frac{{2\left( {1 + \nu } \right)\left( {1 - \alpha } \right)}}{{1 + \alpha }} + \sqrt {{{\left( {1 - 2\nu } \right)}^2} + 3{{\sin }^2}\frac{\theta }{2}} } \right]^2}$ | (11) |
当材料拉压比α=1时, 式(10) 和(11) 退化为Von-Mises准则裂纹尖端失效区矢径。
对于Ⅰ型裂纹, 其裂纹失效区具有关于裂纹面对称的特点, 因此只需求出0~180°的失径, 180°~360°失径根据对称性可作出。
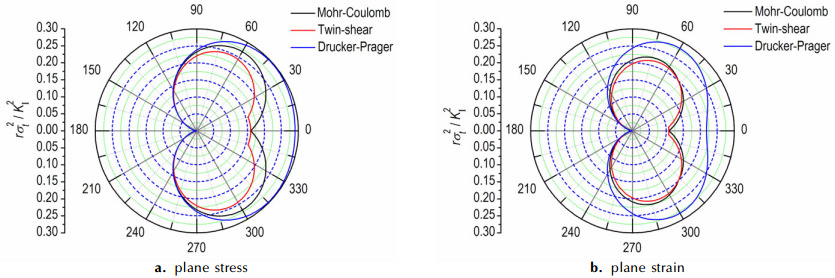
4 结果与讨论 4.1 三种强度准则适用性基于Mohr-Coulomb、Twin-shear和Drucker-Prager三种强度准则计算的PBXⅠ型裂纹尖端失效区如图 1所示。Mohr-Coulomb准则比Twin-shear准则计算的裂尖失效区相对更大一些, 平面应力下这个差别更加明显。Drucker-Prager准则在考虑材料拉压比的基础上, 综合考虑了平均应力和偏应力的影响, 计算的裂尖失效区相对最大, 认为Drucker-Prager准则相对更适合PBX裂尖失效区的计算。比较图 1a和图 1b可以看出, 平面应力比平面应变下Ⅰ型裂纹尖端失效区相对更大。
|
图 1 不同强度准则下PBX Ⅰ型裂纹尖端失效区(α=0.3, ν=0.3) Fig.1 PBX modeⅠcrack tip failure zone based on different strength criterion |
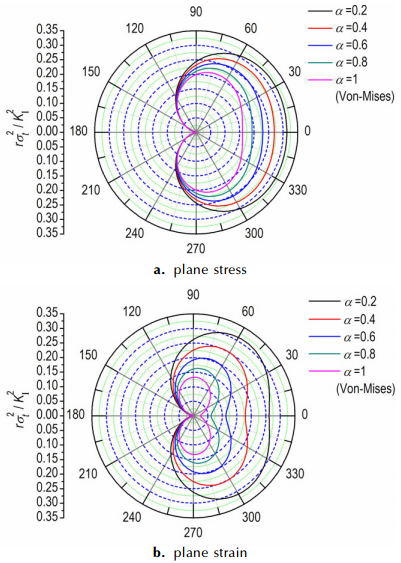
为了研究材料拉压比对裂纹尖端失效区的影响, 利用Drucker-Prager计算了不同拉压比下裂纹尖端失效区, 如图 2所示。PBX材料拉压比约为0.3左右。
|
图 2 材料拉压比对裂纹尖端失效区的影响 Fig.2 Effects of tension-compression strength ratio of the material on the crack tip failure zone |
图 2给出了不同拉压比下, PBX裂纹尖端失效区大小。
材料拉压比对裂纹尖端失效区有着非常大的影响, 随着拉压比的减小, 失效区尺寸显著增大, 平面应变情形下这种增大趋势更加明显。比较图 2a和图 2b, 平面应变比平面应力失效区相对较小, 特别是在|θ|较小区域, 这种现象更加显著。
表 1给出当θ=0°时, PBXⅠ型裂纹尖端失效区无量纲失径rσt2/KI2。表中数据可见, 随着材料拉压比的减小, 平面应变和平面应力下裂纹尖端失效区失径比明显增大。说明不断减小的拉压比对平面应变下失效区的影响更大。
| 表 1 θ=0°时裂纹尖端失效区无量纲矢径 Tab.1 Dimensionless radius vector of crack tip failure zone at θ=0° |
本研究以TATB基某PBX为例, 基于Drucker-Prager强度准则, 在不同温度下, 计算平面应变下该炸药Ⅰ型裂纹尖端极限失效区。借鉴混凝土结构裂纹尖端塑性屈服区计算的材料参数选取[11], 计算所需的相关材料参数见表 2。由于该型PBX的粘结剂玻璃化温度较低, 其高温条件下的断裂韧性和拉伸压缩强度均明显降低。
| 表 2 PBX断裂及力学性能参数[12] Tab.2 Fracture and mechanics properties parameters of PBX |
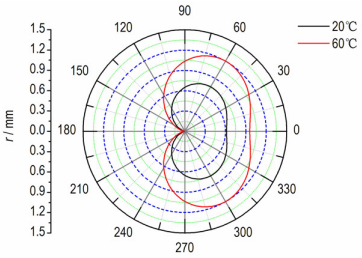
图 3给出了该PBX平面应变Ⅰ型裂纹尖端极限失效区区域。由图 3可见, 当θ=0°时, 常温20 ℃下, 该PBX裂纹尖端失效区失径约为0.61 mm。高温60 ℃下, 失效区失径约为0.95 mm, 失径显著增大, 这是粘接剂超过其玻璃化温度(Tg=35~55 ℃)[12], 材料发生软化导致的。
|
图 3 不同温度下PBXⅠ型裂纹尖端极限失效区(平面应变) Fig.3 PBX mode Ⅰ crack tip ultimate failure zone at different temperature (plane strain) |
基于几种常用于PBX破坏分析的强度准则, 计算了Ⅰ型裂纹尖端失效区, 给出了反应材料拉压比性能差异的裂纹尖端失效区失径表达式。获得了以下结论:
(1) 基于不同强度准则计算的PBX裂纹尖端失效区差别很大, 选取适合PBX材料的强度准则非常重要。Drucker-Prager强度准则综合考虑了材料拉压比、平均应力及偏应力等因素, 计算的裂纹尖端失效区相对最大, 认为该准则更适合PBX裂纹尖端失效区求解。研究发现, 平面应力下比平面应变下裂纹尖端失效区相对更大。
(2) 材料拉压比对于裂纹尖端失效区影响非常大, 随着拉压比的减小, 裂纹尖端失效区明显增大。PBX属于典型的拉伸和压缩力学性能不对称的复合材料, 其裂纹尖端失效区计算需要充分考虑材料拉压比的影响。
(3) PBX材料断裂和力学性能参数受温度影响非常大。基于Drucker-Prager强度准则, 当θ=0时, 20 ℃下的裂纹尖端极限失效区失径为0.61 mm; 60 ℃下PBX裂纹尖端极限失效区失径为0.95 mm。裂纹尖端极限失效区在高温60 ℃下显著增大。
| [1] |
程靳, 赵树山.
断裂力学[M]. 北京: 科学出版社, 2006: 24-29.
CHENG Jin, ZHAO Shu-shan. Fracture mechanics[M]. Beijing: Science press, 2006: 24-29. |
| [2] | Liu C. Fracture ofthe PBX 9501 high explosive[C]//Shock Compression of Condensed Matter, American Institute of Physics, 2003: 786-791. |
| [3] | Liu C, Thompson D G. Crack initiation and growth in PBX 9502 high explosive subject to compression[J]. Journal of Applied Mechanics, 2014, 81(101004): 1-13. |
| [4] | Liu C T. Crack growth behavior in a solid propellant[J]. Engineering Fracture Mechanic, 1997, 56(1): 127-135. DOI:10.1016/S0013-7944(96)00107-5 |
| [5] | Liu C T, Tam M. Investigating the effects of pressure on the near tip behavior and crack growth in a particulate composite material[C]//Fatigue Damage of Materials: Experiment and Analysis, 2003: 243-251. |
| [6] | Belmas R, Reynier P. Mechanical behavior of pressed explosives[C]//International Symposium Energetic Materials Technology, 1994: 360-365. |
| [7] | Rae P J, Parker G R, Dickson P M. The high temperature stress/strain and stress relaxation response of unconfined PBX 9501 between 21 and 210 ℃[C]//14th International Detonation Symposium, 2010: 677-683. |
| [8] |
唐维, 李明, 温茂萍, 等. 四种强度准则在高聚物粘结炸药强度分析中的适应性[J].
固体力学学报, 2013, 34(6): 550-556. TANG Wei, LI Ming, WEN Mao-ping, et al. Adaptability of four strength criterions in polymer bonded explosives strength analysis[J]. Chinese Journal of Solid Mechanic, 2013, 34(6): 550-556. |
| [9] |
唐维, 颜熹琳, 李明, 等. 基于间接三轴拉伸破坏试验的某TATB基PBX强度准则适应性分析[J].
含能材料, 2015, 23(6): 532-536. TANG Wei, YAN Xi-lin, LI Ming, et al. Adaptability analysis of strength criterion on TATB based PBX by indirect triaxial tensile collapse test[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2015, 23(6): 532-536. |
| [10] |
王鹏飞, 黄西成, 何颖波, 等. 热弹性环境下HMX基PBX厚壁结构件失效破坏分析[J].
含能材料, 2016, 24(2): 129-136. WANG Peng-fei, HUANG Xi-cheng, HE Ying-bo, et al. Failure damage analysis of HMX based PBX thick wall structure under thermoelastic environment[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2016, 24(2): 129-136. |
| [11] |
赵均海, 魏雪英, 马淑芳. 混凝土结构Ⅰ型裂纹裂尖塑性区研究[J].
工程力学, 2006, 23(9): 141-145. ZHAO Jun-hai, WEI Xue-ying, MA Shu-fang. Crack tip plastic zone of typeI crack for concrete structure[J]. Engineering Mechanics, 2006, 23(9): 141-145. |
| [12] |
温茂萍, 庞海燕, 田勇, 等. PBX平面应变断裂韧度随温度的变化规律[J].
火炸药学报, 2005, 28(3): 63-65. WEN Mao-ping, PANG Hai-yan, TIAN Yong, et al. Regulations of plane strain fracture toughness of PBX changed with temperatures[J]. Chinese Journal of explosives & Propellant, 2005, 28(3): 63-65. |
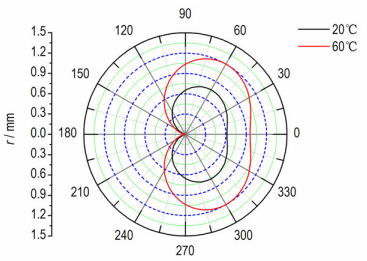
PBX modeⅠ crack tip failure zone was calculated based on Mohr-Coulomb, Twin-shear or Drucker-Prager strength criterion. The influences of tension-compression strength ratio and temperature on the crack tip failure zone were studied.




