多孔硝基胍(NGu) 发射药不仅具有良好的燃面渐增性, 而且具有能量高、烧蚀率低、炮口烟焰较少等特点, 已广泛应用于大口径火炮武器中。弹道性能的一致性主要取决于发射药成型尺寸(如内、外弧厚, 孔径) 和加工质量。目前我国硝基胍发射药制造以压伸成型为主, 生产过程可能造成发射药药柱偏孔、表面粗糙甚至裂纹等现象[1], 制出的成型发射药弧厚不均匀, 孔径不一致, 尺寸波动较大, 无法满足火炮精确装药设计, 严重影响火炮性能的发挥甚至还可能出现炸膛危险。长期以来由于受发射药流动规律以及工艺难以精确控制的限制, 制备合格形状尺寸发射药主要依赖于反复试验以及操作者自身经验, 成本高、效率低, 即使成熟产品在不同季节也需要根据实验确定不同工艺条件。
为实现对发射药等含能材料精密化制造, 采用数值仿真方法[2-5]高效解决含能材料加工工艺问题的仿真研究逐成为一种趋势。针对推进剂在螺杆挤出过程中容易引起爆炸安全性问题, Yang K[6]、Zhou Ke[7]、钟婷婷[8]、霍朝沛[9]等分别利用数值仿真方法分析了不同螺杆参数对单、双螺杆挤出推进剂过程中安全性的影响; 并且分析了药料自身性质对推进剂单螺杆挤出过程中的影响。针对螺杆挤出工艺参数对连续式制备变燃速发射药流动过程的问题, 刘林林[10]通过有限元计算方法分析了不同螺杆转速和入口压力对体积速率的影响规律; 张丹丹[11]模拟定性分析挤出过程中药料体积流量、温度、溶剂比等工艺参数对模具内压力分布以及出口处速度的影响。由于硝基胍发射药工艺复杂, 运用数值仿真的方法研究硝基胍发射药工艺仍处于初步探索阶段, 仿真精度尚未能满足工程实际需求。
针对硝基胍发射药配方和压伸工艺对成型尺寸的影响因素, 利用有限元方法建立硝基胍发射药压伸过程数学模型, 研究硝基胍发射药配方对压伸过程的压力场、速度场以及剪切速率场的影响, 并结合实验压伸发射药尺寸进行验证。
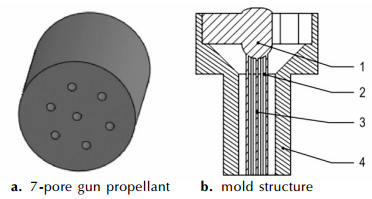
2 有限元分析 2.1 基本假设7孔硝基胍发射药形状以及发射药模具结构示意图如图 1。模具包括模体、模针、针架、针套四个部分, 结构较为复杂, 模针细(0.6 mm) 且数量较多, 尺寸参数较小(针间距1.65 mm), 并且发射药药料粘度较大, 流动过程容易对模针造成挤压产生偏孔等现象, 严重影响发射药加工质量。为提高药料压伸仿真过程准确性, 做出以下假设:
|
图 1 七孔发射药和模具结构示意图 1—针架, 2—针套, 3—模针, 4—模体 Fig.1 Schematic diagrams of 7-pore gun propellant and mold structure 1—needle holder, 2—needle cover, 3—needle, 4—mold |
(1) 发射药为不可压缩的高粘性非牛顿流体。
(2) 发射药在药模中流速较慢, 而且采用恒温药缸对模具保温, 药料为等温流动。
(3) 由于雷诺数较小, 发射药为三维稳态层流流动, 发射药粘性力对流场影响远远大于重力, 故重力可忽略。
(4) 发射药模具尺寸较小, 压伸过程开始有预保压工序, 压伸中药料充满整个模具中。
2.2 控制方程根据发射药在模具内流动特点, 建立硝基胍发射药压伸过程, 药料流动方程如下:
发射药药料连续性方程:
| $ \nabla v = 0 $ | (1) |
发射药药料流动动量方程:
| $ - \nabla pI + \nabla \tau = 0 $ | (2) |
硝基胍发射药药料流变规律受温度、配方以及溶剂含量变化影响较大, 选取Power本构模型描述硝基胍发射药的流变过程, 其表达式如下:
| $ \eta = K{\left( {\lambda \dot \gamma } \right)^{n - 1}} $ | (3) |
式中, η为表观粘度, Pa·s; γ为剪切速率, s-1; v为体积速度, m3·s-1; p为压力差, Pa; I为单位张量; τ为应力张量; ▽为哈密顿算子; K为粘度系数; λ为松弛时间, s; n为非牛顿指数。
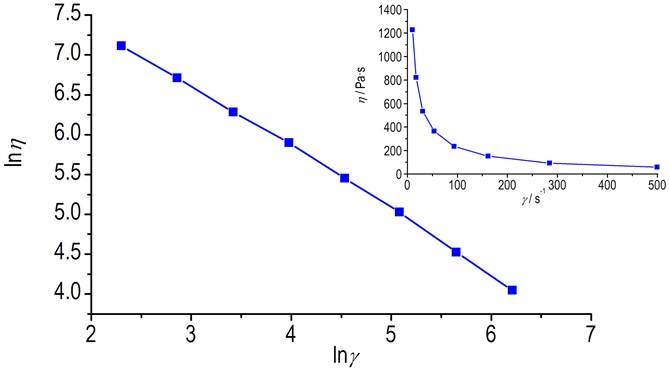
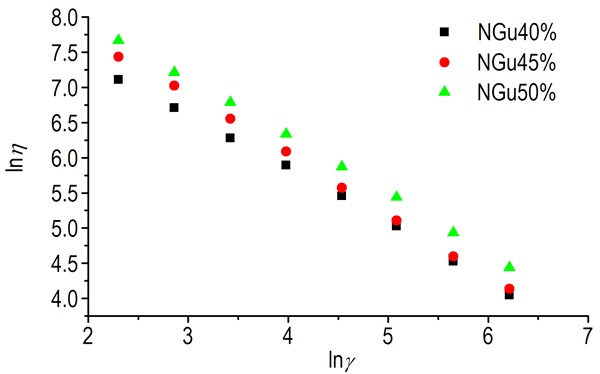
通过RH-2000型毛细流变仪分别测定表 1所示三种配方的塑化药料流变曲线。35 ℃时配方2流变数据如表 2所示。图 2为配方2的流变曲线, 其它流变曲线见图 3。由图可知, 三种不同硝基胍配方发射药表观粘度与剪切速率双对数曲线表现出良好的线性关系。三种配方硝基胍发射药在流动过程中表现出假塑性流体的特征, 不同配方硝基胍发射药流变数据拟合参数结果如表 3。
| 表 1 硝基胍发射药配方 Tab.1 Formulations of NGu gun propellant |
| 表 2 35 ℃时配方2流变数据 Tab.2 Rheological data of formulation 2# at 35 ℃ |
|
图 2 35 ℃时配方2的流变曲线 Fig.2 The rheological curves of formulation 2# at 35 ℃ |
|
图 3 35 ℃时不同配方的流变曲线 Fig.3 The rheological curves of different formulations at 35 ℃ |
| 表 3 药料流变数据Power模型拟合结果 Tab.3 The results of fitting the rheological data of propellant slurry with Power model |
以7孔发射药模具为对象, 根据表 4所示内流道参数建立内流道物理模型和网格模型。
| 表 4 七孔发射药内流道参数 Tab.4 Inner flow channel structure parameters of the 7-pore gun propellant |
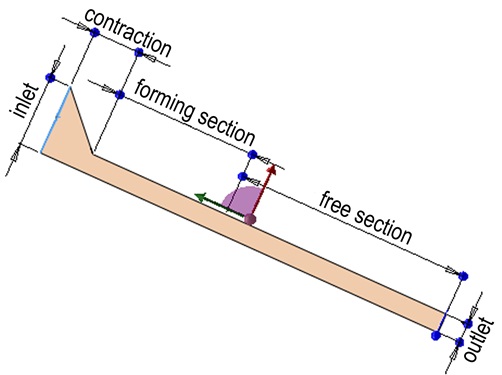
由于七孔药模流道为高度对称几何体, 因此取内流道的1/6部分进行仿真计算, 如图 4所示。针对收缩段结构复杂, 采用Tetrahedron划分方法对收缩段进行划分, 有利于网格细化; 成型段和自由段截面形状一致, 为保证求解精度同时减少网格数目, 采用sweep方法扫掠生成六面体网格; 由于收缩段与自由段交界部分可能出现非稳态流动, 采用局部网格细化的方法, 实现网格平滑过渡以保证求解结果的收敛性, 网格模型如图 5所示。
|
图 4 7孔发射药药模具流道结构 Fig.4 Flow channel structure of 7-pore gun propellant mold |

|
图 5 7孔发射药药模具网格模型 Fig.5 Mesh model of 7-pore gun propellant mold |
根据发射药实际压伸过程, 恒温药缸为35 ℃, 入口流量(inlet) 控制在3×10-7 m3·s-1左右, 取实际压伸体积流量1/6作为仿真入口流量, 即入口体积流量5×10-8 m3·s-1。出口处(outlet) 法向应力和切向速度均为0, 其它边界条件如表 5。
| 表 5 流动边界条件 Tab.5 Flow boundary conditions |
由于发射药压伸流动为多维非线性过程, 为保证求解结果良好的收敛性, 粘度采用Picard迭代算法, 能够将多维问题转换成平面问题且收敛结果满足精度要求; 速度采用Quadratic迭代, 压力采用linear计算方法, 不仅能够够保证求解精度而且能提高求解速度, 收敛步设定为30, 收敛精度设定为0.0001。
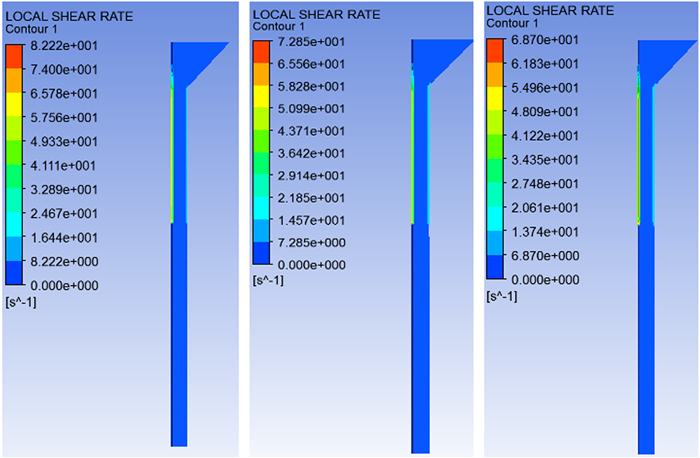
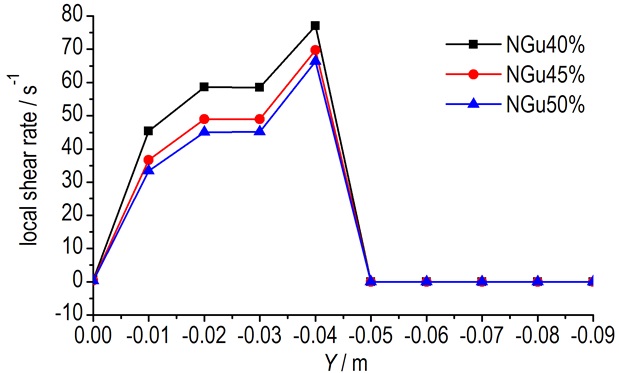
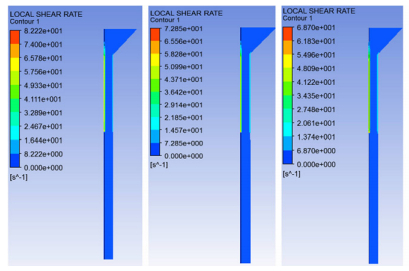
3 仿真结果及分析 3.1 硝基胍发射药配方对剪切速率的影响体积流量5×10-8 m3·s-1, 温度为35 ℃, 配方1, 2, 3的硝基胍发射药药料流动过程仿真, 剪切分布如图 6所示。由图中可知, 三种配方的药料剪切速率分布情况基本一致, 整体分布较为均匀, 表现出很好的层流流动状态, 收缩段和成型段交界处, 药料与模针和壁面相接处位置部分, 剪切速率较大, 在这些部位容易出现非稳态流动表面粗糙、裂纹等现象。以成型段入口为原点, 绘制距离原点分别为0、-0.01、-0.02、-0.03、-0.04、-0.05、-0.06、-0.07、-0.08、-0.09坐标处剪切速率变化如图 7所示。结果表示:药料在成型段过程中, 剪切速率逐渐缓慢增大直至匀速, 这个过程主要是剪切应力的一种缓慢释放过程, 所以模具成型段必须要保证一定的长度才能制出合格尺寸的发射药; 在出口位置(-0.04 m) 出现较大的剪切速率突减现象, 这是由药料中硝化棉分子不再受到外力挤压发生充分回弹, 剪切应力得到释放导致, 该过程容易产生出口压伸变形。
|
图 6 压伸流动过程剪切速率分布 Fig.6 Distribution of shear rate in extruding process |
|
图 7 不同位置剪切速率变化曲线 Fig.7 Curves of change in shear rate at different positions |
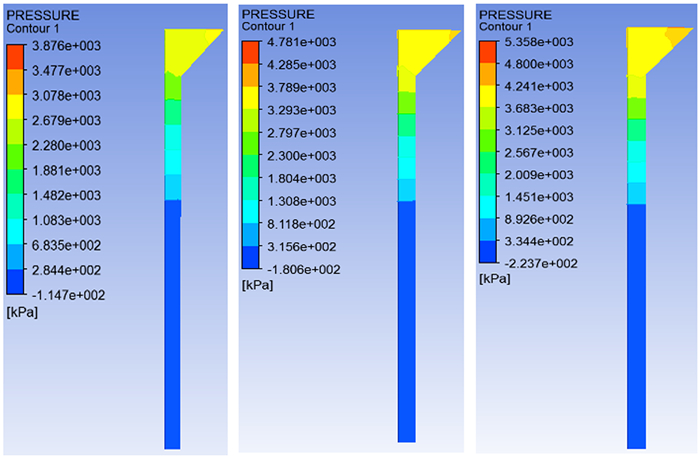
硝基胍发射药压伸压力分布云图如图 8所示。从仿真结果来看, 沿着发射药流动方向, 随着药料高度下降, 压力产生较为明显的压力降, 出口处压力达到稳定。不同位置压力如图 9所示, 随着硝基胍含量的增多, 压力逐渐升高, 这是由硝基胍填料增多造成药料体系粘度升高导致。不同配方条件下, 压力趋势一致, 入口处压力最大, 三种入口处压力分别为4200, 3500, 2500 kPa, 之后沿着药料流动方向减小, 收缩段压力下降缓慢, 成型段压力呈快速均匀下降。这是由于收缩段呈倒锥形状, 药料中的硝化棉分子流动过程中受到来自其周围分子的阻力较大, 压力下降缓慢, 同时在流动过程中可以使发射药密实; 成型段过程中, 截面面积不再变化, 药料流动趋于稳定, 硝化棉分子受到来自其周围的阻力不再发生变化, 压力降呈现匀速变化趋势; 自由段过程中, 药料不再受到其它外力挤压, 压力降为0趋于稳定。
|
图 8 压伸流动过程压力分布 Fig.8 Distribution of pressure in extruding process |

|
图 9 不同位置压力变化曲线 Fig.9 Curves of change in pressure at different positions |
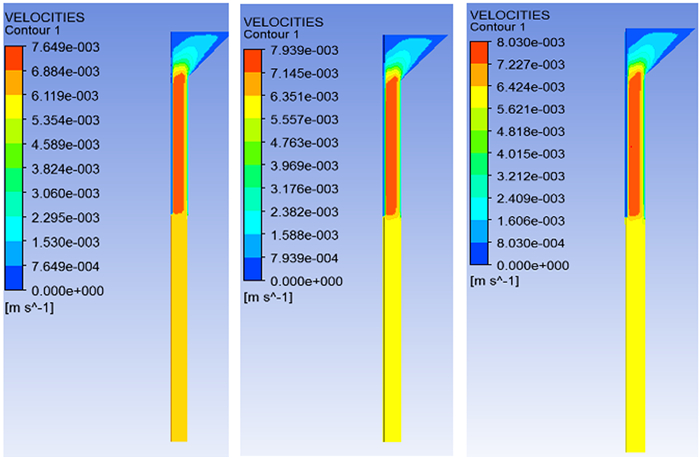
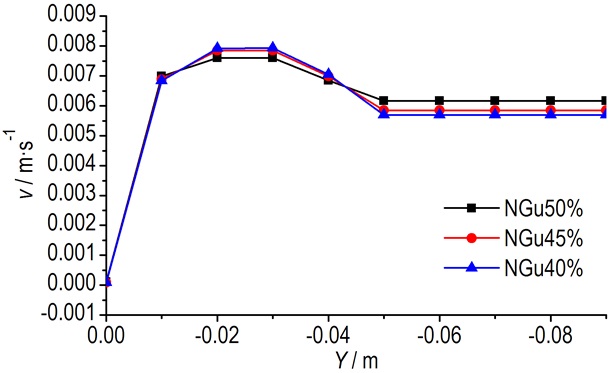
硝基胍药料压伸速度分布云图如图 10所示。从云图结果看, 沿药料流动方向, 收缩段速度逐渐增大直至到成型段, 成型段过程中, 速度基本分别以7.5×10-3, 7.9×10-3, 8.0×10-3 m·s-1保持匀速, 截面速度呈现中间速度大而两侧速度较小。这是由于在近壁面处发射药受到来自模具内表面以及模针表面的阻力较大, 速度接近0。图 11为不同位置速度的仿真结果。结果表明:硝基胍含量变化对药料体系流动速度变化趋势相似; 收缩段过程中, 速度变化基本相同, 都从0逐渐增大到7.0×10-3 m·s-1, 成型段速度基本在7.5×10-3 m·s-1, 自由段分别以6.0×10-3, 5.8×10-3, 5.5×10-3 m·s-1保持匀速。速度波动不大, 能够保证成型硝基胍发射药良好的均匀密实性。
|
图 10 压伸流动过程速度分布 Fig.10 Distribution of velocity in extruding process |
|
图 11 不同位置速度变化曲线 Fig.11 Curves of change in velocities at different positions |
双基吸收药片(TG-1), 针状硝基胍(NGu), 四川255厂; 乙醇, 丙酮, 分析纯, 南京化学试剂有限公司。
捏合机, JH-500, 上海红星化工机械厂; 毛细流变仪, Rosand RH2000, 英国Malvern公司。
4.2 硝基胍发射药制备及流变实验为验证仿真结果, 按表 1所示配方, 加入部分混合溶剂, 利用捏合机将TG-1吸收药片进行初步捏合, 其中醇酮混合溶剂(混合密度0.8 g·cm-3) 总质量与TG-1和硝基胍发射药总质量比为0.24, 捏合机水浴温度控制在35 ℃, 将称量好的TG-1一次性投入到捏合机中, 量取1/2体积的混合溶剂加入捏合机中, 捏合半小时。此时将硝基胍投入捏合机中, 加入剩余混合溶剂, 充分捏合后取出物料, 立即放入密封容器中备用。一部分投入到药缸中进行压伸实验, 测定其成型尺寸。
另外一部分, 分别称取20 g硝基胍发射药药料投入到RH-2000型毛细管流变仪料筒中, 通过水浴加热调整温度35 ℃, 程序设定剪切速率范围, 结合口模和料筒参数, 测定三种配方硝基胍发射药药料的流变性能。
4.3 仿真结果验证模具内流道参数(如针间距) 对硝基胍发射药成型尺寸有一定影响, 定义针间距为2.25 mm和2.30 mm, 保持其它参数不变, 分别对这两种模型进行仿真, 测量设计截面尺寸和仿真成型截面尺寸, 结果如表 6。由表 6可知, 调整针间距主要对内外弧厚和孔径有一定的影响, 对成型的外径基本没有影响。
| 表 6 不同针间距设计截面尺寸和仿真成型尺寸 Tab.6 Design section sizes and simulation extrusion section sizes of different needle spacing |
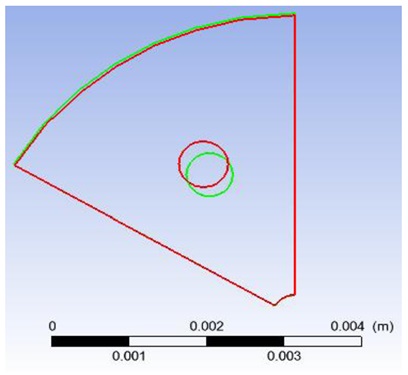
以针间距2.25 mm硝基胍发射药模具为对象, 仿真结果如图 12所示, 绿色曲线代表挤出物截面, 红色曲线代表模具流道截面。从截面对比图可知, 成型发射药形状与模具流道形状一致, 尺寸有一定偏差。这是由于在压伸过程中, 由于壁面和模针的存在, 阻碍药料的充分流动, 药料出模具后不再受到其它方向约束, 药料中的硝化棉大分子链回弹产生变形, 造成实际形状尺寸和模具尺寸产生不同, 与上述剪切速率分布云图以及曲线得出结论一致。
|
图 12 药料仿真挤出截面与内流道截面对比 Fig.12 Comparison of the simulated extrusion section and the inner flow channel section |
根据仿真工艺条件, 选取配方2对硝基胍发射药进行压伸, 并对硝基胍发射药挤出结果进行测量如图 13, 测得外径、孔径以及内外弧厚等参数。与仿真结果对比如表 7, 外径误差为4.36%, 外弧厚误差为7.89%, 内弧厚为3.10%, 孔径误差为9.26%, 中心孔径误差为5.36%, 表明建立数值仿真方法能够较好描述硝基胍发射药压伸流动过程。

|
图 13 硝基胍发射药尺寸测量 Fig.13 Measurement size of NGu gun propellant |
| 表 7 发射药实验结果与仿真尺寸对比 Tab.7 Comparison of the experimental results and simulated ones of gun propellant |
(1) 入口流量为5×10-8 m3·s-1时, 不同配方压力降趋势相似, 收缩段压力下降缓慢, 成型段过程中, 压力降呈现快速均匀下降趋势。
(2) 相同条件下, 不同配方速度变化一致, 收缩段速度从0匀加速至6.5×10-3 m·s-1, 成型段速度因配方不同而略有波动, 但都稳定在7.0×10-3 m·s-1, 出口自由段速度保持匀速不再变化。
(3) 相同条件下, 不同配方发射药剪切速率都呈现较好的稳态流动过程, 在收缩段和成型段交界处以及壁面处容易产生剪切流动造成表面粗糙裂纹以及挤出变形, 因此必须保证成型段具有合适高度。
(4) 采用数值分析方法对不同配方硝基胍发射药压伸过程进行数值仿真, 与实验结果对比, 发射药尺寸参数误差率小于10%。
通过数值仿真的方法能够较准确预测多孔硝基胍发射药压伸过程, 可以显著降低实验成本, 提高模具研制效率, 为实现硝基胍发射药精密制造和压伸工艺优化提供了理论支持。
| [1] |
韩博.高增面性大弧厚硝基胍发射药工艺技术研究[D].南京理工大学, 2009: 33-50.
Han B. Studies onprocess teehnology of high progressive and large web NQ-based gun propellant[D]. Nanjing University of Science and Technology, 2009: 33-50. |
| [2] | Tora E, Dahlquist E. CFD ASnsys-fluent Simulation of prevention of dioxins formation via controlling homogeneous mass and heat transfer within circulated fluidized bed combustor[J]. Energy Procedia, 2015, 75: 130-136. DOI:10.1016/j.egypro.2015.07.236 |
| [3] | Biglione J, Béreaux Y, Charmeau J Y, et al. Numerical simulation and optimization of the injection blow molding of polypropylene bottles-a single stage process[J]. International Journal of Material Forming, 2015 |
| [4] | Laun H M, Schmidt G. Rheotens tests and viscoelastic simulations related to high-speed spinning of polyamide[J]. Journal of Non-Newtonian Fluid Mechanics, 2015, 222: 45-55. DOI:10.1016/j.jnnfm.2014.08.018 |
| [5] | Ahmed R, Liang R F, Mackley M R. The experimental observation and numerical prediction of planar entry flow and die swell for molten polyethylenes[J]. Journal of Non-Newtonian Fluid Mechanics, 1995, 59(2-3): 129-153. DOI:10.1016/0377-0257(95)01358-3 |
| [6] | Yang K, Xin C, Yu D, et al. Numerical simulation and experimental study of pressure and residence time distribution of triple-screw extruder[J]. Polymer Engineering & Science, 2015, 55(1): 156-162. |
| [7] | Zhou Ke H Z Y S. Numerical simulation for exploring the effect of viscosity on single-screw extrusion process of propellant: ISSST[Z]. 2014. |
| [8] |
钟婷婷.双基推进剂螺压挤出成型工艺流变特性的数值模拟研究[D].南京:南京理工大学, 2015.
ZHONG Ting-ting. Numerical simulation research of rheological behavior for the screw extrusion molding process of double-base propellant[D]. Nanjing: Nanjing University of Science and Technology, 2015. |
| [9] |
霍朝沛.双螺杆混合含铝炸药模拟物数值模拟及均匀性研究[D].北京:北京化工大学, 2015.
HUO Chao-pei. Numerical simulation and mixing uniformity analysis of aluminized explosives simulants mixed in twin screw extruder[D]. Beijing: Beijing University of Chemical Technology, 2015. |
| [10] |
刘林林, 马忠亮, 高可政, 等. 变燃速发射药挤出过程中药料流动计算研究[J].
含能材料, 2010, 18(5): 583-586. LUI Lin-lin, MA Zhong-liang, GAO Ke-zhen. Computationalstudy of flow for outside layer of variable-burning rate propellant during extrusion[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2010, 18(5): 583-586. |
| [11] |
张丹丹, 何卫东. 硝基胍七孔发射药挤压成型过程的数值模拟[J].
火炸药学报, 2015, 38(1): 82-86. ZHANG Dan-dan, HE Wei-dong. Numerical simulation of 7-hole nitroguanidine-based gun propellant in extrusion forming process[J]. Chinese Journal of Explosives & Propellants, 2015, 38(1): 82-86. |
The shear rate field, pressure field and velocity field of porous nitroguanidine gun propellant in different extrusion processes were analyzed by the FEM method. The sizes of 7-pore NGu gun propellant were measured and compared with simulation sizes.




