2. 陕西师范大学, 陕西 西安 710062
2. Shaanxi Normal University, Xi′an 710062, China
全氮材料具有能量高、无污染的优点, 是潜在的新型高能量密度材料[1-5]。然而, 全氮材料的合成尚处于实验室探索阶段, 难以获得其实际样品, 如何获取全氮材料在世界范围内仍然是一个巨大的挑战。因此, 对于全氮材料的能量性质, 特别是爆轰性能, 只能通过理论方法进行预测。
晶体密度是决定全氮材料爆轰性能的重要参数, 其预测方法主要有两类:一是基于分子体积的半经验方法[6-10]; 一是基于晶体体积的分子力学方法[11-12]。前者缺乏实验数据难以获得准确的经验参数, 且忽略了分子间相互作用对晶体堆积结构的影响, 在原理上不够精确。后者缺乏完全适用于全氮结构的力场参数, 无法准确描述全氮分子间的相互作用, 致使晶体结构预测存在较大偏差。
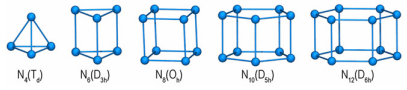
目前, 国际上关于全氮材料晶体密度预测研究中, 最有代表性和被广泛引用的报道来自于——英国QinetiQ公司[13]和瑞典国防研究院FOI[14]。二者均采用分子力学方法预测了5种笼形全氮结构的晶体密度(见图 1), 但预测结果却存在较大差异。例如, 对于N4(Td) 结构, QinetiQ预测的晶体密度为1.752 g·cm-3, 而FOI的预测结果为2.3 g·cm-3。
|
图 1 典型笼形全氮分子结构示意图 Fig.1 Schematic diagram of typical all-nitrogen molecular structures with cage type |
为了准确预测全氮材料的晶体密度, 本研究基于量子化学计算方法, 建立了适用于全氮结构的力场参数。与传统分子力场相比, 该力场具有“特异性”, 即每个全氮结构均具有一套独立的参数, 尤其是范德华参数; 而在传统分子力场中, 通常是一类分子采用一套相同的参数。例如, 对于笼形全氮结构均采用相同的范德华参数, 这将难以区分全氮结构差异对晶体密度的影响, 势必带来较大误差。
通过建立特异性力场参数, 本研究共预测了20种全氮材料的晶体结构, 基于晶体体积计算了晶体密度。为了与国外文献相比较, 仅列出了5种笼形全氮结构的晶体密度预测结果, 重点介绍方法的建立。
2 计算方法 2.1 分子内力场参数采用密度泛函理论B3LYP/6-31G (d) 方法[15-16], 通过Gaussian程序[17]优化全氮分子的几何构型, 在最优构型的基础上进行振动频率分析, 借助VMD程序[18]中Paratool插件将Hessian矩阵中的特征振动模式分解投影到内坐标上, 得到键长、键角、二面角的平衡值及相应的力常数等分子内力场参数。分子内势能函数形式如下:
| $ {E_{{\rm{intra}}}} = \sum {E_{{\rm{bond}}}} + \sum {E_{{\rm{angle}}}} + \sum {E_{{\rm{dihedral}}}} $ | (1) |
| $ {E_{{\rm{bond}}}} = \frac{{{K_b}}}{2}\left( {b - {b_0}} \right) $ | (2) |
| $ {E_{{\rm{angle}}}} = \frac{{{K_\theta }}}{2}\left( {\theta - {\theta _0}} \right) $ | (3) |
| $ {E_{{\rm{dihedral}}}} = \frac{{{K_\varphi }}}{2}\{ 1 - {\rm{cos}}[n(\varphi - {\varphi _0})]\} $ | (4) |
式中, Ebond, Eangle和Edihedral分别为化学键、键角与二面角势能项; b0, θ0, φ0分别为键长、键角及二面角的平衡值; Kb, Kθ, Kφ为相应的力常数; n为多重度参数。建立分子内力场参数的目的是为了保证全氮结构的合理性, 尤其是在分子间范德华参数优化过程中, 需要避免全氮结构发生较大偏差。
2.2 分子间力场参数分子间势能分为静电与范德华相互作用能, 分别由库仑定律和Lennard-Jones函数描述, 具体函数形式如下:
| $ {E_{{\rm{inter}}}} = \sum {E_{{\rm{elec}}}} + \sum {E_{{\rm{vdW}}}} $ | (5) |
| $ {E_{{\rm{elec}}}} = \frac{{{q_i}{q_j}}}{{4\pi {D_0}{r_{ij}}}} $ | (6) |
| $ {E_{{\rm{vdW}}}} = \varepsilon \left[ {{{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^{12}} - 2{{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^6}} \right] $ | (7) |
式中, Eelec和EvdW分别为静电和范德华相互作用势能项; i和j为不同分子上的氮原子; qi和qj为原子点电荷; D0为介电常数; rij为两个原子之间的距离; ε为势阱深度; σ是作用势为0时原子间的距离。
全氮分子只有一种原子类型N, 其电负性是一致的, 对于对称性高的结构(如文中所列笼形结构), 原子点电荷为0。对于对称性较差的全氮结构, 由于氮原子周围化学环境不尽相同, 因此具有微弱的静电相互作用。总之, 全氮分子间作用主要由范德华参数主导, 建立准确的范德华参数对于全氮晶体密度的预测至关重要。
首先, 采用B3LYP/6-31G (d) 方法拟合全氮分子静电势得到ESP电荷, 将其指定为原子点电荷, 由库仑定律计算分子间静电相互作用能。对于范德华参数, 采用文献[19]的方法进行优化, 主要原理为:在尽可能穷尽全氮分子二聚体结构的条件下, 优化范德华参数使分子力学方法计算的二聚体结合能与量子化学计算的二聚体结合能均方根误差(RMSE) 最小。RMSE定义如下:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{(E_k^{{\rm{QM}}} - E_k^{{\rm{MM}}})}^2}} } $ | (8) |
式中, N为二聚体结构抽样总数, k为其中一次抽样, EkQM与EkMM分别表示量子化学与分子力学计算的二聚体结合能。
为了避免二聚体抽样的人为性与任意性, 采用Monte-Carlo方法随机产生一定密度下含有大量全氮分子的无定形结构, 以任意两个全氮分子之间的质心距离为判据进行二聚体的抽样。无定形结构由Material Studio软件[20]中Amorphous Cell模块构建, 密度设置为0.6~0.8 g·cm-3, 范德华参数采用Dreiding力场[21]默认参数, 其余力场参数为经优化后的新参数。
对每个抽取的二聚体结构, 均采用MP2/cc-pvtz[22-23]方法计算结合能Ebind:
| $ {E_{{\rm{bind}}}} = {E_{{\rm{AB}}}} - {E_{\rm{A}}} - {E_{\rm{B}}} $ | (9) |
式中, EAB, EA和EB分别为二聚体AB、二聚体中单体A与B的能量, J。在分别得到量子化学和分子力学计算的二聚体结合能之后, 使用Quasi-Newton算法对范德华参数进行优化。
2.3 晶体堆积结构基于建立的全氮分子特异性力场参数, 使用Materials Studio程序[20]中Polymorph模块, 将全氮分子按照晶体空间点群进行堆积, 预测全氮分子的晶体结构, 取晶格能最低的晶型, 根据晶胞参数计算晶体密度。
3 结果与讨论全氮分子的晶体密度主要取决于分子间相互作用, 因此范德华参数的准确程度对于晶体密度预测至关重要。由范德华参数的优化过程可知, 影响范德华参数的因素很多, 诸如二聚体抽样个数, 二聚体结合能是否校正, 范德华参数种类等, 为了得到相对稳定的范德华参数, 分别对以上影响因素作了考察。另外, 由于Dreiding力场中范德华参数也采用了Lennard-Jones (12-6) 函数形式, 且在二聚体构建中作为初始值赋予全氮结构, 因此, 本研究优化的范德华参数与Dreiding力场参数也进行了比较。需要注意的是: Dreiding力场中N原子的范德华参数具有唯一数值, 即ε=0.3238 kJ·mol-1、σ=3.6621 Å, 为了表达简洁, 在余下的表格中不再提及, 而仅列出本文优化所得的范德华参数。
3.1 抽样个数以200个N4(Td) 分子构建的无定形结构为例, 密度分别设置为0.8和0.6 g·cm-3, 抽取任意两个质心距离小于15 Å的二聚体结构, 抽样个数分别为4382和3231。表 1为不同抽样个数下优化的N4(Td) 范德华参数。从表 1中可以看出, 两种抽样个数下优化的范德华参数相差不大, RMSE提高不到1%, 说明基于无定形结构的抽样策略能够得到比较稳定的范德华参数。另外, 与Dreiding力场参数相比, 优化后ε变大、表 1抽样个数对范德华参数的影响σ变小, 说明N4(Td) 二聚体相互作用更强、结合更加紧密, 且RMSE下降了约一个数量级, 说明该参数能够准确地描述N4(Td) 二聚体的分子间相互作用。
| 表 1 抽样个数对范德华参数的影响 Tab.1 Effect of sampling number on the van der Waals (vdW) parameters |
通过量子化学计算全氮二聚体结合能时, 由于存在基组重叠效应, 采用式(9) 得到的二聚体结合能一般要大于真实值, 需要进行校正。以N10(D2h) 为例, 采用counterpoise方法[24]对结合能进行了校正, 并考察了其对范德华参数的影响。如表 2所示, 结合能经过校正后, 优化的范德华参数与Dreiding力场参数的RMSE相差不大, 说明Dreiding力场能够较好地描述环型全氮分子, 但对笼形全氮分子的预测精度较差(见表 1)。如果结合能不经过校正, Dreiding力场参数的RMSE则从0.358增加到0.686。对比校正前后的范德华参数可以发现, 未校正的ε较大、σ较小, 即分子间相互作用更强, 从而高估了二聚体结合能。因此, 对结合能进行校正是必要的。
| 表 2 结合能校正及参数个数对范德华参数的影响 Tab.2 Effect of binding energy correction and parameter numbers on the van der Waals parameters |
基于全氮结构对称性, 可以根据化学环境定义不同的氮原子类型。例如, 对于N4(Td) 分子, 每个氮原子周围化学环境相同, 只需定义一种原子类型; 对于N10(D2h) 分子, 则可以进一步分为两种原子类型, 即环上原子与桥原子。因此, 以N10(D2h) 为例, 考察了原子类型种类对范德华参数的影响。如表 2所示, 无论结合能校正与否, 双原子类型与单原子类型相比, RMSE相差不大, 准确程度提高有限, 说明采用单原子类型已经能够很好地描述全氮分子间相互作用。
综上, 采用无定形结构抽样方法可以得到相对稳定的范德华参数, 二聚体结合能的量子化学计算需要进行校正, 没有必要将同一全氮分子内的氮原子类型进行精细的分类。因此, 全氮分子的范德华参数优化均采用如下设置:无定形结构构建时盒子密度设置为0.6 g·cm-3, 对二聚体结合能进行校正, 每个全氮分子只定义一种原子类型。
3.4 参数特异性表 3列出了笼形全氮分子经优化后的范德华参数, 与Dreiding力场相比, 优化的范德华参数RMSE降低了约一个数量级, 准确程度大幅提高。ε集中在0.4~0.7 kJ·mol-1, σ集中在3.2~3.4 Å, 说明对于不同的笼形结构, 全氮分子的范德华参数确实存在特异性, 只采用一种普适的氮原子参数不能准确地描述所有的笼形全氮结构。另外, 随着氮原子数的增加, ε与σ并没有呈现明显的规律。其中, N4(Td) 的ε最大, σ也最大; N8(Oh) 的ε最小, σ仅大于N12(D6h); N12(D6h) 的σ最小, ε仅小于N4(Td)。究其原因, 是笼形全氮分子特殊的空间结构所致。
| 表 3 笼形全氮分子范德华参数 Tab.3 The van der Waals parameters of all-nitrogen molecules with cage structure |
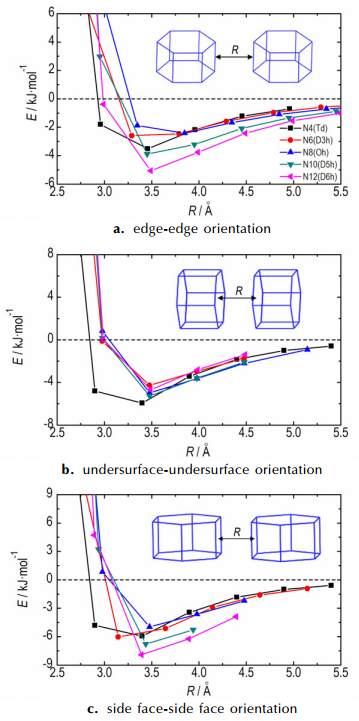
为了解释笼形全氮分子范德华参数的特异性, 采用MP2/cc-pvtz方法分别计算了笼形全氮分子棱-棱、底面-底面和侧面-侧面三种空间取向下的二聚体结合能与相对距离的关系图, 结果示于图 2。由图中可知, 不同空间取向下笼形全氮分子的平衡距离是较为接近的, 差异主要体现在势阱深度上。对于棱-棱取向, N12(D6h) 势阱深度最大, 其次为N10(D5h) 与N4(Td); 对于底面-底面取向, 尽管N4(Td) 底面上只有3个氮原子, 却显示出了最强的分子间相互作用; 对于侧面-侧面取向, 除了N4(Td) 外, 其余笼形结构侧面上均有4个氮原子, N12(D6h) 结合能最大, N10(D5h) 与N4(Td) 次之。综合所有取向可知, N4(Td) 与N12(D6h) 作用势最大, 这与其空间结构特点是密切相关的, 同时也可看出优化的范德华参数是合理的。
|
图 2 不同空间取向的笼形全氮二聚体结合能与相对距离关系图 Fig.2 The binding energies of all-nitrogen dimer with cage structure as a function of distance for different orientations |
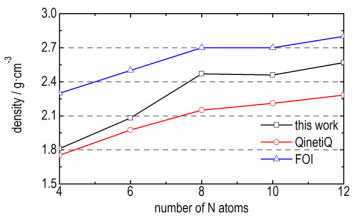
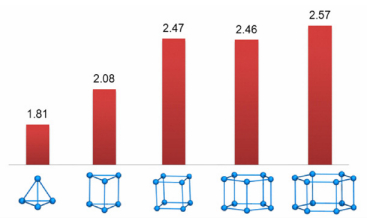
基于建立的分子力场参数, 预测了20种全氮分子的晶体密度, 为了便于和英国QinetiQ公司、瑞典国防研究院FOI的计算结果相比较, 只列出了N4(Td)、N6(D3h)、N8(Oh)、N10(D5h) 及N12(D6h) 共计5种笼形全氮分子的晶体密度, 结果依次为1.81, 2.08, 2.47, 2.46, 2.57 g·cm-3。除N4(Td) 外, 其余全氮分子的晶体密度均在2.0 g·cm-3以上, 其中N12(D6h) 晶体密度最高。由图 3可见, 本研究结果介于文献计算结果的范围之内。随着氮原子数的增加, 本研究预测的晶体密度并没有呈简单的增长趋势, 而是在N8(Oh) 出现了一个突变点, 这表明特异性力场参数的计算结果更加合理。
|
图 3 晶体密度预测值与笼形全氮原子数关系图 Fig.3 Predicted crystal densities of all-nitrogen molecules with cage type as a function of nitrogen atom number |
(1) 采用量子化学计算方法, 建立了适用于全氮结构的“特异性”力场参数, 即针对特定的全氮分子, 建立了一套独立的力场参数。由5种笼形全氮结构棱-棱、底面-底面、侧面-侧面取向的二聚体结合能可知, 不同结构的全氮分子间相互作用确实存在差异, 如只采用一套通用的力场参数势必带来较大误差。因此, 特异性力场参数在原理上更加精确合理。
(2) 范德华力是全氮分子在晶体堆积中的主导作用力, 本研究详细讨论了范德华参数的优化策略, 包括二聚体抽样个数, 二聚体结合能是否校正, 参数种类等影响因素, 与Dreiding力场中范德华参数相比, 通过特异性参数计算的二聚体结合能与量子化学计算结果的均方根误差降低了约一个数量级。
(3) 借助特异性力场参数, 预测了20种全氮分子的晶体密度。其中, N4(Td)、N6(D3h)、N8(Oh)、N10(D5h) 及N12(D6h) 五种笼形全氮分子的晶体密度分别为1.81,2.08,2.47,2.46, 2.57 g·cm-3, 介于英国QinetiQ公与瑞典国防研究院FOI报道结果的范围之间, 体现了特异性力场参数的真实性。基于本研究预测的晶体密度, 有助于进一步探索笼形全氮分子的爆轰性能。
| [1] | Eremets M I, Gavriliuk A G, Trojan I A, et al. Single-bonded cubic form of nitrogen[J]. Nature Materials, 2004, 3(8): 558-563. DOI:10.1038/nmat1146 |
| [2] | Samartzis P C, Wodtke A M. All-nitrogen chemistry: how far are we from N60?[J]. International Reviews in Physical Chemistry, 2006, 25(4): 527-552. DOI:10.1080/01442350600879319 |
| [3] | Hirshberg B, Gerber R B, Krylov A I. Calculations predict a stable molecular crystal of N8[J]. Nature Chemistry, 2014, 6(1): 52-56. |
| [4] |
李玉川, 庞思平. 全氮型超高能含能材料研究进展[J].
火炸药学报, 2012, 35(1): 1-8. LI Yu-chuan, PANG Si-ping. Progress of all-nitrogen ultrahigh-energetic material[J]. Chinese Journal of Explosive & Propellants, 2012, 35(1): 1-8. |
| [5] |
张光全, 董海山. 氮簇合物——潜在的高能量密度材料候选物[J].
含能材料, 2004, 12(Suppl.): 105-113. ZHANG Guang-quan, DONG Hai-shan. Nitrogen clusters-potential candidates as high-energy density materials[J]. Chinese Journal of Energetic Materials (Hanneng Cailiao), 2004, 12(Suppl.): 105-113. |
| [6] | Tarver C M. Density estimations for explosives and related compounds using the group additivity approach[J]. Journal of Chemical and Engineering Data, 1979, 24(2): 136-145. DOI:10.1021/je60081a006 |
| [7] | Ammon H L, Mitchell S. A new atom/functional group volume additivity data base for the calculation of the crystal densities of C, H, N, O and F-containing compounds[J]. Propellants, Explosives, Pyrotechnics, 1998, 23(5): 260-265. DOI:10.1002/(ISSN)1521-4087 |
| [8] | Piacenza G, Legsaï G, Blaive B, et al. Molecular volumes and densities of liquids and solids by molecular mechanics-estimation and analysis[J]. Journal of Physical Organic Chemistry, 1996, 9(6): 427-432. DOI:10.1002/(ISSN)1099-1395 |
| [9] | Wong M W, Wiberg K B, Frisch M J. Ab initio calculation of molar volumes: comparison with experiment and use in solvation models[J]. Journal of Computational Chemistry, 1995, 16(3): 385-394. DOI:10.1002/(ISSN)1096-987X |
| [10] | Politzer P, Martinez J, Murray J S, et al. An electrostatic interaction correction for improved crystal density prediction[J]. Molecular Physics, 2009, 107(19): 2095-2101. DOI:10.1080/00268970903156306 |
| [11] | Holden J R, Du Z Y, Ammon H L. Prediction of possible crystal structures for C-, H-, N-, O-, and F-containing organic compounds[J]. Journal of Computational Chemistry, 1993, 14(4): 422-437. DOI:10.1002/(ISSN)1096-987X |
| [12] | Dzyabchenko A V, Pivina T S, Arnautova E A. Prediction of structure and density for organic nitramines[J]. Journal of Molecular Structure, 1996, 378(2): 67-82. |
| [13] | Haskins P J, Fellows J, Cook M D, et al. Molecular level studies of polynitrogen explosives[C]//12th International Detonation Symposium, California, 2002. |
| [14] | Östmark H. High energy density materials (HEDM): overview, theory and synthetic efforts at FOI[C]//New Trends in Research of Energetic Materials, Czech Republic, 2006: 231-250. |
| [15] | Lee C, Yang W, Parr R G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density[J]. Physical Review B, 1988, 37(2): 785-789. DOI:10.1103/PhysRevB.37.785 |
| [16] | Becke A D. Density-functional thermochemistry. Ⅲ. The role of exact exchange[J]. Journal of Chemical Physics, 1993, 98(7): 5648-5652. DOI:10.1063/1.464913 |
| [17] | Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 09[C]//Gaussian, Inc., Wallingford CT, 2009. |
| [18] | Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics[J]. Journal of Molecular Graphics, 1996, 14(1): 33-38. DOI:10.1016/0263-7855(96)00018-5 |
| [19] | Kramer C, Gedeck P, Meuwly M. Multipole-based force fields from ab initio interaction energies and the need for jointly refitting all intermolecular parameters[J]. Journal of Chemical Theory and Computation, 2013, 9(3): 1499-1511. DOI:10.1021/ct300888f |
| [20] | Material Studio 8.0[C]//Acceryls Inc.: San Diego, 2014. |
| [21] | Mayo S L, Olafson B D, Goddard W A. Dreiding: A generic force field for molecular simulations[J]. Journal of Physical Chemistry, 1990, 94(26): 8897-8909. DOI:10.1021/j100389a010 |
| [22] | Head-Gordon M, Pople J A, Frisch M J. MP2 energy evaluation by direct methods[J]. Chemical Physics Letters, 1988, 153(6): 503-506. DOI:10.1016/0009-2614(88)85250-3 |
| [23] | Kendall R A, Dunning Jr. T H, Harrison R J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions[J]. Journal of Chemical Physics, 1992, 96(9): 6796-6806. DOI:10.1063/1.462569 |
| [24] | Boys S F, Bernardi F. Calculation of small molecular interactions by differences of separate total energies-some procedures with reduced errors[J]. Molecular Physics, 1970, 19(4): 553-566. DOI:10.1080/00268977000101561 |
The force field parameters for specific all-nitrogen molecules were calculated on the basis of quantum chemical method, and the crystal densities of five representative all-nitrogen molecules with cage structure were predicted by molecular mechanics methods.