2. 北京航天长征飞行器研究所, 北京 100076
2. Beijing Institute of Space Long Munch Vehicle, Beijing 100076, China
端羟基聚丁二烯(HTPB)作为广泛应用于推进剂配方[1-3]和聚合物粘结炸药(PBX)[4-6]中的粘结剂材料, 其力学行为直接影响推进剂和PBX的动力学行为和安全性。为深入研究推进剂及PBX的动力学特性, 为多尺度模拟计算及力、热、化学反应耦合的数值模拟分析提供精确的组分参数, 有必要对HTPB的力学行为进行深入研究。
Gupta[7]用气炮研究了0.8 GPa下HTPB粘结剂的动力学特性, 认为在该压力范围内, 该粘结剂在冲击加载下的率无关特性, Millett[8]则利用气炮研究了HTPB在2.5GPa下的冲击Hugoniot关系, 认为在该冲击压力内, 该粘结剂材料具有线性的冲击Hugoniot关系和率无关性, 回收实验表明, 经历了该冲击加载后, HTPB回收样品的玻璃化转变温度、分解温度及分子量均未发生改变, 显示出优越的力学和化学稳定性。Hall[9]利用Z装置对HTPB粘结剂进行了无冲击斜波加载, 获得了HTPB的速度响应历史, 模拟计算中采用Millett[8]的线性Hugoniot模型参数不能重现实验结果, 认为在斜波加载下, HTPB表现出非线性行为, 线性Hugoniot模型不能如实反映实验结果, 该结论与冲击实验的结果存在差异。目前国内外针对HTPB推进剂及炸药的力学行为研究相对较多, 对HTPB粘结剂在动载下的动力学行为研究相对缺乏, 特别是在高应变率动载下, 实验结果相对较少。
本研究利用磁驱动装置CQ-4, 开展了HTPB粘结剂在斜波加载下的动力学响应实验研究, 利用Lagrange数据处理方法对实验结果进行了解读, 进一步澄清了HTPB在动高压加载下的力学响应特性, 为深入研究基于HTPB的推进剂及炸药的动力学行为奠定基础。
2 HTPB的斜波加载实验 2.1 磁驱动斜波加载实验HTPB预聚体是无色或淡黄色液体, 一般加入甲苯二异氰酸酯(TDI)或异佛尔酮二异氰酸酯(IPDI)作为固化交联剂进行固化。本实验中, 选用TDI对HTPB进行固化, 获得密度约0.95 g·cm-3的半透明样品材料。
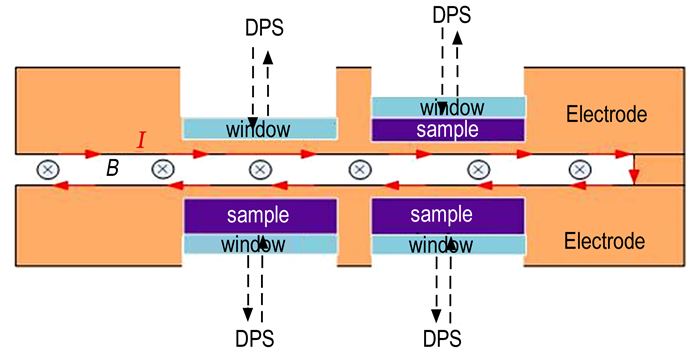
利用磁驱动斜波压缩加载实验技术对实验样品进行加载, 加载装置为中国工程物理研究院流体物理研究所的小型磁驱动装置CQ-4[10]。利用大电流产生的洛伦兹力通过1 mm厚纯铝驱动电极对不同厚度实验样品进行无冲击斜波加载, 利用激光干涉测速技获得不同厚度实验样品的速度响应数据, 进而处理获得样品在该加载条件下的力学特性[11-12]。负载区样品安装示意图见图 1所示。
|
图 1 负载区结构示意图 Fig.1 Sketch map of Loading area |
采用光学性能稳定的LiF(100) 单晶作为测试窗口, 窗口厚度5 mm, LiF窗口一面镀300 nm铝膜, 一面镀1550 nm波长增透膜, 实验样品与纯铝驱动电极、窗口之间采用粘性系数极低的双组份环氧胶胶结, 保证负载区样品与驱动电极及窗口间无间隙且加载过程为一维无冲击加载。本次加载实验号为CQ-4-Shot-293, 同时加载三种不同厚度(0.65, 1.095, 1.21 mm, )HTPB实验样品, 另一样品安装位置直接安装LiF窗口, 对应实验曲线中的0 mm样品, 通过测量纯铝电极的速度响应, 计算本次实验的加载压力历史曲线。
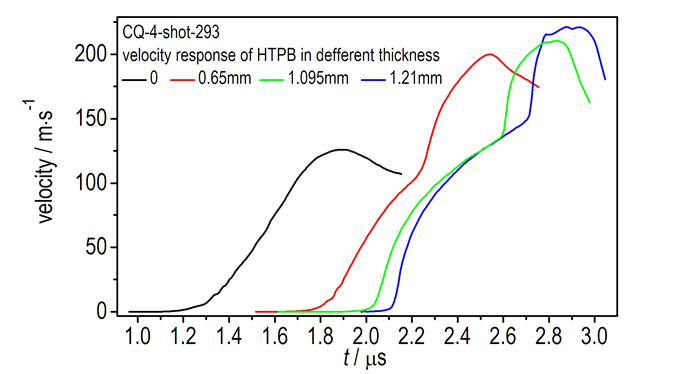
实验中CQ-4装置充电电压40 kV, 利用激光干涉测速获得不同厚度HTPB样品的速度响应曲线。由于LiF窗口折射率的影响, 激光速度干涉仪测得的界面粒子速度ua与界面粒子速度的真实值up存在一定差异, 在0~124 GPa压力范围内, 有公式1所述线性关系[13], 经过修正后获得的真实速度结果见图 2所示。其中黑色曲线为纯铝电极与LiF界面处速度历史响应曲线。实验获得的速度历史曲线匀滑, 在速度上升过程中出现拐折, 且随着样品厚度的增加, 速度曲线陡度增加, 速度拐折随之上升, 厚样品中拐折处形成冲击。该拐折是由于样品和窗口界面处的反射波与加载压力波相互叠加, 改变了后续加载压力历史, 因此数据处理过程中仅考虑速度拐折出现前的速度曲线, 拐折后的速度曲线可以与模拟计算结果比对, 作为对实验数据处理结果的校核。
| ${u_{\rm{p}}} = {u_{\rm{a}}}/1.2678$ | (1) |
式中, ua为未进行折射率修正的速度值, up为修正后的真实速度, 单位均为m·s-1。
|
图 2 CQ-4-Shot-293实验样品速度响应曲线 Fig.2 Experimental velocity curves of CQ-4-Shot-293 |
对图 2实验结果, 不考虑铝电极的速度曲线(0 mm), 仅考虑速度拐折出现前的三种不同厚度样品的速度曲线, 见图 3中黑色曲线所示, 由于炸药与窗口材料波阻抗不匹配, 需先采用增量阻抗匹配方法[14], 修正测量速度为炸药样品的原位粒子速度, 见公式(2) 所示:
| $\Delta {u_{\rm{p}}} = \frac{{{Z_{\rm{s}}} + {Z_{\rm{w}}}}}{{2{Z_{\rm{s}}}}}\Delta {u_{\rm{w}}}$ | (2) |
式中, Δup为炸药粒子速度up的修正量, m·s-1; Δuw为窗口速度(测量速度)的变化, m·s-1; Zs=(ρ0c(uw))s表示样品在界面速度为uw时的波阻抗, kg·s·m-2, Zw=(ρ0c(uw))w表示窗口在界面速度为uw时的波阻抗, kg·s·m-2。
数据处理采用Lagrange方法[15], Lagrange坐标下, 实验材料的p-V线可由公式(3-5) 获得:
| ${c_{\rm{L}}}\left( {{u_{\rm{p}}}} \right) = \frac{{{x_1} - {x_2}}}{{{t_1}\left( {{u_{\rm{p}}}} \right) - {t_2}\left( {{u_{\rm{p}}}} \right)}}$ | (3) |
| ${\rm{d}}p = {\rho _0}{c_{\rm{L}}}\left( {{u_{\rm{p}}}} \right){\rm{d}}{u_{\rm{p}}}$ | (4) |
| ${\left( {\frac{{\partial p}}{{\partial \rho }}} \right)_{\rm{s}}} = \frac{{\rho _0^2}}{{{\rho ^2}}}{\left( {{c_{\rm{L}}}\left( p \right)} \right)^2}$ | (5) |
式中, cL为Lagrange声速, m·s-1; x1, x2分别为两不同厚度样品1和2的厚度, m; up为样品原位粒子速度, m·s-1; t(up)为对应厚度样品原位粒子速度为up时所需的时间, s; p为加载压力, Pa; ρ0和ρ分别为样品初始密度和压缩过程中密度, g·cm-3。
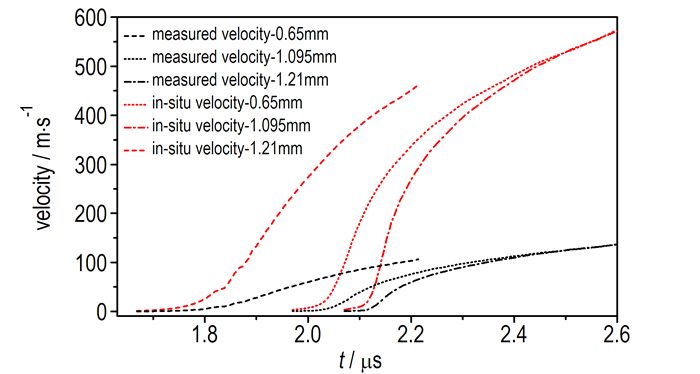
由公式(2)~(5) 迭代计算可得到修正的不同厚度样品的原位粒子速度曲线, 见图 3红色曲线, 图 3给出了对样品响应测量获得的速度(图 2)与样品的原位粒子速度对比。三种不同厚度样品两两作差得到的三条声速-原位粒子速度曲线, 见图 4所示, 图 4中红色实线为对声速的拟合曲线。
在低压下, 假设等熵压缩线与冲击压缩线重合, 即:
| ${p_{\rm{s}}} = \int_0^{{u_{\rm{p}}}} {{\rho _0}{c_{\rm{L}}}{\rm{d}}{u_{\rm{p}}} = {p_{\rm{H}}} = {\rho _0}\left( {{c_0} + \lambda {u_{\rm{p}}}} \right){u_{\rm{p}}}} $ | (6) |
则Lagrange声速-粒子速度关系表现为线性行为[16]:
| ${c_{\rm{L}}} = {c_0} + 2\lambda {u_{\rm{p}}}$ | (7) |
式中, cL为Lagrange声速, m·s-1; c0和λ为Hugoniot关系参数, m·s-1。
|
图 3 出现拐折前的速度曲线和原位粒子速度曲线 Fig.3 Measured velocity and in-situ velocity before the inflection |

|
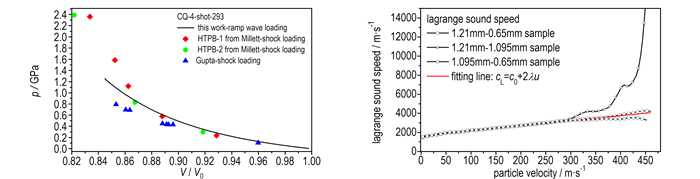
图 4 HTPB样品的拉格朗日声速-粒子速度曲线 Fig.4 The Lagrange sound speed vs. particle velocity of the HTPB samples |
由图 4可见, HTPB样品的cL-up关系表现出线性特征, 与Millett和Gupta利用气炮加载[7-8]获得的结论一致, 与Hall利用Z装置开展的HTPB斜波加载实验[9]的结论相悖。利用公式(7) 对图 4曲线作线性拟合, 得到HTPB实验样品参数见表 1。
| 表 1 HTPB的Hugoniot参数及Millett的气炮实验结果 Tab.1 The Hugoniot parameters of HTPB in this work and gas gun data from Millett |
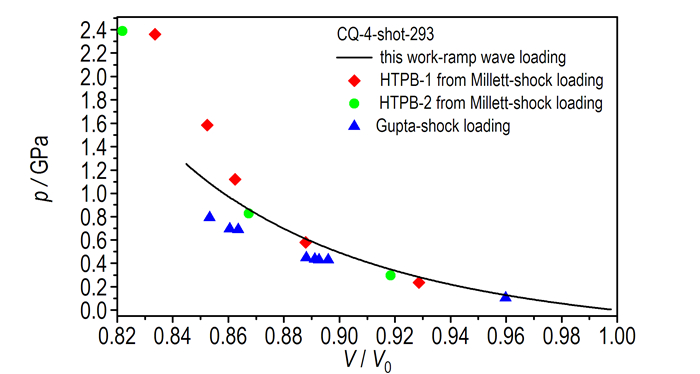
积分公式(4), 获得如图 5所示HTPB的应力-速度曲线关系, 拟合Hugoniot公式(8), 获得图 6 HTPB样品的应力-比容变化曲线。图 5和图 6结果显示, 应力-速度曲线与文献结果重合较好, 应力-比容曲线与文献结果有一定差异, 特别是在压缩后段, 本实验中的HTPB样品显得更易于压缩, 该差异可能与样品制备工艺及密度(表 1)差异有关, 更高压力范围内的比较, 尚需在后续实验中开展更高压力的HTPB斜波压缩实验。

|
图 5 实验获得的HTPB压力-速度曲线及与文献[8]结果的比较 Fig.5 The pressure vs. velocity curve compared with shock loading data from reference[8] |
|
图 6 HTPB压力-比容曲线及与文献[7-8]实验结果的比较 Fig.6 The pressure vs. specific volume curve compared with results from reference[7-8] |
| ${p_{\rm{H}}}\left( V \right) = {p_0}\left( V \right) + \frac{{{\rho _0}c_0^2\eta }}{{{{\left( {1 - \lambda \eta } \right)}^2}}}$ | (8) |
式中, pH是冲击压力, Pa, p0是初始压力, Pa; 压缩度η=1-V/V0, V、V0分别为样品单位体积和样品初始体积, m3。
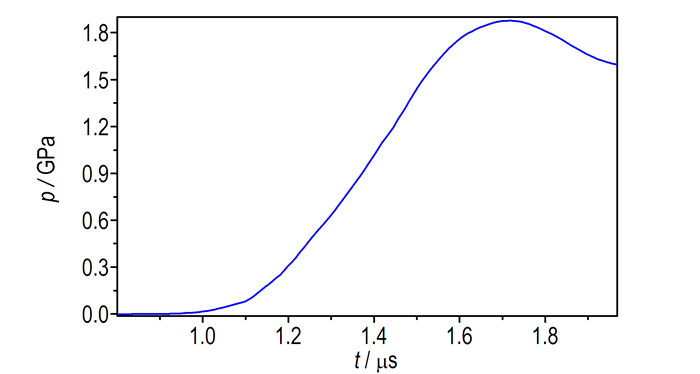
3 一维流体动力学模拟计算由于纯铝和LiF窗口的材料参数已知, 假设加载过程中纯铝电极烧蚀厚度可忽略, 利用反积分数据处理方法[17]对纯铝电极/LiF窗口界面处的速度历史进行处理, 可获得准确的CQ-4-Shot-293实验加载压力历史(图 7), 利用该压力历史和上述实验获得的HTPB的动力学参数, 即可对本实验进行一维流体动力学数值模拟, 以实现对上述实验参数的校核。
|
图 7 CQ-4-Shot-293实验加载压力历史 Fig.7 Loading history of CQ-4-Shot-293 |
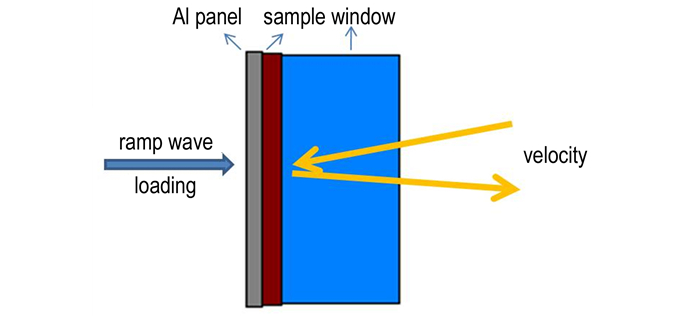
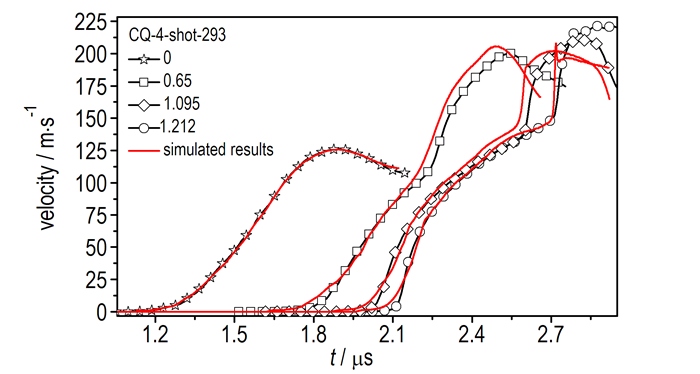
CQ-4-Shot-293实验数值模拟模型如图 8所示, 纯铝电极和LiF和HTPB样品采用Gruneison状态方程, 即上述式(8), HTPB在实验中未见弹塑性转变, 未考虑材料的强度效应, 计算参数列表于表 2。利用SSS[18]一维流体动力学程序分别对铝电极和不同厚度样品的速度曲线进行了模拟计算, 结果见图 9。由图 9可知, 模拟计算过程能很好地再现实验结果, 其中纯铝电极速度响应的模拟计算结果与实验结果重合较好, 归因于纯铝和LiF窗口精确的模型参数。HTPB不同厚度样品模拟计算结果能很好地反映实验过程中HTPB的响应特性, 特别是由于样品与LiF之间过大的阻抗失配(1:8.7) 造成的对HTPB的再加载, 其速度上升过程中的明显速度拐折在模拟结果中得到再现。
|
图 8 CQ-4-Shot-293实验计算模型 Fig.8 Simulation model of CQ-4-Shot-293 |
| 表 2 模拟计算参数 Tab.2 Parameters used in simulation |
|
图 9 一维模拟计算与实验结果对比 Fig.9 The comparison of one dimensional simulation results and experimental results |
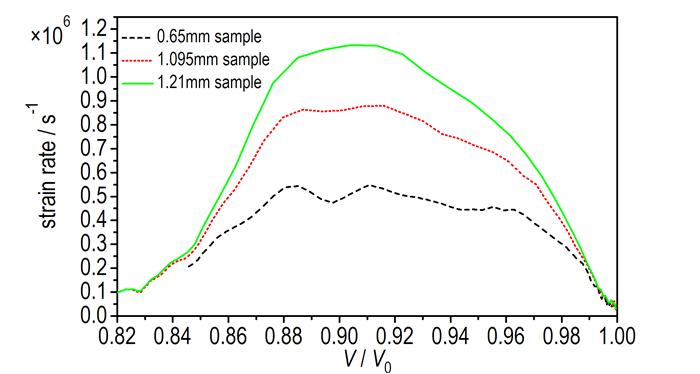
模拟计算结果中提取了3种不同厚度样品加载过程中的应变率曲线见图 10所示, 样品加载应变率为2×105~1×106 s-1, 由于应力波的追赶效应, 不同厚度样品应变率存在差异, 随着样品厚度增加, 加载应变率随之增加。由于不同厚度样品应变率无量级差异, 不能判断HTPB是否存在应变率效应, 但与文献中冲击加载实验结果对比, 可见应变率效应不明显。
|
图 10 不同厚度样品应变率与比容关系 Fig.10 The strain rate vs. specific volume curve of samples in different thickness |
针对TDI固化的HTPB样品, 利用磁驱动斜波压缩动载实验技术, 开展了斜波加载下HTPB的动力学响应实验研究, 获得了如下结果:
(1) 获得了HTPB样品在斜波加载下的速度响应曲线, 数据分析处理得到了声速与-粒子速度曲线, 其拉格朗日声速表现为线性行为, 与冲击实验文献结果一致。
(2) 实验数据分析获得了HTPB在0~1.2 GPa压力范围内的Hugoniot关系为us=1.63+2.64up, 基于该关系, 一维流体动力学模拟计算能很好地再现实验结果。
(3) 实验的应变率范围为2×105 ~1×106 s-1, 随着样品厚度增加, 加载应变率随之增加, 实验结果未见明显应变率效应。更高加载压力范围内HTPB的动力学响应是否表现出非线性行为, 尚需进一步开展实验验证。
| [1] |
王玉峰, 李高春, 刘著卿, 等. 应变率和加载方式对HTPB推进剂力学性能及耗散特性的影响[J].
含能材料, 2010, 18(4): 377-384. WANG Yu-feng, LI Gao-chun, LIU Zhu-qing, et al. Effect of strain rate and loading on mechanical properties and dissipated energy for HTPB propellant[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2010, 18(4): 377-384. |
| [2] |
赖建伟, 常新龙, 龙兵, 等. HTPB推进剂的低温力学性能[J].
火炸药学报, 2012, 35(3): 80-83. LAI Jian-wei, CHANG Xing-long, LONG Bing, et al. Low temperature mechanical properties of HTPB propellant[J]. Chinese Journal of Explosives & Propellants, 2012, 35(3): 80-83. |
| [3] |
李金飞, 黄卫东, 李高春, 等. 振动载荷对定应变HTPB推进剂力学性能影响[J].
推进技术, 2016(2): 372-377. LI Jin-fei, HUANG Wei-dong, LI Gao-chun, et al. Effects of vibration load on mechanical properties of HTPB propellant with constant strain[J]. Journal of Propulsion Technology, 2016(2): 372-377. |
| [4] |
黄辉, 董海山. 一类对撞击不敏感的新型炸药[J].
含能材料, 2002, 10(2): 74-77. HUANG Hui, DONG Hai-shan. Studies on new explosives insensitive to impact[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2002, 10(2): 74-77. |
| [5] |
马平, 李建民, 杨荣杰. HTPB基PBX的模量与撞击感度的关系[J].
火炸药学报, 2006, 29(4): 58-60. MA Ping, LI Jian-min, YANG Rong-jie. Relationship between the impact sensitivity and modulus of HTPB-based PBX[J]. Chinese Journal of Explosives & Propellants, 2006, 29(4): 58-60. |
| [6] |
贺传兰, 兰林钢, 温茂萍, 等. HTPB热固PBX老化过程中的体积收缩[J].
火炸药学报, 2014, 37(5): 20-24. HE Chuan-lan, LAN Lin-gang, WEN Mao-ping, et al. Volume shrinkage of HTPB thermosetting PBX in the aging process[J]. Chinese Journal of Explosives & Propellants, 2014, 37(5): 20-24. |
| [7] | Gupta S C, Gupta Y M. High strain rate response of an elastomer[J]. High Pressure Reseach, 1992, 10(10): 785-789. |
| [8] | Millett J C F, Bourne N K, Akhavan J. The response of hydroxy-terminated polybutadiene to one-dimensional shock loading[J]. Journal of Applied Physics, 2004, 95(9): 4722-4727. DOI:10.1063/1.1689758 |
| [9] | Hall C A, Baer M R, Gustavsen R L, et al. A study of polymer materials subjected to isentropic compression loading[C]//Shock Compression of Condensed Matter, AIP Press, 2005, 845(1): 1311-1314. |
| [10] | Wang G J, Luo B Q, Zhang X P, et al. A 4 MA 500 ns pulsed power generator CQ-4 for characterization of material behaviors under ramp wave loading[J]. Review of Scientific Instruments, 2013, 84(1): 015117 DOI:10.1063/1.4788935 |
| [11] |
蔡进涛, 赵锋, 王桂吉, 等. HMX基PBX炸药的等熵压缩实验研究[J].
含能材料, 2014, 22(2): 210-214. CAI Jin-tao, ZHAO Feng, WANG Gui-ji, et al. Quasi-isentropic compression of HMX based PBX explosive[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2014, 22(2): 210-214. |
| [12] |
蔡进涛, 王桂吉, 张红平, 等. 准等熵压缩下氟橡胶F2311的动力学行为实验研究[J].
高压物理学报, 2015, 29(1): 42-46. CAI Jin-tao, WANG Gui-ji, ZHANG Hong-ping. Mechanicalresponse of fluorine rubble F2311 under quasi-isentropic compression[J]. Chinese Journal of High Pressure Physics, 2015, 29(1): 42-46. DOI:10.11858/gywlxb.2015.01.007 |
| [13] |
赵万广, 周显明, 李加波, 等. LiF单晶的高压折射率及窗口速度的修正[J].
高压物理学报, 2014, 28(5): 571-576. ZHAO Wan-guang, ZHOU Xian-ming, LI Jia-bo, et al. Refractive index of LiF single crystal at high pressure and its window correction[J]. Chinese Journal of High Pressure Physics, 2014, 28(5): 571-576. DOI:10.11858/gywlxb.2014.05.010 |
| [14] | Vogler T J, Ao T, Asay J R. High-pressure strength of aluminum under quasi-isentropic loading[J]. International Journal of Plasticity, 2009, 25(4): 671-694. DOI:10.1016/j.ijplas.2008.12.003 |
| [15] | Reisman D B, Forbes J W, Tarver C M, et al. Isentropic Compression of High Explosives with the Z Accelerator[C]//Proceedings of the 12th International Detonation Symposium. SanDiego, CA. 2002: 343-348. |
| [16] | Hare D E. How to Plan and Analyze an Isentropic Compression Experiment (ICE)[R]. Lawrence Livermore National Laboratory Report: UCRL-TR-206486, 2004. |
| [17] | Hayes D B. Backward Integration of the Equations of Motion to Correct for Free Surface Perturbations[R]. Sandia National Laboratories Report: SAND2001-1440, 2001. |
| [18] |
孙承纬. 一维冲击波和爆轰波计算程序SSS[J].
计算物理, 1986(2): 18-30. SUN Cheng-wei. SSS: A code for computing one dimensional shock and detonation wave propagation[J]. Chinese Journal of Computation Physics, 1986(2): 18-30. |
| [19] |
汤文辉, 张若棋.
物态方程理论及计算概论[M]. 2007: 293.
TANG Wen-hui, ZHANG Ruo-qi. Introduction to theory and computation of equations of state[M]. 2007: 293. |
The dynamic response of hydroxyl-terminated polybutadiene(HTPB) samples solidified by toluene diisocynate (TDI) were investigated under ramp loading up to 1.2 GPa. The velocity response curves of three HTPB samples with different thickness were obtained by Photonic Doppler Velocimeter(PDV). The sound velocity vs. particle velocity curves and stress vs. specific volume curves were obtained by Lagrange analysis method.




