六硝基茋(HNS-Ⅳ)炸药具有良好的安全性、热安定性以及冲击起爆性能, 常作为二级装药应用于冲击片雷管和微机电系统(MEMS)微装药器件中。研究HNS-Ⅳ在冲击条件下的爆轰性能, 对火工品的设计具有重要的指导意义[1]。1981年Schwarz[2]利用爆炸箔起爆器对密度为1.6 g·cm-3 HNS-SF的临界起爆速度进行了测试, 并确定了其判据形式为p2.06τ>K(0.01 μs<τ<0.1 μs, 3.8 GPa<p<9.8 GPa)。2011年Bowden等[3]对脉冲持续时间τ的计算公式进行了修正, 并结合Schwarz的计算结果拟合得到了HNS的James判据形式0.2042/Σ+0.0879/E=1。2015年郭俊峰等[4]结合Schwarz和Bowden的数据, 拟合得到了HNS-Ⅳ冲击起爆判据p2.06τ=1.26 GPa2.06·μs (0.0016 μs<τ<0.1 μs, 3.8 GPa<p<27.1 GPa)。
目前关于HNS-Ⅳ炸药冲击起爆判据适用范围的研究较少, 对于利用数值仿真软件研究炸药冲击起爆判据的报道也较少。本研究结合Schwarz测试所得的速度阈值数据[2]对p-τ判据、James判据和Π-τ判据分别进行拟合。利用AUTODYN软件模拟了不同厚度的聚酰亚胺飞片冲击起爆HNS-Ⅳ的速度阈值, 对速度阈值的模拟值和实验值之间存在的偏差进行了讨论。同时按照p-τ判据、James判据和Π-τ判据进行了曲线拟合, 对比模拟数据和实验数据所拟合的曲线, 探究了飞片冲击起爆模型研究HNS-Ⅳ一维冲击起爆的可行性。
2 HNS-Ⅳ的冲击起爆判据1969年Waller等[5]首次提出了经典刺激量起爆判据:
| $ K = {p^n}\tau $ | (1) |
式中, p为冲击入射的压力, GPa; τ为脉冲持续时间, μs, 在特定的炸药和压力范围内n和K为常数。τ的表达式[1]为:
| $ \tau = \frac{{2d}}{{{C_{\rm{f}}} + a({V_{\rm{f}}} - {U_p})}} $ | (2) |
式中, d为飞片厚度, μm; Up为飞片中质点速度, km·s-1; Vf为飞片速度, km·s-1; Cf为飞片中声速, km·s-1; a为飞片材料的线性系数。
1996年James[6]在Waller等研究的基础上, 提出以质点比动能Σ来表征炸药内部冲击波阵面上质点的动能, 可以反映出炸药爆轰成长过程, 并提出了James判据:
| $ \frac{{{E_{\rm{c}}}}}{E}{\rm{ }} + {\rm{ }}\frac{{{\mathit{\Sigma} _{\rm{c}}}}}{{\mathit{\Sigma}}} = 1 $ | (3) |
式中, E为能量密度, MJ·m-2; Σ为质点比动能, MJ·kg, 在特定的炸药中Ec和Σc为常数。质点比动能Σ和能量密度E的表达式[6]为:
| $ \mathit{\Sigma}=\frac{{U_p^2}}{2} $ | (4) |
| $ E = p{U_p}\tau $ | (5) |
2016年Kim等[7]的研究表明, 功率通量Π可以表征冲击过程中加载面单位面积的输入速率, 因此提出了以功率通量Π和脉冲持续时间τ共同界定的Π-τ判据:
| $ \mathit{\Pi} = {\mathit{\Pi} _{\rm{c}}}\left( {1 + \frac{{{E_{\rm{c}}}/{\mathit{\Pi} _{\rm{c}}}}}{{\tau }}} \right) $ | (6) |
式中, Π为功率通量, GW·cm-2; Πc为临界功率通量, 在特定的炸药中为常数。Π的表达式[7]为:
| $ \mathit{\Pi}=p{U_p} $ | (7) |
本研究在计算过程中所用参数取值为: ρf= 1.42 g·cm-3[8], ρe=1.6 g·cm-3[9], Cf=2.737 km·s-1[8], Ce=2.2 km·s-1[9], a=1.41[8], b=1.45[9]。本研究对冲击入射压力和脉冲持续时间的计算结果与文献[2]的对比结果见表 1。由表 1可知, 对于冲击入射压力和脉冲持续时间, 本文计算值与文献值相差不大, 说明了参数选择的合理性。
| 表 1 冲击压力p和脉冲持续时间τ的计算值与文献值的对比 Tab.1 Comparison of the calculation results with literature ones for shock pressure and pulse duration time |
表 2为在不同厚度的聚酰亚胺飞片冲击起爆HNS-Ⅳ的速度阈值[2]的基础上, 按照式(1)~式(7)计算p、τ、E、Σ、Π, 并分别按照p-τ判据、Π-τ判据和James判据进行拟合, 拟合曲线如图 1所示。由图 1可知, 三种拟合曲线中Π-τ判据的拟合度最高为0.9950, James判据的拟合度最低为0.8753, 说明相比于James判据和p-τ判据, Π-τ判据更适用于文献[2]实验数据。
| 表 2 Schwarz实验速度阈值经计算得到的不同参数值 Tab.2 The values of different parameters obtained by calculation using Schwarz experimental velocity threshold data |
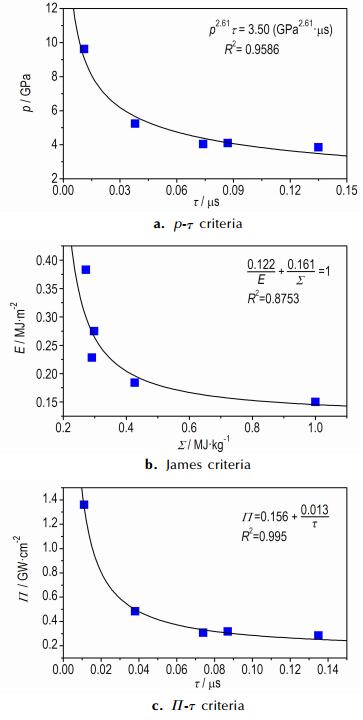
|
图 1 三种不同判据的拟合情况 Fig.1 The fitting situations of three different criteria |
以1.6 g·cm-3的HNS-Ⅳ为研究对象, 采用非线性有限元计算软件AUTODYN, 通过Lee-Taver点火增长模型, 对飞片冲击起爆HNS-Ⅳ过程进行数值模拟。图 2所示为计算所用的模型图, 整个模型由飞片、炸药和空气域所组成, 其中飞片采用Lagrange算法, 炸药和空气采用Euler算法, Lagrange算法和Euler算法之间采用流固耦合进行相互作用[10]。为了便于观测炸药内部压力变化, 沿着装药轴线方向每隔0.3 mm设置一个观测点, 共设置了7个观测点。
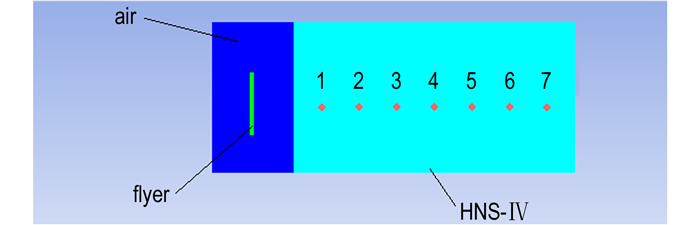
|
图 2 飞片冲击起爆HNS-Ⅳ仿真模型 Fig.2 The simulation model of initiating HNS-Ⅳ by flyer impact |
聚酰亚胺飞片采用冲击状态方程进行模拟, 参数由文献[8]提供, 其中ρ=1.42 g·cm-3, s=1.41, C=2.737 km·s-1。
HNS-Ⅳ炸药采用三项式点火与增长反应模型。该模型由未反应炸药JWL状态方程、爆轰产物的JWL方程和三项式点火增长反应速度方程来描述。未反应炸药JWL状态方程和爆轰产物状态方程[10]为:
| $ p = A{{\rm{e}}^{ - {R_1}V}} + B{{\rm{e}}^{ - {R_2}V}} + w{C_{\rm{v}}}T $ | (8) |
式中, V是相对比容; T为温度, K; w为Gruneisen系数; Cv为平均热容, 105 MPa·K-1; A、B、R1、R2是待定参数。
点火-燃烧-快反应三项式点火增长反应速率方程[11]为:
| $ \begin{array}{l} {\rm{d}}\lambda /{\rm{d}}t = {\rm{ }}I{\rm{ }}{(1 - \lambda )^b}{\left( {\rho /{\rho _0} - 1 - a} \right)^x} + {G_1}{\left( {1 - \lambda } \right)^c}{F^d}{P^y} + \\ {G_2}{\left( {1 - \lambda } \right)^e}{\lambda ^g}{P^z} \end{array} $ | (9) |
式中, λ为炸药的反应度; t为时间, μs; ρ为密度, g·cm-3; ρ0为初始密度, g·cm-3; I, G1, G2, a, b, x, c, d, y, e, g和z是常数, HNS-Ⅳ的点火与增长反应模型参数来源于文献[8]。
3.3 HNS-Ⅳ临界起爆速度的判定相关研究表明, 在研究飞片冲击起爆HNS-Ⅳ作用过程中, 可以用飞片速度来表征HNS-Ⅳ炸药的起爆阈值[1]。结合文献[2]所报道的飞片尺寸, 利用升降法不断调整飞片撞击HNS-Ⅳ时的速度, 通过观测炸药内部压力变化来判定炸药是否发生爆轰, 来获得不同厚度聚酰亚胺起爆HNS-Ⅳ的速度阈值。
如图 3所示的是Φ1.57 mm×140 μm尺寸聚酰亚胺飞片, 分别在1450 m·s-1和1460 m·s-1的速度下撞击HNS-Ⅳ, 各观测点的压力变化情况。由图 3可知, 当飞片以1450 m·s-1速度冲击HNS-Ⅳ时, 压力从初始的5.94 GPa开始升高, 达到9.85 GPa后开始不断下降, 由此说明飞片在1450 m·s-1速度下冲击HNS-Ⅳ没有形成稳定的爆轰, 炸药没有被起爆。当飞片以1460 m·s-1速度冲击HNS-Ⅳ时, 炸药内部压力从初始的6.12 GPa开始逐渐增大, 在0.47 μs时压力为20.2 GPa, 超过了HNS-Ⅳ的C-J压力, 且压力不断升高, 表明炸药内部发生了稳定的爆轰。由此可以说明1460 m·s-1是Φ1.57 mm×140 μm的聚酰亚胺飞片冲击起爆HNS-Ⅳ的阈值速度, 相比于实验值[2](1510 m·s-1)相差3.3%左右, 说明了仿真参数的合理性。
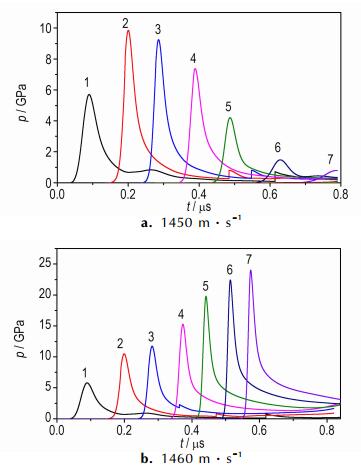
|
图 3 飞片以不同速度冲击时的压力变化情况 Fig.3 The change situation of pressure during flyer impact with different velocity |
模拟了不同厚度的聚酰亚胺飞片冲击起爆HNS-Ⅳ的速度阈值, 并与文献[2]中的实验数据进行对比, 结果见表 3, 数值模型中飞片直径均为1.57 mm。由表 3可知, 随着飞片厚度的增大, 速度阈值下降; 当飞片厚度超过140 μm时, 速度阈值变化缓慢。这主要是因为随着飞片厚度的增大, 脉冲持续时间增大, 此时炸药所需要的起爆压力减小, 因而速度阈值下降; 随着飞片厚度的进一步增大, 脉冲持续时间的增大对起爆压力变化的幅度减小, 因而速度阈值下降缓慢。
| 表 3 不同厚度的聚酰亚胺飞片起爆速度阈值变化情况 Tab.3 The change situation of initiation velocity threshold of polyimide flyer with different thickness |
由表 3可知, 实验的速度阈值和模拟速度阈值存在一定的偏差。为了研究产生偏差的原因, 根据文献[2]实际所使用的爆炸箔起爆器进行建模, 对桥箔电爆炸驱动飞片加速过程进行数值模拟, 研究了爆炸箔分别驱动25, 76, 140, 165 μm和254 μm飞片时, 飞片形态和厚度的变化。由于其余厚度(76, 140, 165 μm和254 μm)飞片的形态和厚度变化与25 μm飞片情况相似, 为了避免重复赘述, 因此只对25 μm飞片进行具体分析。
图 4所示的是25 μm的聚酰亚胺飞片在驱动过程中形态的变化情况。由图 4可见, 当t=0.03 μs时, 飞片被加速膛剪切完成, 形成一维平板状飞片在加速膛中加速; 当t=0.186 μs时, 飞片恰好从加速膛中飞出, 可以发现飞片靠近加速膛孔径一侧发生了一定的弯曲。这主要是因为数值模型中爆炸箔桥区宽度和加速膛孔径尺寸一致, 使得飞片能够均匀受力, 从而在初始阶段被剪切出平板状飞片, 与文献[12]中所描述的情况一致; 随着飞片在加速膛中的飞行, 等离子体压力降低, 加速膛内孔阻力对于飞片形态的影响逐渐出现, 飞片受到了非均匀力作用, 造成了飞片形态发生变化, 与文献[13]观点一致。
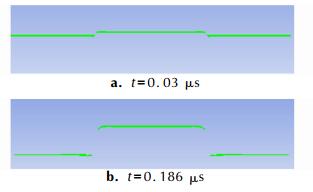
|
图 4 25 μm飞片在加速膛中加速时飞片形态 Fig.4 The flyer shapes in accelerating chamber of 25 μm flyer |
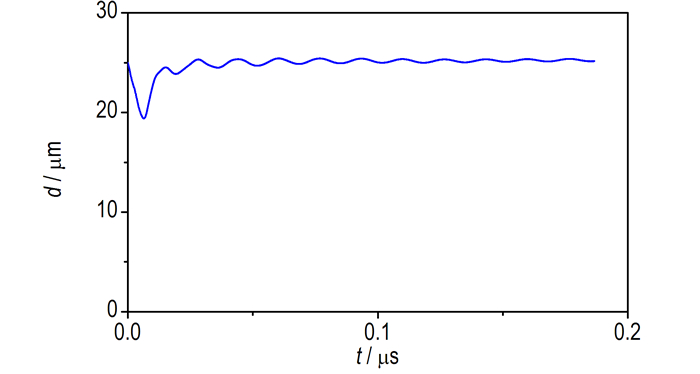
25 μm的聚酰亚胺飞片在驱动过程中厚度的变化情况如图 5所示。由图 5可知, 飞片厚度从开始被等离子体驱动到撞击炸药为止, 厚度发生了动态变化, 当t=0.009 μs时厚度最小。这是因为聚酰亚胺飞片属于有机材料, 在驱动过程中存在一个材料的动态响应过程。在冲击压缩波作用下, 飞片发生塑形变化, 厚度逐渐减小至19.4 μm; 当冲击波达到飞片自由面时, 飞片在反射形成的稀疏波作用下回弹, 厚度又逐渐增大, 与文献[13]的观点一致。
|
图 5 驱动25 μm飞片加速过程中厚度的变化 Fig.5 The change in thickness during the acceleration process of 25 μm flyer |
飞片形态的变化导致撞击炸药时发生能量侧向耗散, 影响热点集聚[12];飞片厚度的变化影响了撞击炸药时的作用面积, 从而影响热点数量变化[13]。根据本文对于爆炸箔驱动飞片过程的数值模拟研究可知, 由于飞片形态和厚度的变化, 使得实验数据和模拟数据存在一定的偏差。
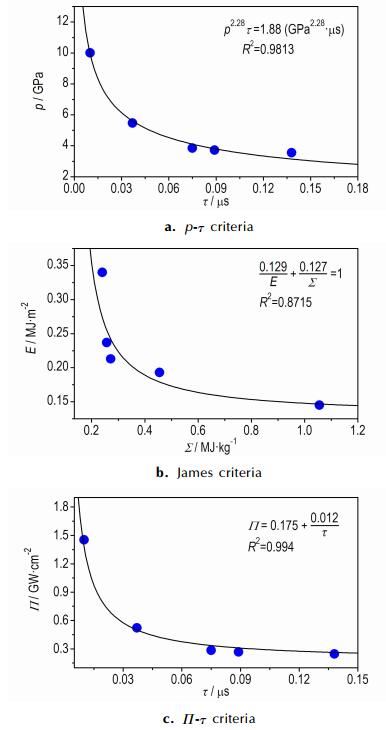
4.2 HNS-Ⅳ冲击起爆判据的模拟结果表 4所示的是根据模拟得到的速度阈值经计算所得的不同参数, 并按照p-τ判据、Π-τ判据和James判据进行拟合, 结果如图 6所示。
| 表 4 模拟的速度阈值经计算得到的不同参数值 Tab.4 The values of different parameters obtained by calculation using the simulation velocity threshold |
|
图 6 三种不同判据的拟合情况 Fig.6 The fitting situations obtained by three different criteria |
由图 6可知, 三种判据中Π-τ判据的拟合效果最佳, 而James判据拟合效果最低。这主要是因为数值模拟中采用的是平板型飞片, 属于一维冲击起爆。James判据主要是建立在弯曲飞片冲击起爆的基础上, 因而对于弯曲飞片冲击起爆的解释更为合适, 对于一维冲击起爆解释尚显不足; p-τ判据在脉冲时间较小的情况下契合度较高, 随着脉冲时间的增大, 契合度降低, 故p-τ判据更适合一维短脉冲起爆; Π-τ判据的方程形式上与p-τ判据相似, 从本研究拟合情况来看, 其对于一维冲击起爆适用性更好。
4.3 HNS-Ⅳ冲击起爆判据的讨论表 5所示是文献数据[2]和模拟数据依照三种判据形式所拟合得到的曲线方程及拟合度情况。由表 5可知, 文献实验数据的拟合结果和模拟数据的拟合结果均表明Π-τ的拟合情况最佳。实验数据和模拟数据拟合的Π-τ曲线对比情况如图 7所示。由图 7可见, 两条曲线基本重合, 说明了通过平板飞片冲击起爆HNS-Ⅳ数值模型来研究HNS-Ⅳ一维冲击起爆问题是可行的。
| 表 5 不同判据曲线拟合结果 Tab.5 The results of fitting curves using different criteria |

|
图 7 实验速度阈值和模拟速度阈值拟合的Π-τ曲线对比情况 Fig.7 Comparison of the Π-τ curves obtained by fitting the experimental and simulated velocity threshold |
(1) 利用AUTODYN软件能够模拟聚酰亚胺飞片冲击起爆HNS-Ⅳ这一过程, 仿真结果与实验研究结果一致性较好, 说明仿真结果真实可靠。
(2) 随着飞片厚度的增加, HNS-Ⅳ炸药的速度阈值降低; 当飞片厚度超过140 μm后, 速度阈值变化缓慢。说明了当飞片厚度超过一定程度后, 脉冲持续时间的影响程度减弱。
(3) 在电爆炸驱动过程中, 飞片受加速膛内孔阻力影响会发生一定的弯曲, 受材料动态响应影响飞片厚度会发生变化。
(4) 对实验速度阈值依照p-τ判据、James判据和Π-τ判据进行拟合, 结果表明采用Π-τ判据对HNS-Ⅳ一维冲击起爆研究更合适, 数值模拟结果与文献结果一致。
(5) 实验速度阈值和模拟速度阈值分别按照Π-τ判据进行拟合, 所得曲线基本重合, 说明了通过飞片冲击起爆HNS-Ⅳ模型研究HNS-Ⅳ一维冲击起爆是可行的。
| [1] |
同红海, 奥成刚, 韩克华, 等. 超细HNS-Ⅳ炸药的窄脉冲起爆判据研究[J].
火工品, 2011(2): 32-36. TONG Hong-hai, AO Cheng-gang, HAN Ke-hua, et al. Study on the short pulse initiation criterion of ultrafine HNS-Ⅳ explosive[J]. Initiators & Pyrotechnics, 2011(2): 32-36. |
| [2] |
Schwarz A C. Study of factors which influence the shock initiation sensitivity of Hexanitrostilbene (HNS)[R]. Sandia National Labs, 1981.
|
| [3] |
Bowden M D. Determination of critical energy criteria for Hexanitrostilbene using laser-driven flyer plates[J].
Proceedings of SPIE-The International Society for Optical Engineering, 2008, 7070: 707004-707004. |
| [4] |
郭俊峰, 曾庆轩, 李明愉, 等. 叠氮化铜驱动飞片起爆HNS-Ⅳ的研究[J].
火工品, 2015(6): 1-4. GUO Jun-feng, ZENG Qing-xuan, LI Ming-yu, et al. Study on HNS-Ⅳ initiation by flyer driven by cupric azide[J]. Initiators & Pyrotechnics, 2015(6): 1-4. |
| [5] |
Walker F E, Wasley R J. Critical energy for shock initiation of Heterogeneous explosive[J].
Explosivestoffe, 1969, 17(1): 9 |
| [6] |
James H R. An extension to the critical energy criterion used to predict shock initiation thresholds[J].
Propellants, Explosives, Pyrotechnics, 1996, 21: 8-13. DOI:10.1002/(ISSN)1521-4087 |
| [7] |
Kim S, Miller C, Horie Y, et al. Computational prediction of probabilistic ignition threshold of pressed granular octahydro-1, 3, 5, 7-tetranitro-1, 2, 3, 5-tetrazocine (HMX) under shock loading[J].
Journal of Applied Physics, 2016, 120(11): 734-744. |
| [8] |
Tarver C M, Chidester S K. Ignition and growth modeling of short pulse shock initiation experiments on fine particle Hexanitrostilbene(HNS)[J].
Journal of Physics:Conference Series, 2014, 500(5): 52044-52049. DOI:10.1088/1742-6596/500/5/052044 |
| [9] |
Ebenhoch S, Nau S, Haring I. Validated model-based simulation tool for design optimization of exploding foil initiators[J].
Journal of Defense Modeling & Simulation, 2014, 12(2): 189-207. |
| [10] |
仇裕成, 王健, 同红海. 钝感HNS-Ⅳ炸药飞片冲击起爆数值仿真[J].
兵工自动化, 2017, 36(3): 59-62, 65. QIU Yu-cheng, WANG Jian, TONG Hong-hai. Numerical simulation of flyer impacting initiation insensitive explosive HNS-Ⅳ[J]. Ordnance Industry Automation, 2017, 36(3): 59-62, 65. |
| [11] |
Tarver C M, Hallquist J O, Erickson L M. Modeling short pulse duration shock initiation of solid explosives[C]//8th international Symposium on detonation, Albuquerque: 1985.
|
| [12] |
张玉若, 金丽, 高艳, 等. 爆炸箔特征参数匹配关系研究[J].
火工品, 2011(1): 20-22. ZHANG Yu-ruo, JIN Li, GAO Yan, et al. Study on matching relationship of characteristic parameter of exploding foil[J]. Initiators & Pyrotechnics, 2011(1): 20-22. |
| [13] |
陈清畴. 冲击片雷管作用特征及影响规律研究[D]. 北京: 北京理工大学, 2016.
CHEN Qing-chou. Function characteristic and influence of exploding foil initiators[D]. Beijing: Beijing Institute of Technology, 2016. |

The initiation of HNS-Ⅳ explosive is achieved by giving the flyer velocity. In this way, different initiation criteria such as p-τ criterion, James criterion and Π-τ criterion are studied.




