1 引言

高聚物粘结炸药(PBX)是由颗粒性主体炸药(如HMX)和高聚物粘结剂、增塑剂、钝感剂等经一定工艺压制而成^[1-2], 如PBX-9502炸药是95%的TATB晶粒与5%的粘结剂Kel-F800组成的复合材料^[4]。最近几十年, 由于低速撞击下结构安全性和可靠性受到政府与工程界的高度重视, PBX炸药的破坏问题也备受学术界关注^[5-12]。

通常认为低速撞击下炸药的点火机制包括:弹塑性或粘弹塑性变形、损伤与破坏、裂纹萌生与发展、塑性功局域化及塑性功转化为热、热传导等^[13]。从试验观察发现, 含能材料的塑性变形与后继开裂问题, 直接影响了反应演化(如增加表面积会加速燃烧率)以及响应等级^[14]; 材料内部的非均质损伤对炸药的力学性能及感度影响很大, 裂纹扩展也将直接影响到结构完整性^[15-16]。因此, 研究PBX的裂纹产生及扩展, 对正确认识这种材料对机械刺激的响应非常必要, 同时也为评估裂纹发生的风险、研发裂纹抑制技术等提供理论支撑。

材料力学性能试验表明, 不同应力状态下PBX表现出不同的力学特性^[17-19], 这给数值建模带来很大的困难^[20-22]。本研究采用应力状态相关的强度模型、非关联流动法则, 描述材料在复杂应力状态下的非线性本构行为。同时, PBX在破坏模式方面表现出脆性/准脆性特点, 这种材料即使整体上承受压缩载荷, 但由于材料内部存在非均质(如微孔洞)特性^[23-24], 在外部压应力作用下, 材料内部微孔洞附近产生局部的拉伸裂纹, 随着载荷发展微裂纹进一步演化、扩展, 最终导致材料或结构的整体破坏^[25-27]。在模拟PBX脆性拉伸裂纹行为方面, 通常方法有:连续介质损伤力学的数值模拟方法^[28-29]、直接数值模拟方法^[30]、以及多尺度^[31]或细观数值模拟方法^[32], 以及扩展有限元(XFEM)^[33-37]。由于XFEM在模拟裂纹时无需对齐网格、裂纹扩展计算时无需重新划分网格等优点, 目前备受学术界关注。本研究利用XFEM方法, 针对PBX带孔板压缩破坏试验^[26], 分析PBX-9502炸药的启裂与扩展, 在材料损伤与破坏方面, 采用cohesive模型。

2 XFEM基本思想

XFEM是一种解决断裂力学问题的新的有限元方法, 首先由Belytschko和Black^[38]提出, 该方法基于单位分解^[39], 将常规有限元法进行了扩展, 采用独立于网格剖分的思想解决有限元中的裂纹扩展问题, 在保留传统有限元所有优点的同时, 并不需要对结构内部存在的裂纹等缺陷进行网格划分。XFEM是迄今为止求解不连续问题最有效的数值方法, 它在标准有限元框架内研究问题, 保留了有限元方法的所有优点, 因此XFEM成为目前裂纹扩展模拟的主要方法之一, 也代表了计算力学数值方法近十多年来的主要进展。XFEM在处理裂纹时, 无需对齐网格, 裂纹扩展也无需重新划分网格, 而且稀疏网格也可以得到高精度数值解。XFEM这些优点使得这一方法在近十多年的计算力学界十分活跃^{[33, 35]}。

在分析断裂问题中, XFEM引入强化基函数, 包括:裂尖附近渐进函数, 以刻画裂尖附近的应力奇异性; 不连续函数, 以表征跨越裂纹面的位移跳跃。本研究在裂纹张开与移动的计算中, 采用内聚力模型^[40]和虚拟节点方法^[41-42], 即在XFEM方法的框架中, 引入单元材料的拉伸-分离的内聚行为, 以模拟裂纹的萌生及扩展过程。在材料破坏方面, 采用内聚力方法; 在裂纹行为方法, 基于XFEM模拟方法, 这样结合起来, 可以模拟材料内裂纹产生及沿任意路径分析的扩展过程, 而且裂纹扩展并不必强制沿着单元边界。

3 基于XFEM的内聚力模型

Cohesive模型属于损伤模型, 最先由Barenblatt^[40]引入, 使用拉伸-分离法则来模拟原子晶格的减聚力, 避免了裂纹尖端的奇异性^[43]。Cohesive模型与有限元方法结合首先被用于混凝土计算和模拟, 后来也被引入金属、陶瓷、复合材料等。Cohesive界面/单元须服从Cohesive分离法则, 包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。典型的分离法则有Needleman律^[44]、Hillerborg律^[45]、Bažant律^[46]。

本研究的裂纹扩展分析中, 采用了基于XFEM的内聚片段法, 应用了线弹性拉伸-分离模型、损伤启动准则和损伤演化律。在线弹性拉伸-分离模型中, 假设初始为线弹性行为, 后跟损伤启动与演化。线弹性行为表示为裂纹单元的内聚应力t与张开位移δ之间的线性关系, 即:

$t = K\delta $

(1)

式中:

$\begin{array}{l} t = {[{t_{\rm{n}}},{t_{\rm{s}}},{t_{\rm{t}}}]^T}\\ \delta = {[{\delta _{\rm{n}}},{\delta _{\rm{s}}},{\delta _{\rm{t}}}]^T}\\ K = {\rm{diag}}[{K_{{\rm{nn}}}},{K_{{\rm{ss}}}},{K_{{\rm{tt}}}}] \end{array}$

(2)

t_n为法向应力分量, t_n和t_t为两个切向应力分量, 相应的分离量分别为δ_n, δ_s, δ_t。法向与切向刚度分量间不存在耦合现象:纯法向分离量并不会引起切向内聚力, 纯切向滑动也不会引起法向内聚力。刚度阵中的分量K_nn, K_ss, K_tt可通过强化单元的弹性参数计算。

在模拟拉伸开裂时, 采用最大主应力准则作为启裂准则, 即当

$f=\left\{ \frac{＜{{\sigma }_{\text{max}}}＞}{\sigma _{\text{max}}^{0}} \right\}=1$

(3)

满足时, 裂纹启动(启裂)。式中σ_max⁰为最大许可主应力, ＜·＞为Macaulay括号。

采用标量损伤变量D∈[0, 1]描述内聚刚度退化率, 即损伤演化律, 以表征裂纹面与裂开单元边之间交集部分的整体平均损伤程度。在裂纹张开过程采用损伤演化方程描述, 采用能量形式的线性或指数型演化方程:

${\rm{d}}D = \frac{{T(\delta ){\rm{d}}\delta }}{{{G_{{\rm{eqC}}}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{T_{{\rm{max}}}}(1 - \delta /{\delta _{{\rm{max}}}}){\rm{d}}\delta }}{{{G_{{\rm{eqC}}}}}}}\\ {\frac{{{T_{{\rm{max}}}}{\rm{exp}}(\delta /{\delta _{{\rm{max}}}}){\rm{d}}\delta }}{{{G_{{\rm{eqC}}}}}}} \end{array}} \right.$

(4)

式中, G_eqC为等效的临界断裂能释放率, J·m^-2, 采用BK幂律模型^[47]:

${G_{{\rm{eqC}}}} = {G_{{\rm{ⅠC}}}} + ({G_{{\rm{ⅡC}}}} - {G_{{\rm{ⅠC}}}}){\left( {\frac{{{G_{{\rm{Ⅱ}}}} + {G_{Ⅲ}}}}{{{G_{Ⅰ}} + {G_{{\rm{Ⅱ}}}} + {G_{Ⅲ}}}}} \right)^n}$

(5)

受损材料后, 方程(1) 中的法向与切线应力分量表示为:

$\begin{array}{l} {t_{\rm{n}}} = (1 - D){T_{\rm{n}}}\\ {t_{\rm{s}}} = (1 - D){T_{\rm{s}}}\\ {t_{\rm{t}}} = (1 - D){T_{\rm{t}}} \end{array}$

(6)

式中, 当法向受压缩即T_n＜0时, 不产生裂纹, 即t_n=T_n。T_n、T_s和T_t分别为无损线弹性情况下预测的法向、切向应力分量。为了描述跨越界面同时存在法向与切线分离时的损伤演化, 采用有效分量:

${{\delta }_{\text{max}}}=\sqrt{＜{{\delta }_{\text{n}}}{{＞}^{2}}+\delta _{\text{s}}^{2}+\delta _{\text{t}}^{2}}$

(7)

4 复杂应力状态下PBX塑性变形描述

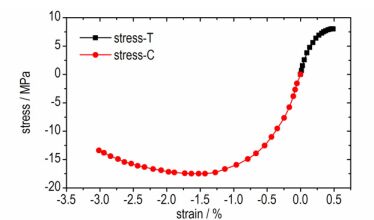
根据TATB基炸药变形特征, 如50 ℃温度下准静态拉、压不对称性^[19], 如图 1所示, 本研究采用压力相关的屈服面、非关联流动法则以及应力状态相关的拉、压加权函数, 来描述复杂应力状态下材料的力学行为, 模型中引入拉伸与压缩试验数据。

4.1 屈服面

PBX在弹性变形段, 采用线弹性本构模型描述, 假设拉压模量相同。在塑性变形阶段, 由于PBX材料为内聚摩擦材料, 围压对其力学性能有影响, 因此在屈服函数中需引入应力张量第一不变量(或流体静压)。本研究借鉴了Lubliner等人^[48]研究, 后经Lee和Fenves^[49]进行了改进, 主要考虑了拉伸与压缩下强度差异, 屈服面的演化由两个独立演化参量$\tilde \varepsilon _t^{\rm{p}}$和$\tilde \varepsilon _{\rm{c}}^{\rm{p}}$描述, 具体形式为:

$\begin{array}{l} F(\sigma ,{{\tilde \varepsilon }^{\rm{p}}}) = \frac{1}{{1 - \alpha }}[q - 3\alpha p + \beta ({{\tilde \varepsilon }^{\rm{p}}})\left\langle {{{\hat \sigma }_{{\rm{max}}}}} \right\rangle - \gamma \left\langle { - {{\hat \sigma }_{{\rm{max}}}}} \right\rangle ] - \\ \quad \quad \quad \quad {{\hat \sigma }_{\rm{c}}}({{\tilde \varepsilon }^{\rm{p}}}) = 0 \end{array}$

(8)

式中, σ为应力张量, ${{\tilde \varepsilon }^{\rm{p}}}{\rm{ = }}{\left[ {\tilde \varepsilon _t^{\rm{p}},\tilde \varepsilon _{\rm{c}}^{\rm{p}}} \right]^T}$, p=-(1/3)σ:I为流体静压; $q = \sqrt {\left( {3/2} \right)\mathcal{S}:\mathcal{S}} $为von Mises等效应力; α、β和γ为无量纲材料参数, 取为

$\begin{array}{l} \alpha = [({\sigma _{{{\rm{b}}_{\rm{0}}}}}/{\sigma _{{{\rm{c}}_{\rm{0}}}}}) - 1\left] / \right[2({\sigma _{{{\rm{b}}_{\rm{0}}}}}/{\sigma _{{{\rm{c}}_{\rm{0}}}}}) - 1],\\ \beta = [{\sigma _{\rm{c}}}(\tilde \varepsilon _{\rm{c}}^{\rm{p}})/{\sigma _{\rm{t}}}(\tilde \varepsilon _{\rm{t}}^{\rm{p}}](1 - \alpha ) - (1 + \alpha ),\\ \gamma = 3(1 - {K_{\rm{c}}})/(2{K_{\rm{c}}} - 1); \end{array}$

采用材料的摩擦角计算α=tanφ/3, 根据文献[50]中试验数据, 本研究选取20°; ${{{\hat \sigma }_{{\rm{max}}}}}$为最大主应力, (σ_b0/σ_c0)为双轴压缩与单轴压缩强度比, 借鉴内聚摩擦材料如混凝土的研究, 本研究为1.16; K_c=q_TM/q_CM为拉、压伸子午线上应力第二不变量q_TM和q_CM之比, 取2/3; ${{\sigma }_{\text{t}}}\left( \tilde{\varepsilon }_{t}^{\text{p}} \right)$和${\sigma _{\rm{c}}}(\tilde \varepsilon _{\rm{c}}^{\rm{p}})$为拉、压粘聚力, 试验测得。

4.2 流动势

与金属材料不同的是, 内聚摩擦类材料表现出剪胀特性, 需采用非关联流动法则^[51]:

${{\dot \varepsilon }^{\rm{p}}} = \dot \lambda {\nabla _{\bar \sigma }}\mathit{\Phi }\left( \sigma \right) = \dot \lambda \frac{{\partial G\left( \sigma \right)}}{{\partial \sigma }}$

(9)

$G = \sqrt {{{(e{\sigma _{{{\rm{t}}_{\rm{0}}}}}{\rm{tan}}\psi )}^2} + {q^2}} - p{\rm{tan}}\psi $

(10)

式中, ${\dot \lambda }$为非负的塑性一致性参数, 流动势函数G取Drucker-Prager双曲线函数。σ_t0为单轴拉伸破坏应力, MPa; ψ为剪胀角; e为偏心率。根据屈服函数和流动势函数, 就可获得增量本构关系^[52]:

${\rm{d}}\sigma = (C - \frac{1}{h}\nabla F \cdot C \otimes C \cdot \nabla G):{\rm{d}}\varepsilon $

(11)

式中, $h = {\nabla _\sigma }F \cdot C \cdot C \cdot {\nabla _\sigma }G - {\nabla _{{\varepsilon ^{\rm{p}}}}}F \cdot {\nabla _\sigma }G - C{f_{,k}}{f_{{\varepsilon ^{\rm{p}}}}}\sqrt {\nabla G \cdot \nabla G} $。

4.3 塑性应变演化

针对拉压异性材料的塑性应变${{\tilde \varepsilon }^{\rm{p}}}{\rm{ = }}{\left[ {\tilde \varepsilon _{\rm{t}}^{\rm{p}},\tilde \varepsilon _{\rm{c}}^{\rm{p}}} \right]^T}$的演化, 采用应力空间的距离函数r(σ)对三个主应变$\left( {{{\dot \varepsilon }_i},i = 1,2,3} \right)$进行加权处理, 应变率也是同样, 即:

${{{\dot{\tilde{\varepsilon }}}}^{\text{p}}}\text{=}\left[ \begin{matrix} \dot{\tilde{\varepsilon }}_{\text{t}}^{\text{p}} \\ \dot{\tilde{\varepsilon }}_{\text{c}}^{\text{p}} \\ \end{matrix} \right]=\hat{h}\left( \hat{\sigma },{{{\tilde{\varepsilon }}}^{\text{p}}} \right)\cdot {{{\dot{\tilde{\varepsilon }}}}^{\text{p}}}$

(12)

式中, $\hat{h}\left( \hat{\sigma },{{{\tilde{\varepsilon }}}^{\text{p}}} \right)=\left[ \begin{matrix} r\left( {\hat{\sigma }} \right)&0&0 \\ 0&0&-\left[ 1-r\left( {\hat{\sigma }} \right) \right] \\ \end{matrix} \right]$、${{{\dot{\tilde{\varepsilon }}}}^{\text{p}}}=\left[ \dot{\tilde{\varepsilon }}_{\text{1}}^{\text{p}},\dot{\tilde{\varepsilon }}_{\text{2}}^{\text{p}},\dot{\tilde{\varepsilon }}_{\text{3}}^{\text{p}} \right]$; 或者表示为$\dot{\tilde{\varepsilon }}_{\text{t}}^{\text{p}}=r\left( {\hat{\sigma }} \right)\hat{\dot{\varepsilon }}_{\text{max}}^{\text{p}}$和$\dot{\tilde{\varepsilon }}_{\text{c}}^{\text{p}}\text{=}-\left[ 1-r\left( {\hat{\sigma }} \right) \right]\hat{\dot{\varepsilon }}_{\text{min}}^{\text{p}}$。通过应变率积分获得应变, $\dot{\tilde{\varepsilon }}_{\text{t}}^{\text{p}}\text{=}\int_{0}^{t}{r\left( \sigma \right)}\hat{\dot{\varepsilon }}_{\text{max}}^{\text{p}}$。$r\left( {\hat{\sigma }} \right)$为三轴应力加权因子, 定义为:

$r\left( {\hat{\sigma }} \right)=\frac{\text{def}\sum\nolimits_{i=1}^{3}{\left\langle {{{\hat{\sigma }}}_{i}} \right\rangle }}{\sum\nolimits_{i=1}^{3}{\left| {{{\hat{\sigma }}}_{i}} \right|}}$

(13)

式中, ${{{\hat{\sigma }}}_{i}}\left( i=1,2,\cdots \right)$主应力分量, $\left\langle x \right\rangle =\frac{1}{2}\left( \left| x \right|+x \right)$为Macauley括号。可见, 当所有的主应力${{{\hat{\sigma }}}_{i}}$为正时, $r\left( {\hat{\sigma }} \right)$等于1;当主应力${{{\hat{\sigma }}}_{i}}$为负时, $r\left( {\hat{\sigma }} \right)$为0。通过这种方法, 只需要测试材料的压缩与拉伸曲线, 就可以计算复杂应力状态下的材料响应。

根据TATB钝感炸药相关试验数据^{[17, 50, 53]}, 本研究采用表 1的材料模型参数。

5 计算模型及结果分析

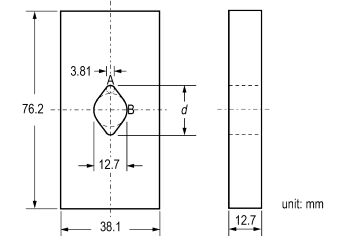
本研究采用文献[26]的试验模型。试验材料为TATB基钝感炸药, 试验温度为50 ℃, 试验采用单轴压缩加载, 加载速率为1.27 mm·min^-1。试件几何为中心带椭圆形孔板, 如图 2所示。板尺寸的高×宽×厚为76.2 mm×38.1 mm×12.7 mm, 中心孔由四段直线和两段弧线围成, 弧线段的直径为12.7 mm和3.81 mm, 孔的高度d为19.05 mm, 孔的上端顶点为A, 侧边顶点为B。数值模拟的网格为四边形平面应力单元, 单元尺寸约0.5 mm; 采用最大主应力和断裂能准则, 无需预置初始裂纹。

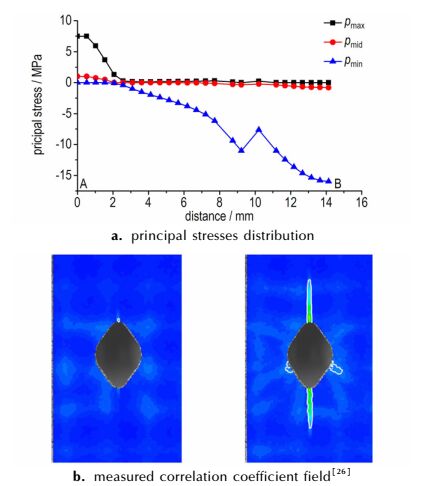
采用PANDA_Fracture进行XFEM分析, 计算结果表明, 板在整体压缩作用下, 中心孔的四周受力与变形很不均匀, 在孔的上、下两端点承受的第一主应力为拉应力, 且沿孔内壁分布为最大点。图 3a为拉伸裂纹产生前孔内壁从顶点A到侧边B点之间、沿孔内壁的主应力分布; 可见A点所受的第一主应力为最大, B点所受的第三主应力和剪应力为最大(绝对值), 因此开裂破坏模式首先在A点萌生, 裂纹方向将与最大主应力方向垂直; 其次在B点将会萌生剪切破坏模式; 从实测相关系数场图 3b中也可以证实这一结果^[26]。

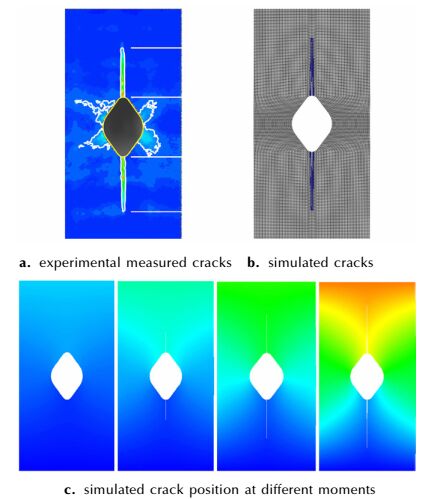
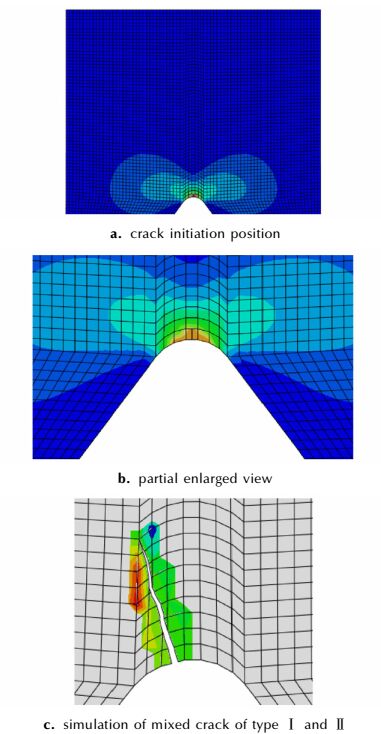
数值模拟表明, 在外部压应力作用下, 试件内部孔洞附近产生非均匀变形场与应力场, 导致应力集中或高的应力梯度, 当局部应力如拉应力到达材料破坏应力时, 产生局部的拉伸裂纹, 随着外载于变形进一步发展, 裂纹在萌生处迅速沿着最大主应力区域扩展, 最终形成两条宏观裂纹, 如图 4所示, 其中图 4a为试验图, 图 4b为数值模拟获得的裂纹最终图, 图 4c为典型时刻的裂纹位置图。图 5为数值模拟, 其中孔内壁A点的拉伸裂纹萌生及裂纹方向图像见图 5b。图 5c为混合裂纹预测图:当把端面位移载荷同时施加到纵向与横向时, 从孔内壁顶点附近产生Ⅰ-Ⅱ型混合裂纹。

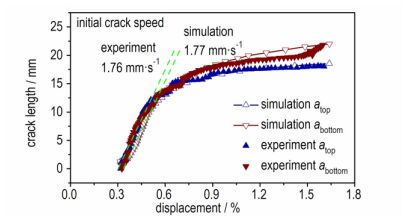
图 6为启裂时间、裂纹扩展速度、裂纹扩展历程的数值模拟结果与试验^[26]对比。整体上数值模拟给出的裂纹发展趋势与试验结果相吻合, 如上、下裂纹时程的整体走势和拐点, 启裂时刻均在δ/H=0.32%(约0.2 min), 裂纹初期扩展速度的试验值为1.76 mm·s^-1, 数值模拟值为1.77 mm·s^-1。这说明基于XFEM和内聚模型的方法, 对Ⅰ型裂纹的产生、扩展的模拟是可行的; 在裂纹产生、扩展等整体发展规律上, 数值模拟可以给出好的预测。但在一些细节上, 如裂纹产生后, 数值模拟得到的裂纹扩展较实测值有一个滞后; 且裂纹发展后期, 模拟与实测的裂纹位置有一定的偏差。可能的原因有:

(1) 试验测试裂纹位置时, 理论上需要足够高的分辨率以识别裂纹、捕捉裂尖位置, 但在实际测量中很难做到, 这可能导致裂纹位置、长度等的测试值与实际有差异。

(2) 目前采用的XFEM计算, 简化的算法导致裂纹扩展时一次性地穿越一个单元, 显式上单元内裂纹的速度为无穷大, 当网格不是足够精细时, 会导致裂纹扩展在时间预测方面有一定的误差。

(3) 在模拟裂纹间断面时材料损伤破坏导致材料软化、刚度劣化, 数值算法遇到收敛困难; 为克服这种困难, 在内聚本构模型的算法中引入表征粘性系统松弛时间的粘性系数, 进行粘性正则化处理。这也导致材料破坏模拟方面出现很小程度的松弛效应。

(4) 由于PBX炸药具有细观非均质特性, 力学参数有一定的随机分散性, 而且在加工过程中, 孔周边受到一定程度的损伤, 可能导致裂纹扩展曲线上出现局部的跳跃, 如下端曲线, 本研究的数值方法没有计及这些影响。

6 结论

(1) PBX-9502带孔板在整体压应力条件下, 孔洞周围产生非均匀应力与变形场, 导致局部应力集中; 当拉应力到达材料破坏强度时, 局部位置萌生开裂破坏模式; 随着载荷与变形的发展, 裂纹单元损伤继续演化, 当达到临界值时, 裂纹进一步张开, 沿着最大主应力区域扩展, 最终导致材料整体开裂破坏。这是含孔洞板受压开裂机理, 减小孔洞内壁或周边的拉伸应力集中的措施, 将有助于防止开裂破坏。

(2) 整体上数值模拟给出的裂纹发展趋势与试验结果相吻合, 包括裂纹时程的整体走势和拐点、启裂时刻、裂纹初期扩展速度等; 表明基于XFEM和内聚模型的方法, 对 Ⅰ型裂纹的产生、扩展的模拟是可行的; 在裂纹产生、扩展等整体发展规律上, 数值模拟可以给出较好预测。

(3) 由于PBX炸药具有细观非均质特性, 其宏观上力学参数有一定的分散性或随机性, 因此良好的数值预测需要统计试验数据作支撑, 将材料参数的统计特性引入到数值模拟中。