1 引言

低温感包覆火药装药不仅能够降低火炮装药的温度系数，而且能在不增大膛压的前提下提高火炮初速，在大中口径火炮上具有良好的弹道性能^[1]。低温感包覆火药一般由多孔发射药(基体药)及其表面上的包覆层构成。包覆层的性能直接影响了基体药的燃烧。已有的研究表明，包覆层的燃烧不遵循几何燃烧定律，在一定的压力下，基体火药孔上的包覆层在未完全燃尽时就被高压气体所贯穿，称之为破孔过程。由于点传火的不同时性及包覆层不均匀，低温感包覆火药的破孔不同时^[2]。因此，无论是用经典内弹道还是两相流方法计算其内弹道时，都必须考虑破孔过程。然而影响破孔过程的因素很多，比如包覆层的物理化学性质、点传火结构、环境温度、装填密度等，在现有的条件下很难用数值方法精确描述。

鲍廷钰建立的势平衡理论^[3-5]，以实测的膛内p-t曲线为基础，确定势平衡点，建立膛内燃烧的实际燃气生成函数，从综合、整体的角度对内弹道过程进行分析和计算，近几年来，在深钝感球扁药^[6]、变燃速发射装药^[7]、电热化学炮^[8]等新型复杂装药的计算中得到应用。

目前势平衡理论在低温感包覆火药装药中的应用研究较少。文献[1]计算了几种低温感包覆火药装药的势平衡点参数及其实际燃气生成函数，但其内弹道过程特征、具有这种特征的原因及其势平衡内弹道模型的应用等仍需要进一步的研究。基于此，本研究运用势平衡理论，分析了低温感包覆火药装药与制式装药内弹道实验中的p-t曲线，对比了两者在内弹道过程中的差异，并在此基础上对低温感包覆火药装药进行内弹道模拟计算。

2 势平衡理论分析 2.1 势平衡点的确定

势平衡点是势平衡理论中最重要的特征点。通过对势平衡点的比较分析，可以发现复杂装药膛内实际燃烧过程的特殊之处。同时势平衡点的各参数也是实际燃气生成函数拟合的基础。

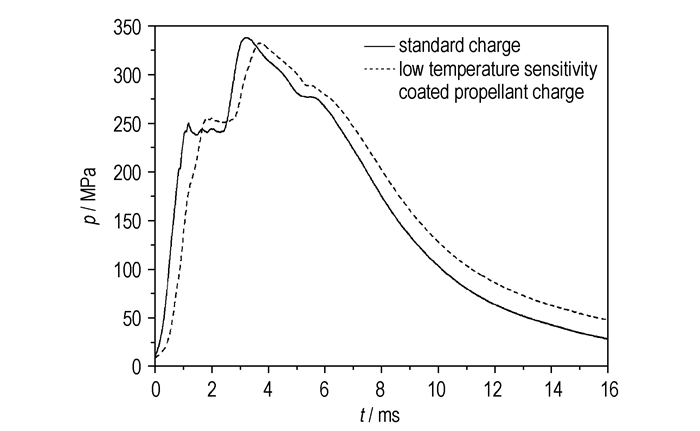
对某大口径火炮制式全装药与低温感包覆火药装药的内弹道过程进行实验研究，其p-t曲线如图 1所示。实验装药条件为：制式装药：AGU-15 22/19H;低温感包覆火药装药：主装药：AGU-15 22/19H，包覆火药：AGU-15 20/19HB, 主装药与包覆火药质量比7:3；AGU-15火药力：1070 kJ/kg, 余容：1.06×10^-3 m³/kg; 密度:1680 kg/m³；两种装药的装填密度相同。火炮条件为：某大口径火炮，药室容积：22.94×10^-3 m³，弹丸质量45.54 kg，弹丸行程全长：6.009 m，次要功系数：1.10。由图 1可见，低温感包覆火药装药p-t曲线最大压力点时间比制式装药延后，且最大压力略小。

在p-t曲线的基础上，根据态冲量J=pt、压力冲量$ I = \int_0^t {p{\rm{d}}t} $计算得到J-t曲线和I-t曲线。在势平衡点J_E=I_E，可确定势平衡点的t_E、J_E、I_E及p_E;

由公式(1)-(4)分别计算势平衡点的ψ_E、β_E、v_E、l_E

$ {\psi _E} = {\rm{ }}\frac{K}{2}\frac{{{S^2}I_E^2}}{{f\omega \;{\beta _E}\varphi m}} $

(1)

$ {\beta _E} = 1 + \left( {\alpha-\frac{1}{r}} \right){\rm{ }}\frac{{{p_E}}}{f} $

(2)

$ {v_E} = {\rm{ }}\frac{{S{I_E}}}{{\varphi m}} $

(3)

$ l{_E} = \frac{1}{2}{v_E}{t_E} + \frac{\omega }{{Sr}}-\frac{{{V_0}}}{S} $

(4)

式中，ψ为火药相对已燃部分，K为绝热指数，S为炮膛截面积，f为火药力，ω为装药质量，β为余容影响系数，φ为阻力系数，m为弹丸质量，α为余容，r为火药密度，v为弹丸速度，l为弹丸行程，t为时间，V₀为药室容积。下标E表示势平衡点参数。

由表 1可见，低温感包覆火药装药较制式装药达到势平衡点的时间和对应的弹丸行程都增加，主要原因是包覆药由于阻燃包覆层的作用，初始燃烧缓慢，总燃烧时间比制式装药长。所以，低温感包覆火药装药的火药燃烧统计平均分裂点也比制式装药向后推移，对应的势平衡理论中的特征值ψ_E的值也比制式装药大。

势平衡理论认为，对于同一批号的火药而言，其ψ_E值可以标志该批火药的燃烧特性，它仅与火药的装药结构和其形状、尺寸等有关，而与装填条件无关。表 2中三组不同装填密度的低温感包覆火药装药的装药成分是一致的，三组装药的内弹道性能正常，其势平衡点处的参数t_E、p_E、I_E、l_E、V_E、β_E的变化均在合理的范围内。但ψ_E值的变化与传统理论不相符，ψ_E值随装填密度的增加而增加。

ψ_E值变化可由低温感包覆火药装药的破孔过程来解释。由于破孔过程与装填密度相关，装填密度的改变相当于改变了达到包覆火药破孔压力的时间，即改变了包覆火药基体火药加入燃烧的时间，从而装药的燃烧规律则相应的发生改变，ψ_E值发生变化。ψ_E值随装填密度的变化间接证明了低温感包覆火药对燃气生成规律的调控。

2.2 实际燃气生成函数的计算

根据公式(5)与(6)将I-t曲线换算为v-t曲线和V-t曲线，再由公式得到ψ-I曲线，令$ \overline Z = \frac{I}{{{I_E}}} $得到$ \psi-\overline Z $曲线。

$ v = \frac{{SI}}{{\varphi m}} $

(5)

$ V = \frac{{{S^2}}}{{\varphi m}}\int_0^t {I{\rm{d}}t} $

(6)

$ \psi = \frac{{p(V + {V_0}-\frac{\omega }{r}) + \frac{1}{2}\left( {K-1} \right)\varphi m{v^2}}}{{f\omega + p\alpha \omega-p\frac{\omega }{r}}} $

(7)

以图 1中低温感包覆火药装药的p-t曲线为例进行实际燃气生成函数的拟合。

主体燃烧阶段，$ 0 \le \overline Z \le 1 $，采用四次式对$ \psi-\overline Z $曲线拟合：

$ {\psi _1} = 2.1035\overline Z (1-2.5308\overline Z + 3.5052{\overline Z ^2}-1.5694{\overline Z ^3}) $

(8)

碎粒燃烧阶段，$ \overline Z \ge 1 $，计算得到如下三次式：

$ {\psi _2} = 0.9718\overline Z (1 + 0.09973\overline Z-0.2069{\overline Z ^2}) $

(9)

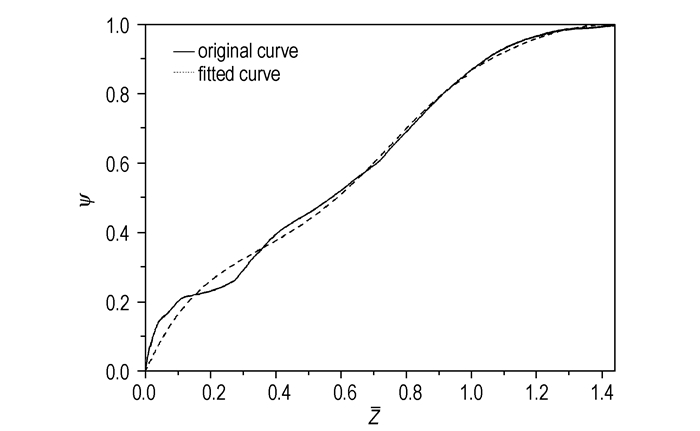
图 2为拟合曲线和原始曲线的比较。由图 2可见，除初始阶段拟合有所误差外，两条曲线基本一致。

3 势平衡内弹道模拟

在已求出的实际燃气生成函数(8)(9)的基础上，以势平衡点为标准态建立弹道相似方程组。

$ \left\{ \begin{array}{l} \overline p \overline V = K{\overline \pi _\psi }-\left( {K-1} \right){\overline Z ^2}\\ \overline p {\rm{d}}\overline V = 2\overline Z {\rm{d}}\overline Z \\ \overline t = \int\limits_0^{\overline Z } {\frac{{{\rm{d}}\overline Z }}{{\overline p }}} \end{array} \right. $

(10)

式中，$ \overline p = \frac{p}{{{p_E}}} $、$ \overline V = \frac{{V + {V_0}-\frac{\omega }{r}}}{{{V_E} + {V_0}-\frac{\omega }{r}}} $、$ \overline Z = \frac{I}{{{I_E}}} $、$ \overline t = \frac{t}{{{t_E}}} $、$ \overline \pi = \frac{{\beta \psi }}{{{\beta _E}{\psi _E}}} $

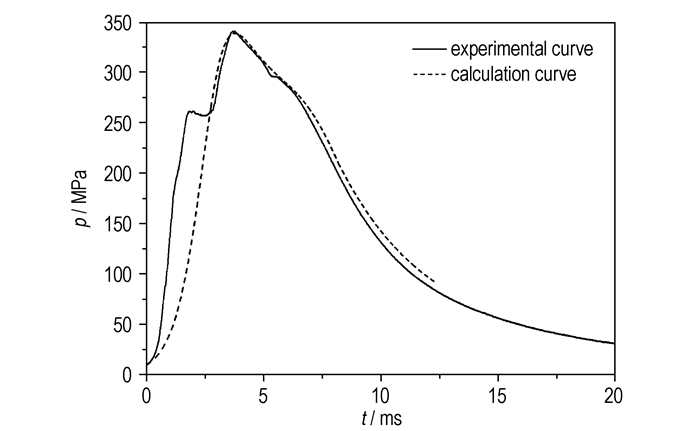
由以上弹道相似方程组结合实际燃气生成函数，便可进行内弹道计算模拟。同样对图 1中低温感包覆火药装药的p-t曲线进行模拟，利用2.2节拟合的实际燃气生成函数，计算的p-t曲线如图 3。计算值与实验曲线基本一致。

4 结论

(1) 运用内弹道势平衡理论对低温感包覆火药装药的的内弹道进行分析，可以发现，在相同的装填密度下，低温感包覆火药装药的势平衡点处ψ_E值比制式装药大；低温感包覆火药装药的的ψ_E值随装填密度的增加而增加。

(2) 由势平衡理论确定实际燃气生成函数，从而建立的弹道解法简单实用，其计算结果与实验结果基本一致。