复合固体推进剂是火箭发动机动力的直接提供者, 具有多相结构, 组分间界面分明。目前工程中常用的宏观的唯象学方法[1]仅能描述复合固体推进剂的宏观力学表象, 无法对推进剂受载过程中的内在结构变化进行有效研究, 因而从细观角度出发, 对复合固体推进剂的力学性能进行定性及定量分析将成为解决上述问题的一种有效途径。
目前常用的颗粒夹杂型复合材料的细观研究方法主要分为解析法、试验法及数值法[2]。其中细观力学解析方法因其考虑因素较少, 精度有限, 在应用上受到一定的限制。而试验法及数值法对具有复杂细观结构的复合材料有良好的适应性, 是目前工程及科学研究中解决细观力学问题的重要工具。张兴高[3]等采用电镜扫描, 并结合界面化学原理, 测得AP及HTPB粘合剂体系的接触角及表面能参数, 进而得到了界面性能与老化之间的有效关系。李高春[4]等结合电镜扫描及数字图像相关性分析, 对复合固体推进剂的细观界面脱粘进行了研究, 得到了细观结构位移场信息。Matous[5-6]结合均匀化数学理论和界面粘结模型发展了小应变下复合固体推进剂多尺度损伤模型, 计算并分析了推进剂在不同载荷条件下的损伤机理及过程。Chang等[7]采用双线性内聚力模型来反映界面的力学响应特征, 分析了细观粘接界面的损伤与失效进程, 研究了不同界面特性对力学行为的影响规律。曲凯等[8]在双线性脱粘模型的基础上, 提出了双抛物线型的界面脱粘模型, 并结合Mori-Tanaka方法对不同细观结构推进剂的宏观力学行为进行了分析研究。职世君[9]选用粘结接触来替代传统界面粘接单元以模拟界面的力学性能, 并对复合固体推进剂的细观损伤形貌进行了数值仿真研究。Kulkarni[10]等采用率无关指数型粘接单元来模拟颗粒与基体间粘接作用, 并对细观结构及粘接模型参数对界面的宏观力学行为的影响进行了分析研究。Han[11]为了更为准确的描述复合推进剂的颗粒与基体间的界面损伤, 建立了指数型的率相关粘聚区模型, 并通过实验的反演识别方法获取了相关的粘聚区参数, 并准确模拟了混合模式下HTPB推进剂的裂纹扩展过程。韦震[12]通过铝板与丁羟胶宏观粘接相关试验, 利用双线性内聚力模型表征Al/HTPB的界面属性, 并结合分步反演方法, 获取了铝与丁羟胶细观粘接界面的具体参数。
以上文献主要集中于对复合固体推进剂宏观松弛力学行为预测及细观界面参数对推进剂宏观力学行为影响的研究, 在界面单元本构的选取上, 大都选用率无关的简单模型, 而在实际固体推进剂中, 由高聚物粘合剂基体与颗粒形成的界面层具有明显的粘弹性, 其力学行为依赖于加载速率, 但无法通过有效的试验手段直接测取到界面层的关键性参数, 如界面强度及失效位移等。现有界面本构参数大多是基于文献及经验选取, 具有一定的主观性和随机性, 所以为了提高复合固体推进剂细观数值模型的准确性, 探寻一种有效的界面参数获取方法具有重要现实意义。本研究基于分子动力学方法生成能够反映HTPB/IPDI复合固体推进剂细观结构的颗粒填充模型, 并通过构建率相关内聚力模型, 结合试验与仿真曲线, 对界面参数进行反演分析。
2 细观模型为了实现从细观角度对HTPB/IPDI复合固体推进剂的仿真模拟, 须基于周期性假设, 建立起可反映推进剂细观真实构形的细观颗粒堆积模型。
2.1 颗粒填充模型目前对于颗粒填充体系结构的生成, 应用较为广泛的为分子动力学算法[13]、Monte-Carlo算法[14]等。综合算法效率、成熟度及后续有限元处理工作量等因素, 本文选用分子动力学算法来生成指定体积分数的HTPB/IPDI固体推进剂的颗粒填充模型, 具体配方见表 1。研究将基于二维颗粒填充模型来实现, 并视为平面应变问题对模型进行求解。
| 表 1 HTPB/IPDI复合推进剂典型配方 Tab.1 Typical formula of HTPB/IPDI composite propellant |
为了解HTPB/IPDI推进剂的基本细观形貌, 将推进剂试件在单轴载荷下拉断, 对断面进行显微观测, 结果见图 1。从图中可知, 断面中存在较多的尚无破损的大尺寸固体颗粒以及大颗粒脱离基体所留下的凹坑, 说明HTPB/IPDI推进剂在外界载荷作用时, 主要沿较大填充颗粒的表面开始脱粘破坏, 而小尺寸颗粒与基体混合均匀, 不见明显的脱粘现象, 这与文献[15]中对单一组分的HTPB/IPDI推进剂的电镜扫描结果较为一致。基于上述现实, 为提高推进剂细观有限元模型的计算效率及收敛性, 将铝粉颗粒视为溶入基体材料, 并基于多步法[16]计算其等效初始模量, 计算得到具体初始模量数值为0.732 MPa。
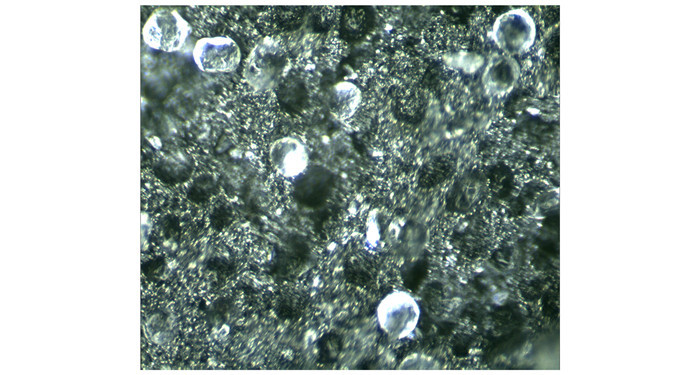
|
图 1 HTPB/IPDI复合固体推进剂断面显微图 Fig.1 Cross section micrograph of HTPB/IPDI composite solid propellant |
颗粒尺寸分布是建立HTPB/IPDI推进剂细观模型的关键信息, 文献[16]给出了与本文具有相同配方的HTPB复合固体推进剂基于微CT试验得到的细观颗粒尺寸分布情况, 见表 2。
| 表 2 HTPB/IPDI复合固体推进剂中颗粒尺寸分布 Tab.2 The dimension distribution of particles filled in HTPB/IPDI composite solid propellant |
根据表 1所给出的定制配方及表 2给出的颗粒尺寸分布信息, 基于分子动力学算法, 生成了颗粒填充系数为63.8%的HTPB/IPDI复合固体推进剂代表性体积单元模型, 模型及边界条件施加示意见图 2。
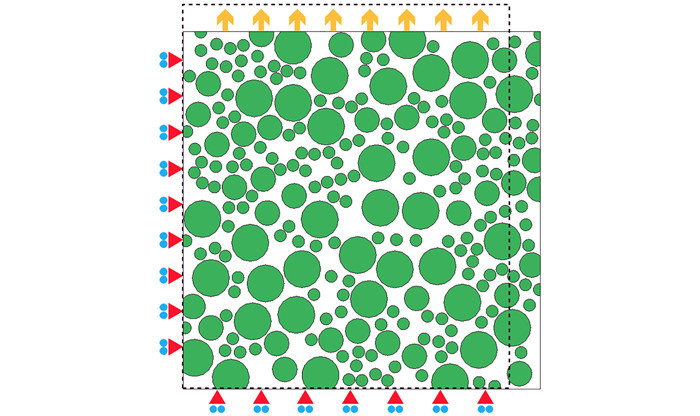
|
图 2 HTPB/IPDI复合固体推进剂细观填充模型及边界条件 Fig.2 The packing model of HTPB/IPDI composite solid propellant and boundary conditions |
实际HTPB/IPDI推进剂中, 以丁羟胶为粘合剂体系的粘接界面会表现出较为明显的粘弹特性, 所以需在传统的率无关内聚力模型的基础上引入粘性因素以表征界面所具有的粘弹属性。本文结合粘弹性标准机械模型与率无关内聚力本构关系来构建率相关界面牵引力-位移分离法则。
对于复合材料粘弹性力学行为研究中应用较为广泛的三参量固体模型, 即是由麦克斯韦模型与线性弹簧并联得到, 具有如下本构表述[12]:
| $ \eta \frac{{{\rm{d}}\sigma }}{{{\rm{d}}t}} + {E_2}\sigma = \eta \left( {{E_1} + {E_2}} \right)\frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} + {E_1}{E_2}\varepsilon $ | (1) |
式中,η为表征粘壶粘性的系数, 单位为MPa·s; E则为弹簧的弹性模量, 单位为MPa。
率无关内聚力模型采用指数型内聚力关系, 该模型定义界面法向牵引力Tn与张开位移间un存在如下关系[12]:
| $ \begin{array}{l} {{\bar T}_n} = - {{\bar \sigma }_{{\rm{max}}}}ze\frac{{{u_n}}}{{{\delta _{\rm{c}}}}}{\rm{exp}}\left( { - z\frac{{{u_n}}}{{{\delta _{\rm{c}}}}}} \right)\;\;\;\;\left( {{u_n} \le {\delta _{\rm{c}}}} \right)\\ {{\bar T}_n} = 0{\rm{ }}\;\;\left( {{u_n} \le {\delta _{\rm{c}}}} \right) \end{array} $ | (2) |
式中, e为自然常数, z=16e/9, 变量上方符号代表该变量为率无关模型中的参数;σmax为率无关界面强度, 即受载时细观界面所能达到的应力最大值, 单位为MPa;δc为临界位移, 为界面达到最大应力值时所对应的张开位移数值, 单位为mm, 界面张开位移大于临界位移后, 界面开始出现损伤, 界面应力进入软化下降阶段。
为了将率效应引入至内聚力模型中, 可将标准机械模型中的应力及应变分别以界面牵引力及界面位移替换, 而模型中的并联弹簧的弹性模量则以dTn/dun替换。对于三参量固体模型中麦克斯韦模型的弹簧弹性模量及粘壶粘性系数可分别以刚度系数k2(单位: MPa/mm)和内聚粘度ηCZ(单位: MPa·s/mm)替换。参量替换整理后, 可以得到率相关的内聚模型本构关系如下:
| $ {\eta ^{CZ}}\frac{{{\rm{d}}{T_n}}}{{{\rm{d}}t}} + {k_2}{T_n} = {\eta ^{{\rm{CZ}}}}\left[{\frac{{{\rm{d}}{{\bar T}_n}}}{{{\rm{d}}{u_n}}} + {k_2}} \right]\frac{{{\rm{d}}{u_n}}}{{{\rm{d}}t}} + {k_2}{\bar T_n} $ | (3) |
通过对模型中材料参数进行组合, 引入特征时间常数τ=ηCZ/k2(单位: s), 及参考分离速率dδ/dt=k2δc/ηCZ (单位: mm/s)。至此, 考虑率相关效应的内聚力模型构建完成。模型经过离散化, 表述为增量形式后(式4), 导入至Abaqus有限元平台中进行数值计算。
| $ {T_n}\left( t \right) = {\bar T_n}\left( t \right) + \frac{{{k_2}\left[{{u_n}\left( t \right)-{u_n}(t-\Delta t)} \right] + {T_n}(t - \Delta t) - {{\bar T}_n}(t - \Delta t)}}{{1 + {k_2}\frac{{\mathit{\Delta }t}}{{{\eta ^{{\rm{CZ}}}}}}}} $ | (4) |
从模型中可以看出, 率相关内聚力本构存在四个参数, 即两个率无关参数σmax和δc及两个率相关参数k2和ηCZ。文献[12]研究表明, 在较低水平的加载速率下, 率相关内聚力与率无关模型基本重合, 两个率相关参数k2和ηCZ对界面的分离法则影响较小, 因此可根据该规律, 结合低速率仿真及试验曲线首先反演得到两个率无关参数, 然后再基于中等速率下的试验曲线进行反演分析, 进而得到剩余的两个率相关参数。
3 参数获取 3.1 组分参数HTPB/IPDI组分参数主要为填充颗粒的弹性模量及泊松比以及基体固化胶片的松弛模量。颗粒参数依据文献[17]可知, AP:弹性模量为32447 MPa, 泊松比0.1433; Al:弹性模量68300 MPa, 泊松比0.33。
HTPB/IPDI固化胶片的松弛模量及其数学描述可通过应力松弛试验获取。应力松弛试验在QJ(倾技®, 上海)系列万能材料试验机上进行, 试件尺寸及装夹方式见图 3所示。
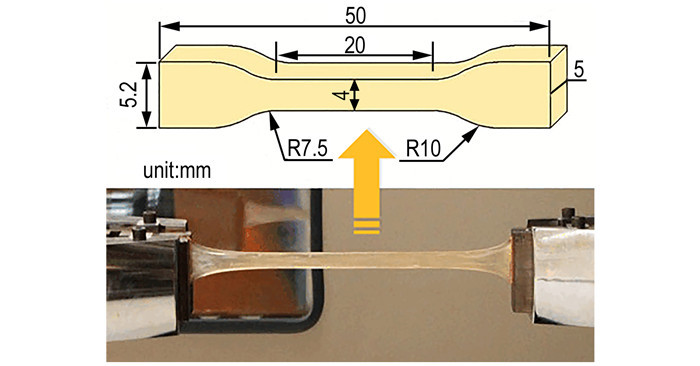
|
图 3 HTPB/IPDI固化胶片试件尺寸及装夹方式 Fig.3 The size and fixed type of test specimen of HTPB/IPDI curing film |
选定复合固体推进剂材料单轴力学试验中常用的中等应变率加载, 以0.03333/s将试件拉伸至100%应变后, 维持位移不变, 记录下随后600 s内试件力值随时间的变化情况, 单组试件进行5次试验, 最终结果取为5次试验均值。HTPB/IPDI固化胶片应力松弛试验结果曲线见图 4。对松弛试验曲线以Prony级数的形式进行拟合, 具体拟合表达式为[18]:
| $ E\left( t \right) = {E_\infty } + \sum\limits_{i = 1}^n {{E_i}{\rm{exp}}\left( { - \frac{t}{{{\tau _i}}}} \right)} $ | (5) |
式中, E∞为平衡模量, Ei和τi分别为第i个Maxwell单元的模量及松弛时间。拟合结果见图 4所示。由此得到了HTPB/IPDI固化胶片的粘弹性松弛行为描述, 进而可得基体胶片基于松弛模量的应力应变本构关系[19]:

|
图 4 HTPB/IPDI固化胶片应力-松弛曲线 Fig.4 Stress-relaxation curve of binder of HTPB/IPDI curing film |
| $ \sigma \left( t \right) = \int_0^t {\left( {{\mathit{E}_\infty } + \sum\limits_i^n {{E_i}{e^{ - \left( {t - \tau } \right)/{\tau _i}}}} } \right)} \dot \varepsilon \left( \tau \right){\rm{d}}\tau $ | (6) |
目前尚无有效的试验手段直接测取细观界面参数, 故本研究采用反演分析技术来获取最终界面参数数值。
反演算法主要涉及到三个主体部分: Hooke-Jeeves算法[20]程序、有限元调用及目标函数构建。Hooke-Jeeves算法模块为反演分析主程序, 其通过不断调整对象参数, 并调用有限元软件进行计算, 然后依据计算结果与试验数值进行对比, 计算出目标函数数值, 如此循环, 从而实现最终的优化目标。有限元软件调用模块则是基于已导入的有限元数值模型, 代入Hooke-Jeeves算法模块传递而来的对应参数值, 建立新的分析作业, 并计算完成对应参数下的模型计算。目标函数构建在于建立起能够反映仿真数值与试验数值偏差的目标函数, 其形式如下:
| $ {\rm{min}}R = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left[{E\left( {{x_i}} \right)-S\left( {{x_i}} \right)} \right]}^2}\;\;\;} i = 1, 2, 3 \ldots, n $ | (7) |
式中,E(xi)及S(xi)分别为离散的试验曲线数据点及仿真结果数据点。算法具体实现流程如图 5所示。
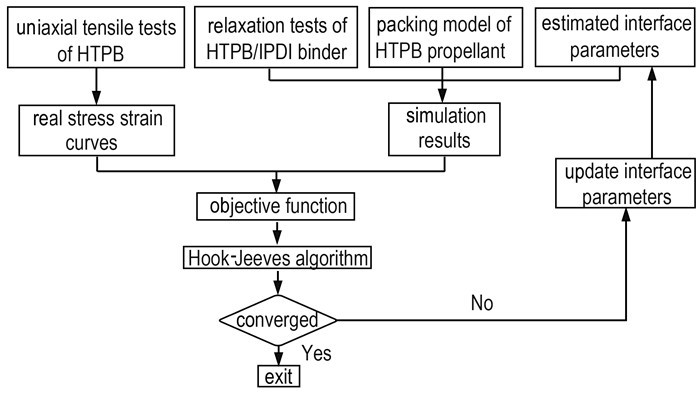
|
图 5 HTPB/IPDI推进剂界面参数反演流程图 Fig.5 Flow chart of interface parameters inversion process of HTPB/IPDI propellant |
由于反演算法需依赖于实际试验曲线而实现, 因此需对HTPB/IPDI进行宏观单轴拉伸试验。试验平台与前节松弛试验平台, 保持一致, 试件由同一批浇筑坯料按航天部标准QJ924-85[21]切割为哑铃状后通过配套夹具固定于试验平台之上。
结合2.2节末所述的参数获取路线, 单轴拉伸试验采用3组拉伸速率(0.1,5,20 mm·min-1)加载。其中0.1 mm·min-1用于率无关参数获取, 而5 mm·min-1和20 mm·min-1试验用于反演得到率相关参数。单个速率保证5个有效数据的获取, 结果取为5次试验均值, 试验结果见图 6。从图中可以看出, HTPB/IPDI推进剂力学行为具有明显的应变率相关性, 加载速率越高, 材料初始模量及应力幅值越大。
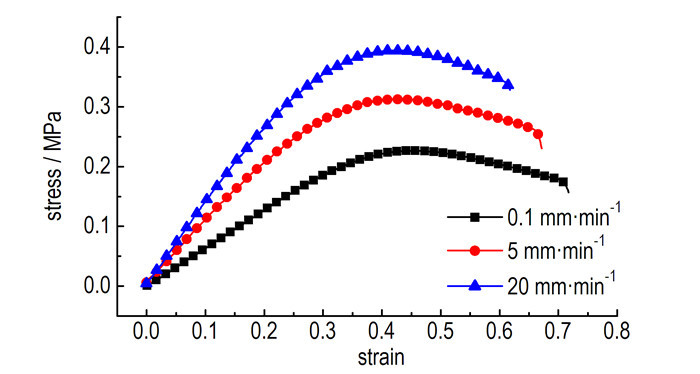
|
图 6 不同拉伸速率下HTPB/IPDI推进剂应力-应变曲线 Fig.6 The stress-strain curves of HTPB/IPDI propellant at different strain rates |
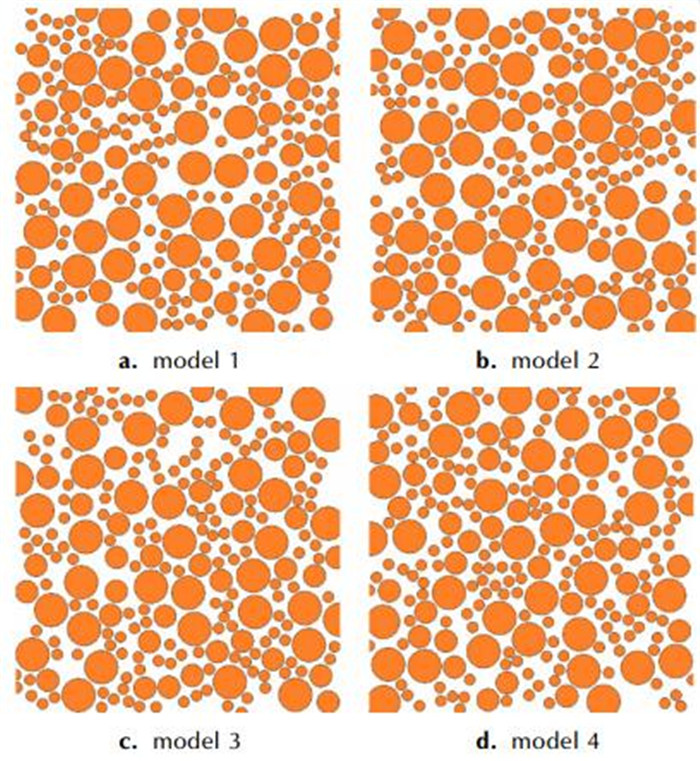
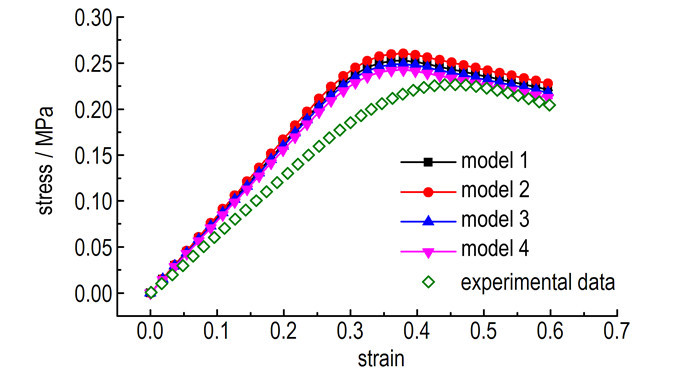
依据表 1所给定的配方, 对HTPB/IPDI复合固体推进剂进行4次建模, 得到包含不同颗粒随机分布信息的推进剂细观模型, 如图 7所示, 可以看出, 四次建模得到的细观模型中, 填充颗粒的分布位置不一, 体现了HTPB/IPDI推进剂的细观结构随机性。代入3.1节得到的组分参数, 界面参数依据文献[7-8]给出的参数作为初始值, 对细观模型施加轴向位移载荷, 计算该过程中推进剂的细观响应, 结果如图 8所示。由图 8可以看出不同随机模型的计算结果基本一致, 不存在明显差异, 可以认为在保证颗粒体积分数及粒径平均尺寸不变的前提下, 颗粒的随机性分布不会影响复合固体推进剂的力学性能。图 8中同时给出了对应载荷下HTPB推进剂的宏观试验曲线, 由散点形式表出, 可以看出, 基于初始界面参数得到的仿真曲线与实际试验结果存在较大的差距, 须对界面参数进行反演优化。
|
图 7 具有不同颗粒随机分布性HTPB/IPDI复合固体推进剂细观填充模型 Fig.7 Random packing models of HTPB/IPDI composite solid propellant with different spatial distribution of particles |
|
图 8 不同颗粒随机分布性HTPB/IPDI复合固体推进剂细观数值计算结果 Fig.8 Finite element computing results of HTPB/IPDI composite solid propellant with different spatial distribution of particles |
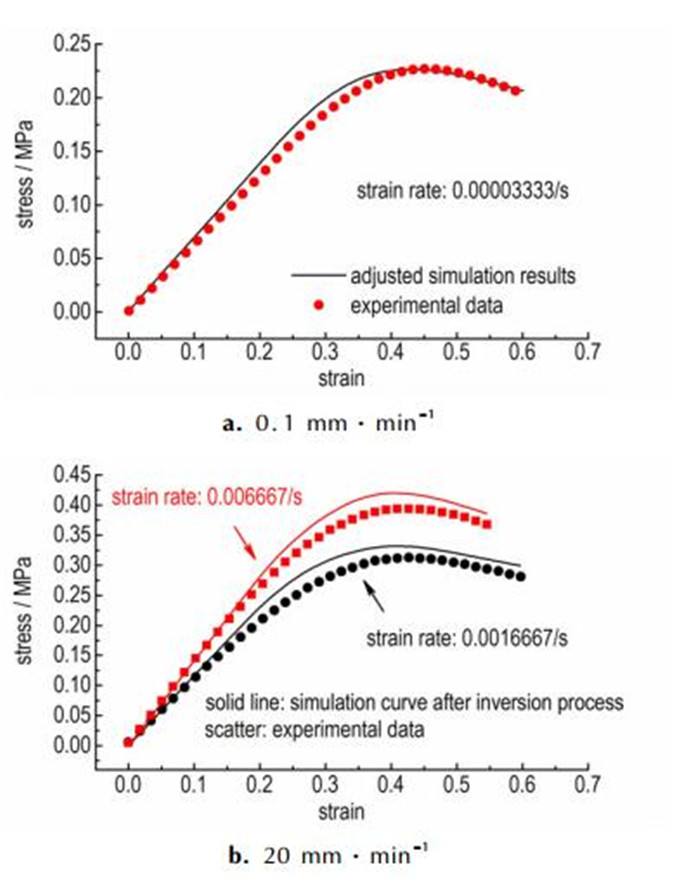
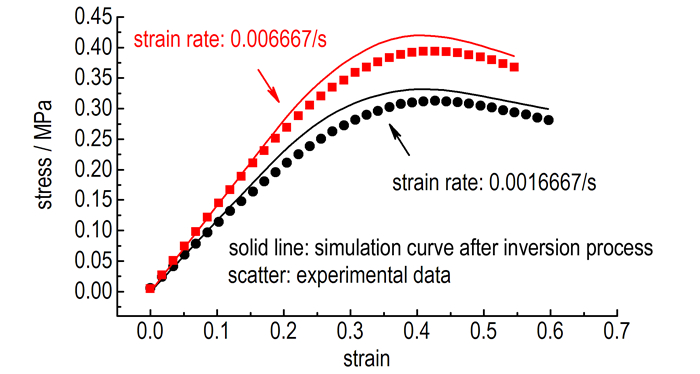
结合2.2节所述的界面参数获取方式及3.2节中宏观单轴拉伸曲线及反演流程, 通过有限元计算及反演分析, 仿真结果见图 9及图 10, 反演优化后的界面参数见表 3。图 9为细观仿真损伤形貌图与真实推

|
图 9 HTPB/IPDI固体推进剂细观模型仿真脱湿形貌和宏观拉伸脱湿形貌显微图 Fig.9 Computed debonding morphology and micrograph of particle dewetting of HTPB/IPDI solid propellant in meso level and micro level |
|
图 10 试验结果与反演仿真结果对比 Fig.10 Comparison of the experimental results and inverted simulation ones |
| 表 3 率相关内聚模型参数 Tab.3 Parameters of rate-dependent cohesive zone model |
进剂受载过程中的表面的显微图的对比, 从图 9中可以看出, 所建细观模型能够较好地反映出HTPB/IPDI的细观脱湿特性。图 10为反演优化后的细观模型仿真曲线与宏观试验曲线对比。可以看出, 经过反演分析, 仿真曲线与实际试验曲线吻合度较高, 但同时也存在一定差距。对于差距产生的原因, 主要源自如下几点:
(1) 建立的HTPB/IPDI复合固体推进剂的数值模型为二维层面, 与实际材料的三维结构应力状态存在一定异同, 现阶段三维模型的建立及计算存在诸多问题, 而二维简化模型能够在一定程度上较好的反映出固体推进剂的宏观力学行为, 所以目前针对固体推进剂的细观数值研究均是在二维层面上进行。
(2) 建立的细观模型中, 初始无载阶段颗粒与基体间均粘接完好, 而实际固体推进剂在制造中会因生产工艺导致推进剂存在颗粒破碎, 空穴及粘结剂包裹不全等初始缺陷, 从而导致实际推进剂的初始刚度要比不含缺陷完美粘接的推进剂低。
(3) 所建立推进剂细观模型中, 填充颗粒均为圆形颗粒, 而在实际固体推进剂的构成中, 除球形颗粒外, 还存在一些异状颗粒, 异状颗粒相对于规则形状的颗粒更容易发生脱粘现象, 故而导致推进剂的力学性能出现一定程度的劣化。
总体而言, 本研究结合颗粒填充模型、率相关内聚力模型以及反演优化算法构建的颗粒填充细观模型可以有效地体现出HTPB/IPDI复合固体推进剂的宏观力学性能, 能够用于描述及预测该推进剂的宏观力学行为。
4.3 模型验证可通过所建模型及参数对其他加载速率下的复合固体推进剂的宏观应力应变行为进行预测, 并将预测结果与实际试验结果进行对比来验证模型及参数的准确性。验证试验选用50, 100 mm·min-1加载速率, 数值计算预测与实际试验曲线之间的对比如图 11所示。图 11中信息表明, 预测曲线与试验结果吻合较好, 基本特征及走势较为一致, 说明所建立的细观数值模型及率相关内聚力本构关系可以有效反映出实际复合固体推进剂中颗粒与基体间界面的粘接情况及其宏观力学行为。
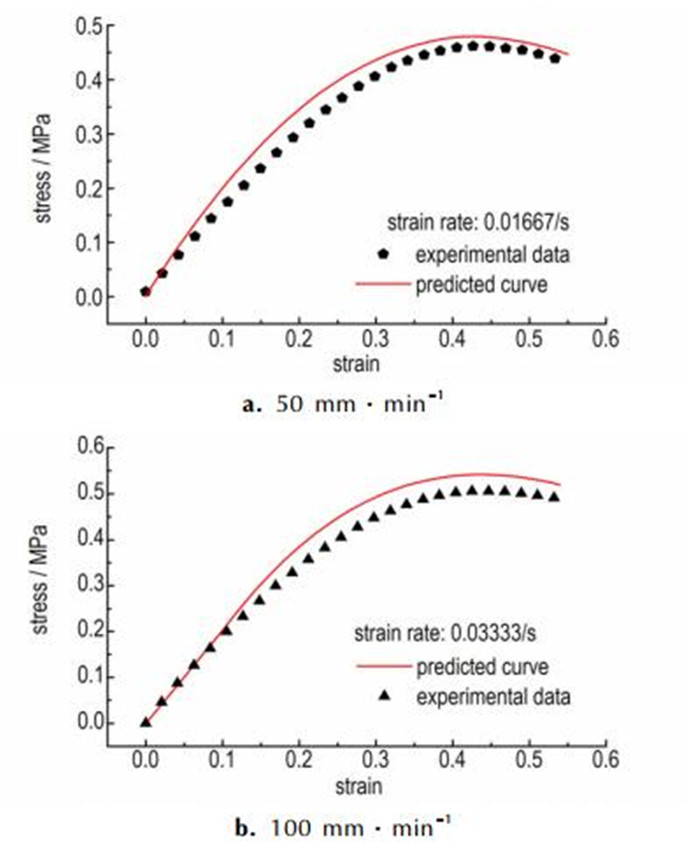
|
图 11 内聚力模型率相关参数验证 Fig.11 Verification of the rate-dependent parameters of cohesive zone model |
(1) 基于分子动力学算法及具有内聚力本构关系的粘接单元所建立的HTPB/IPDI推进剂细观模型能够有效反映出固体推进剂的细观特征及受载过程中的细观结构变化情况。
(2) 在传统内聚力模型的基础上, 引入粘弹性因素, 构建出可以考虑率效应的内聚力模型, 扩展了内聚力模型对于HTPB/IPDI推进剂此类粘弹性材料的适用性。
(3) 采用颗粒填充模型及参数反演优化后的率相关内聚力本构关系所构建的HTPB/IPDI推进剂细观仿真模型, 对50及100 mm·min-1下的推进剂宏观粘弹响应进行了验证, 结果表明模型可有效体现出HTPB/IPDI固体推进剂的力学性能的应变率相关性。可在3.33×10-5/s~0.03333/s应变率范围内, 对HTPB/IPDI固体推进剂的宏观应力应变关系进行有效预测。
(4) 细观数值模型的建立尚存在一定不足, 主要为HTPB/IPDI基体胶片与全配方推进剂中基体材质的粘弹性因固化反应的微观环境有别而存在一定差异, 后续研究将针对该问题, 在基体胶片制备上做出进一步的探索和改进。
| [1] |
许进升. 复合推进剂热粘弹性本构模型实验及数值仿真研究[D]. 南京: 南京理工大学, 2013.
XU Jin-sheng. Research on thermos-viscoelastic constitutive model and numerical simulation method of composite propellant[D]. Nanjing: Nanjing University of Science and Technology, 2013. |
| [2] |
常武军. 复合固体推进剂细观损伤及其数值仿真研究[D]. 南京: 南京理工大学, 2013.
CHANG Wu-jun. Research on microstructural damage and its numerical simulation method for composite solid propellant[D]. Nanjing: Nanjing University of Science and Technology, 2013. |
| [3] |
张兴高, 张炜, 芦伟, 等. HTPB推进剂填料/基体界面粘结性能老化特性研究[J].
含能材料, 2009, 17(3): 269-273. ZHANG Xing-gao, ZHANG Wei, LU Wei, et al. Aging characteristics of interfacial adhesive property of filler/binder matrix for HTPB propellant[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2009, 17(3): 269-273. |
| [4] |
李高春, 刘著卿, 张璇, 等. SEM与数字图像法分析复合推进剂细观破坏[J].
含能材料, 2013, 21(3): 330-333. LI Gao-chun, LIU Zhu-qing, ZHANG Xuan, et al. Mesoscale failure in solid propellant by coupling SEM and digital image correlation method[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2013, 21(3): 330-333. |
| [5] |
Mortazavi B, Baniassadi M, Bardon J, et al. Modeling of two-phase random composite materials by finite element, Mori-Tanaka and strong contrast methods[J].
Composites Part B: Engineering, 2013, 45(1): 1117-1125. DOI:10.1016/j.compositesb.2012.05.015 |
| [6] |
Matouš K, Inglis H M, Gu X F, et al. Multiscale damage modeling of solid propellants: theory and computational framework[R]. AIAA 2005-4347: 2005.
|
| [7] |
Chang W J, Ju Y T, Han B. Numerical simulation of particle/matrix interface failure in composite propellant[J].
Journal of China Ordnance, 2012, 8(3): 146-153. |
| [8] |
曲凯, 张旭东, 李高春. 复合固体推进剂非线性界面脱粘的力学性能研究[J].
弹箭与制导学报, 2010, 30(3): 114-118. QU Kai, ZHANG Xu-dong, LI Gao-chun. Research on mechanics performance of composite propellant with nonlinear interface debonding[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(3): 114-118. |
| [9] |
职世君, 孙冰, 张建伟. 基于表面粘结损伤的复合固体推进剂细观损伤数值模拟[J].
推进技术, 2013, 34(2): 273-279. ZHI Shi-jun, SUN Bing, ZHANG Jian-wei. Numerical simulation of solid propellant mesoscopic damage using surface-based cohesive approach[J]. Journal of Propulsion Technology, 2013, 34(2): 273-279. |
| [10] |
Kulkarni M G, Geubelle P H, Matouš K. Multi-scale modeling of heterogeneous adhesives: Effect of particle decohesion[J].
Mechanics of Materials, 2009, 41(5): 573-583. DOI:10.1016/j.mechmat.2008.10.012 |
| [11] |
Han B, Ju Y, Zhou C. Simulation of crack propagation in HTPB propellant using cohesive zone model[J].
Engineering Failure Analysis, 2012, 26(12): 304-317. |
| [12] |
韦震. 推进剂细观粘接界面力学模型及参数获取方法研究[D]. 南京: 南京理工大学, 2014.
WEI Zhen. Research on the model and parameters acquisition of the meso interface properties of composite propellant[D]. Nanjing: Nanjing University of Science and Technology, 2014. |
| [13] |
Kochevers S. Random sphere packing model of heterogeneous propellants[D]. Champaign: University of Illinois at Urbana-Champaign, 2002.
|
| [14] |
王星, 王玉璋. 颗粒填充型复合材料有效导热系数的数值计算方法[J].
材料导报, 2013, 27(10): 143-147. WANG Xing, WANG Yu-zhang. Numerical calculation method for effective thermal conductivity of particle filled composites[J]. Materials Review, 2013, 27: 143-147. DOI:10.3969/j.issn.1005-023X.2013.10.036 |
| [15] |
宋丹平. 固体推进剂细观力学与本构关系研究[D]. 武汉: 武汉理工大学, 2008.
SONG Dan-ping. Research on the mesomechanics and constitutive model of propellant[D]. Wuhan: Wuhan University of Technology, 2008. |
| [16] |
马昌兵. 复合固体推进剂细观结构建模及其力学行为数值模拟[D]. 西安: 第二炮兵工程学院, 2011.
MA Chang-bing. Research on mesostructure modeling and mechanical behaviors numerical simulation of composite solid propellant[D]. Xi'an: The Second Artillery Engineering University, 2011. |
| [17] |
Matouš K, Geubelle P H. Finite element formulation for modeling particle debonding in reinforced elastomers subjictde to finite deformations[J].
Computer Methods in Applied Mechanics and Engineering, 2006, 196: 620-633. DOI:10.1016/j.cma.2006.06.008 |
| [18] |
许进升, 鞠玉涛, 郑健, 等. 复合固体推进剂松弛模量的获取方法[J].
火炸药学报, 2011, 34(5): 58-62. XU Jin-Sheng, JU Yu-Tao, ZHENG Jian, et al. Acquisition of the relaxation modulus of composite solid propellant[J]. Chinese Journal of Explosives & Propellants,, 2011, 34(5): 58-62. |
| [19] |
Jung G D, Youn S K. A nonlinear viscoelastic constitutive model of solid propellant[J].
International Journal of Solids & Structures, 1999, 36(25): 3755-3777. |
| [20] |
Hooke R, Jeeves T A. "Direct Search" solution of numerical and statistical problems[J].
Journal of the ACM, 1961, 8(2): 212-229. |
| [21] |
QJ924-85, 复合固体推进剂单向拉伸试验方法[S]. 北京: 中华人民共和国航天工业部标准.
|
The mesoscale simulation model of HTPB/IPDI propellant was developed based on event-driven molecular dynamics method and rate-dependent cohesive zone method. The model is cable of describing the rate-dependent mechanical behavior of HTPB/IPDI propellant.




