端羟基聚丁二烯(HTPB)复合固体推进剂是固体火箭发动机的动力之源, 作为一种以聚合物丁羟粘合剂为基体的高填充颗粒复合材料, 其物理化学性能弱于金属壳体、绝热层及包覆层。在贮存期间的载荷/环境谱的作用下, 其力学性能会随着贮存时间的增加而不断降低[1-2]。因而为了保证火箭发动机的正常使用, 需要对HTPB推进剂的贮存寿命进行预估。目前, 国内外常用的方法是将高温加速寿命试验和Arrhenius方程相结合, 建立推进剂力学性能随贮存时间变化的老化模型, 进而外推常温贮存下的使用寿命[3]。但Arrhenius方程将活化能假设为与温度无关的常数, 这给推进剂的寿命预估引入误差[4], 杨根等[5]通过选择最大延伸率随贮存时间的变化关系为幂函数模型、周洁等[6]对Arrhenius方程中的温度参数进行了分段, 有效地对误差进行了修正。为了使高温加速寿命试验结果和实际贮存状况相吻合, 王斌等[7]结合Arrhenius方程和Miner准则, 推导出了推进剂贮存使用寿命的累积损伤—反应论模型, 解决了变化环境下推进剂的寿命预估问题。在对模型参数的求解上, 洪东跑等[8]提出了一种广义线性模型, 有效改善了推进剂贮存寿命与可靠性评估的精度。推进剂在贮存过程中的性能变化比较复杂, 在老化的不同阶段呈现出不同的特点, 常用的老化模型很难对推进剂不同老化阶段的特点进行准确地描述, 分段老化模型的相关研究还未见报道。
为了对老化不同阶段的特点进行准确描述, 本研究通过高温加速寿命试验中HTPB推进剂最大延伸率随贮存时间的变化关系, 建立了推进剂最大延伸率随贮存时间变化的分段老化模型, 运用时温等效原理, 结合高温加速老化和常温贮存的时间转化关系, 对HTPB推进剂在常温(25 ℃)条件下的贮存寿命进行了预估。为了验证该分段老化模型的准确性, 对指数模型、对数模型、幂函数模型和分段老化模型的相关系数和标准差进行了对比分析。
2 试验 2.1 试件的老化及测试本研究选取某型号哑铃型HTPB推进剂试件进行试验, 试件的高温加速老化参照GJB 770B-2005方法506.1进行。试件用铝塑袋密封, 放入DU288型电热油浴恒温箱进行一年的加速寿命试验, 老化温度分别为(50±1) ℃、(60±1) ℃、(70±1) ℃, 相对湿度小于50%RH。每一个月取出定量的试件(保证每个测试点的老化试件不少于五组), 在密闭的干燥器中自然冷却24 h, 然后使用Instron 5982型材料拉伸机, 按照GJB770B-2005中方法413.1对试件进行最大延伸率测试, 并记录试验数据, 绘制HTPB推进剂最大延伸率随贮存时间的变化曲线[9]。采用洛马诺夫斯基准则(t检验准则)剔除异常数据, 选用正常试验数据进行分析。
2.2 试验结果及分析HTPB推进剂老化过程中伴随着后固化、氧化交联和降解断链的相互作用, 另外还存在脱湿、裂纹、空穴的增加和生长等过程[10-11]。试样最大延伸率随贮存时间的变化曲线如图 1所示。图 1显示, 三个老化温度下, 其最大延伸率随贮存时间的变化趋势相同, 说明三个温度下推进剂遵循相同的老化机理。另外, 随着温度升高, 推进剂延伸率的反应速率明显增加, 这是因为高温条件下加速了推进剂的老化反应进程。总体而言, HTPB推进剂最大延伸率随贮存时间的增加呈下降趋势, 但是在反应速率上, 先快速下降, 然后速率变缓, 最后反应速率趋于零, 因此宏观上将HTPB推进剂的老化分成了三个不同的反应阶段[10-12]。
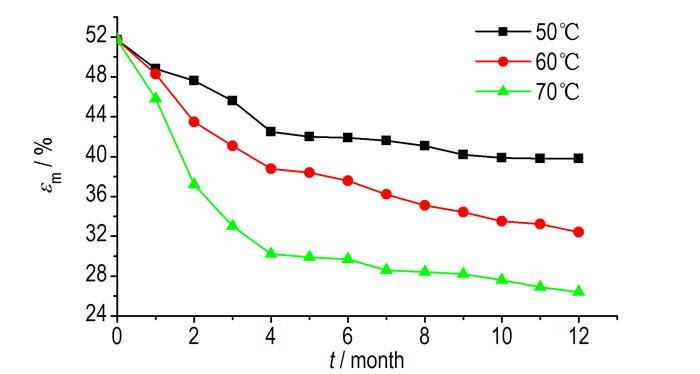
|
图 1 HTPB推进剂最大延伸率随贮存时间变化曲线 Fig.1 The change curves of the maximum elongation of HTPB propellant with storage time |
(1) 老化初期(0~4月):最大延伸率呈快速下降趋势。这一阶段存在后固化和氧化交联作用, 同时推进剂的脱湿现象明显, 导致推进剂最大延伸率的快速降低。;
(2) 老化中期(4~6月):最大延伸率的变化呈现出一个平衡区。这个时期推进剂的后固化作用已经完全, 而氧化交联和降解断链的反应在这一阶段几乎处于平衡的状态, 推进剂内部的空穴不断增加、生长、融合, 总体上表现为老化反应速率的缓慢降低;
(3) 老化末期(6月之后):最大延伸率继续降低, 但是反应速率逐渐趋于零。这一阶段推进剂氧化交联的作用略大于降解断链, 同时推进剂的内部裂纹逐渐增长, 直到推进剂发生断裂, 最大延伸率的变化速率在整体上呈现出先缓慢下降后趋于零的趋势。
本试验得出的推进剂最大延伸率变化趋势以及老化分段与文献[12]的结论一致, 关于老化机理的相关试验, 文献[12]中有详细的论述, 本文不再赘述。
3 数据处理及分析 3.1 三种老化模型的相关性分析目前, 国内外常用指数模型、对数模型和幂函数模型[13]对HTPB推进剂高温加速寿命试验数据进行分析, 进而对常温贮存下推进剂的使用寿命进行预估。
指数模型:
| $ {\varepsilon _{\rm{m}}} = {\varepsilon _{{\rm{m0}}}}{{\rm{e}}^{-kt}} $ | (1) |
对数模型:
| $ {\varepsilon _{\rm{m}}} = {\varepsilon _{{\rm{m0}}}}{\rm{ + }}k\lg t $ | (2) |
幂函数模型:
| $ {\varepsilon _{\rm{m}}} = {\varepsilon _{{\rm{m0}}}}{\rm{ + }}k{t^\alpha }, \;\;\left( {a = 0.1, 0.2, \ldots, 0.9, 10} \right) $ | (3) |
式中, εm为HTPB的最大延伸率,%; k为老化反应速率常数; t为老化反应时间; εm0、α为常数。其中α=1.0时, 幂函数模型直接转化为线性模型, 即:
| $ {\varepsilon _{\rm{m}}} = {\varepsilon _{{\rm{m0}}}}{\rm{ + }}kt $ | (4) |
根据高温加速寿命试验的结果, 借助最小二乘法对三种老化模型的参数进行回归求解, 并对三种老化模型作相关性分析。根据三个老化温度下的计算结果得出, 幂函数模型在α=0.2时回归效果最好。参数拟合及相关性分析结果如表 1所示, 其中, R为相关性系数, R0.01为显著性水平为0.01时的临界相关系数。
| 表 1 参数拟合及相关性分析 Tab.1 Parameter fitting and correlation analysis |
根据表 1中的分析结果可以得出, 三种老化模型在60 ℃条件下的拟合结果相关性最好, 因而选取60 ℃条件下的老化试验数据, 对三种老化模型进行分段相关性分析。分析结果如表 2所示。
| 表 2 分段相关性分析 Tab.2 Segmented correlation analysis |
从表 1和表 2的分析结果可以看出, 单一老化模型与老化试验数据的整体相关性和分段相关性存在区别, 整体相关性高的模型在老化过程的某一个分段可能相关性较低, 同样整体相关性较低的模型在某一老化分段可能有较高的相关性。在老化初期(0~4月), 对数模型的相关性最好; 在老化中期(4~6月), 指数模型的相关性大于另外两种老化模型; 老化末期(6月之后), 幂函数模型的相关性最优。为了提高老化模型的准确性, 可以考虑对老化过程进行分段建模。
3.2 温度对老化反应速率的影响高温加速老化方法假设固体推进剂的老化反应速率常数k服从Arrhenius方程[14-15]:
| $ k = A{{\rm{e}}^{-{E_{\rm{a}}}/RT}} $ | (5) |
式中, Ea为表观活化能,J·mol-1; R为普适气体常数,8.314 J·mol-1·K-1; T为绝对温度,K; A为常数。
根据表 1中老化反应速率随老化温度的变化关系, 对式(5)进行回归分析, 拟合得到参数Ea、A的值, 并外推得到常温25 ℃条件下HTPB推进剂的老化反应速率常数k25 ℃。参数回归结果如表 3所示。
| 表 3 参数回归及老化反应速率常数外推结果 Tab.3 The results of parameter regression and extrapolation of aging reaction rate constant |
根据表 1的分析结果可知, 60 ℃条件下老化模型与试验数据的拟合情况最好, 根据粘弹性材料的时温等效原理[16-17], 以该温度条件下老化反应一个月的试验数据为基准, 外推出常温25 ℃条件贮存时的等效转换时间。转换结果如表 4中所示。
| 表 4 等效时间转换结果 Tab.4 The results of equivalent time conversion |
通过第2部分的分析可以得出, 三种不同的老化模型在老化过程的不同阶段, 其相关程度存在差别, 可以根据分段相关性最优的老化模型特点, 对HTPB推进剂的贮存老化建立分段模型。即:
| $ {\varepsilon _{\rm{m}}} = \left\{ \begin{array}{l} {\varepsilon _{{\rm{m0}}}}{\rm{ + }}{k_1}\lg {t_1}, 1 \le {t_1} \le 4\\ {\varepsilon _{{\rm{m1}}}}{{\rm{e}}^{-{k_2}{t_2}}}, \;\;\;\;\;0 \le {t_2} \le 3\\ {\varepsilon _{{\rm{m2}}}}{\rm{ + }}{k_3}t_3^\alpha, \;\;\;\;{t_3} \ge 0 \end{array} \right. $ | (6) |
式中, εm1和εm2分别为老化4个月和6个月后推进剂的最大延伸率。
根据某温度下高温加速寿命试验数据, 结合时温等效原理, 以最大延伸率下降至30%为失效判据[18], 就可以外推得到常温25 ℃条件下HTPB推进剂的贮存寿命。以60 ℃加速寿命试验结果为例, 将数据分析结果代入式(6), 可得分段老化模型为:
| $ {\varepsilon _{\rm{m}}} = \left\{ {\begin{array}{*{20}{l}} {51.7 - 14.3436{\rm{lg}}{t_1},\;\;\;\;\;\;\;1 \le {t_1} \le 4}\\ {43.0643{{\rm{e}}^{ - 0.0358{t_2}}},\;\;\;\;\;\;\;\;\;\;\;\;0 \le {t_2} \le 3}\\ {40.0887 - 12.5516t_3^{0.2},\;\;\;\;{t_3} \ge 0} \end{array}} \right. $ | (7) |
由式(7)可以看出, 在老化中期结束时, HTPB推进剂最大延伸率仍旧满足使用要求, 推进剂的失效变质发生在老化末期。根据时温等效原理, 代入常温25 ℃的老化反应速率常数k25 ℃, 外推出该型号HTPB推进剂在常温贮存时的使用寿命为139.2523月, 即11.60年, 该分段老化模型预估得到的推进剂贮存寿命和常温外推试验结果12.8年相比, 相对误差为9.37%, 且低于常温外推试验结果, 从安全性的角度上考虑满足实际使用需求。
假设建立的分段老化模型和HTPB推进剂的贮存状况能够有效吻合, 则该模型对应的回归结果的相关系数和标准偏差要优于另外三种模型, 寿命预估结果和常温外推试验结果的相对误差也要低于另外三种老化模型。为了验证假设的正确性, 将分段老化模型和指数模型、对数模型以及幂函数模型的相关系数最大值Rmax、最小值Rmin、标准差Rstd以及寿命预估结果进行对比分析。结果如表 5所示。
| 表 5 四种模型的对比分析结果 Tab.5 Comparative analysis results of four models |
由表 5中四种模型的相关性分析结果可以看出, 三种常用的老化模型中, 对数模型的相关性最好, 但是相关系数的标准差较高, 模型的稳定性和指数模型、幂函数模型相比较差, 不利于得出准确的推进剂老化预估寿命。而分段老化模型的相关系数R>0.95, 与对数模型的相关性基本相同, 同时标准差Rstd < 0.015, 回归结果要优于对数模型, 即分段老化模型可以在较高的稳定性水平上保证模型与老化结果的相关性。从寿命预估的对比分析结果可以得出, 分段老化模型、指数模型和对数模型对推进剂的寿命预估结果均低于常温外推试验结果, 但是分段老化模型的相对误差要优于指数模型和对数模型。幂函数模型的寿命预估结果大于常温外推结果, 从安全性上考虑不满足实际使用需求。综合相关系数最大值、最小值、标准差以及寿命预估结果, 分段老化模型可以准确可靠地对HTPB推进剂的贮存寿命进行预估。
5 结论(1) 根据HTPB推进剂在50, 60, 70 ℃三个温度下的高温加速寿命试验, 将推进剂的老化机理按照最大延伸率快速下降、平衡变化和缓慢降低过程分成三个阶段进行分析, 并结合三个阶段的老化反应特点以及指数模型、对数模型和幂函数模型的分段相关性分析, 建立了推进剂贮存老化的分段模型;
(2) 根据时温等效原理, 结合高温加速寿命试验结果, 运用分段老化模型预估某型号HTPB推进剂在常温25 ℃条件下的贮存寿命为11.60年。和常温外推试验结果12.8年相比, 相对误差为9.37%, 且低于常温外推试验结果, 从安全性的角度上考虑满足实际使用需求。与指数模型、对数模型以及幂函数模型相比, 该模型的相关系数R>0.95, 标准差Rstd < 0.015, 回归结果最优, 该模型可以作为参考运用于HTPB推进剂贮存寿命预估的研究中。
| [1] |
侯林法.
复合固体推进剂[M]. 北京: 中国宇航出版社, 1994: 371-375.
HOU Lin-fa. Composite solid propellant[M]. Beijing: China Aerospace Publishing House, 1994: 371-375. |
| [2] |
庞爱民.
固体火箭推进剂理论与工程[M]. 北京: 中国宇航出版社, 2014: 129-139.
PANG Ai-min. Theory and engineering of solid rocket propellant[M]. Beijing: China Aerospace Publishing House, 2014: 129-139. |
| [3] |
Huang W, Duane L. An alternative degradation reliability modeling approach using maximum likelihood estimation[J].
IEEE Transactions on Reliability, 2005, 54(2): 310-317. |
| [4] |
高大元, 何碧, 何松伟, 等. Arrhenius方法的局限性讨论[J].
含能材料, 2006, 14(2): 132-135. GAO Da-yuan, HE Bi, HE Song-wei, et al. Discussion on limitation of the Arrhenius methodology[J]. Chinese Journal of Energetic Materials, 2006, 14(2): 132-135. |
| [5] |
杨根, 赵永俊, 张炜, 等. HTPB推进剂贮存期预估模型研究[J].
固体火箭技术, 2006, 29(4): 283-285. YANG Gen, ZHAO Yong-jun, ZHANG Wei, et al. Investigation on prediction model for storage life of HTPB propellants[J]. Journal of Solid Rocket Technology, 2006, 29(4): 283-285. |
| [6] |
周洁, 姚军, 宋燕. 基于分段非线性Arrhenius的贮存寿命评估方法[J].
北京航空航天大学学报, 2015, 41(4): 744-750. ZHOU Jie, YAO Jun, SONG Yan. Storage life evaluation method based on segmented nonlinear Arrhenius model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 744-750. |
| [7] |
王斌, 常新龙. 固体火箭推进剂贮存使用寿命的累积损伤—反应论模型[J].
弹箭与制导学报, 2007, 27(1): 171-173. WANG Bin, CHANG Xin-long. The cumulative damage-reaction theory life model to the storage and usage of solid rocket propellant[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(1): 171-173. |
| [8] |
洪东跑, 王英华, 管飞, 等. 基于广义线性模型的固体推进剂贮存寿命评估[J].
北京航空航天大学学报, 2015, 41(4): 29-32. HONG Dong-pao, WANG Ying-hua, GUAN Fei, et al. Storage life assessment for solid propellant based on generalized linear model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 29-32. |
| [9] |
GJB 770B-2005[S], 火药试验方法: 200-204, 262-266.
GJB 770B-2005[S], Test method of propellant: 200-204, 262-266. |
| [10] |
Christiansen A G, Layton L H, Carpenter R L. HTPB propellant aging[J].
J Spacecraft, 1981, 18(3): 211-215. DOI:10.2514/3.57807 |
| [11] |
沈庭芳, 赵伯华. 固体推进剂空穴损伤的理论与试验研究[J].
推进技术, 2002, 23(1): 71-73. SHEN Ting-fang, ZHAO Bo-hua. Analyses of theory and experiment for void damage of solid propellant[J]. Journal of Propulsion Technology, 2002, 23(1): 71-73. |
| [12] |
张兴高. HTPB推进剂贮存老化特性及寿命预估研究[D]. 长沙: 国防科学技术大学, 2009.
ZHANG Xing-gao. Study on the aging properties and storage life prediction of HTPB propellant[D]. Changsha: National University of Defense Technology, 2009. |
| [13] |
唐国金, 申志彬, 田四朋, 等. 固体火箭发动机药柱概率贮存寿命预估[J].
兵工学报, 2012, 33(3): 301-306. TANG Guo-jin, SHEN Zhi-bin, TIAN Si-peng, et al. Probabilistic storage life prediction of solid rocket motor grain[J]. Acta Armamentarii, 2012, 33(3): 301-306. |
| [14] |
王国强, 史爱娟, 丁黎, 等. 丁羟推进剂的热加速老化力学性能及寿命预估[J].
火炸药学报, 2015, 38(1): 47-50. WANG Guo-qiang, SHI Ai-juan, DING Li, et al. Mechanical properties of HTPB propellant after thermal accelerated aging and its life prediction[J]. Chinese Journal of Explosives & Propellants, 2015, 38(1): 47-50. |
| [15] |
傅惠民, 杨立保, 林逢春, 等. 固体推进剂贮存寿命整体预测方法[J].
机械强度, 2007, 29(5): 754-759. FU Hui-min, YANG Li-bao, LIN Feng-chun, et al. Integral method for storage life prediction of solid propellant[J]. Journal of Mechanical Strength, 2007, 29(5): 754-759. |
| [16] |
邹思斯, 严聪, 马岑睿, 等. 定应变下HTPB推进剂延伸率二元回归模型[J].
弹箭与制导学报, 2010, 31(4): 261-264. ZOU Si-si, YAN Cong, MA Cen-rui, et al. The dualistic linear regression model of HTPB propellant's elongation under constant strain[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 31(2): 261-264. |
| [17] |
徐进升, 杨晓红, 赵磊, 等. 聚合物时温等效模型有限元应用研究[J].
应用数学和力学, 2015, 36(5): 539-547. XU Jin-sheng, YANG Xiao-hong, ZHAO Lei, et al. Finite element application of the time-temperature superposition principle (TTSP) to polymer[J]. Applied Mathematics and Mechanics, 2015, 36(5): 539-547. DOI:10.3879/j.issn.1000-0887.2015.05.009 |
| [18] |
曹付齐, 刘志成, 李小换. 某固体火箭发动机装药加速老化试验与贮存寿命预测[J].
航空兵器, 2014(4): 59-61. CAO Fu-qi, LIU Zhi-cheng, LI Xiao-huan. Research on accelerated aging test and storage life prediction of solid rocket motor charge[J]. Aero Weaponry, 2014(4): 59-61. |

A one-year accelerated life test was carried out for hydroxyl-terminated polybutadiene(HTPB) propellant under the conditions of 50 ℃, 60 ℃ and 70 ℃, and the maximum elongation was used to characterize the performance of the propellant. According to the characteristics of the aging reaction, a segmented aging model was established. The storage life of HTPB propellant at 25 ℃ is predicted for 11.60 years by using the segmented aging model.



