2. 中国科学院材料力学行为和设计重点实验室, 中国科学技术大学, 安徽 合肥 230026
2. CAS Key Laboratory of Mechanical Behavior and Design of Materials(LMBD), University of Science and Technology of China, Hefei 230026, China
我国露天煤矿的覆盖层硬度普遍比较大, 因此需要通过深孔松动爆破进行剥离。煤矿火区导致的高温炮孔环境可能使爆破器材发生早爆而威胁爆破作业人员的生命安全, 另外高温环境也可能使工业炸药加快热分解而降低炸药性能或者产生拒爆, 从而影响爆破作业整体效果并留下安全隐患[1], 因此迫切需要对高温爆破存在的相关问题进行研究。目前, 研究人员对热作用下的爆破器材性能变化情况进行了广泛研究, 其中傅建秋[2]研究电雷管在高温作用下的性能变化, 结果表明电雷管在温度高于130 ℃时发生自爆; 李战军[3]研究表明2号岩石乳化炸药在80 ℃炮孔中放置数小时后仍能用雷管正常起爆, 在130 ℃的高温作用下经过6 h后失效; 廖明清[4]研究表明受热后的导爆索爆速不变且能起爆防自爆药包。上述研究结论主要是将未防护的爆破器材直接放置在高温炮孔中得出的, 而林谋金[5]提出的全孔蓄水施工方法以及套筒隔热防护都是将爆破器材处于水环境中进行防护, 从而实现工业炸药与起爆器材较长时间保持在安全温度的环境中。水下爆炸测试方法已经广泛应用于工业炸药的做功能力测试, 其通过测定炸药的冲击波能和气泡能而得到做功能力数据, 并与通常评价工业炸药威力的爆力值呈良好的线性关系, 已逐步成为评价炸药做功能力的重要手段, 其做功能力数值通常很接近用爆热弹测量炸药爆轰所释放出的化学能(爆热), 可以用于比较各种炸药的做功能力[6]。目前乳化炸药的爆炸威力在水浴加热后的变化情况在国内外相关文献中公开报道较少, 本研究对乳化炸药采用水浴恒温箱进行水浴加热(以下简称“水浴加热”)来模拟高温炮孔中乳化炸药(水浴防护下)的环境温度, 同时采用水下爆炸实验测定水浴加热前后的乳化炸药爆炸威力的衰减情况,其结果可为煤矿火区高温爆破提供参考。
2 实验部分 2.1 样品制备采用珍珠岩敏化乳胶基质(水含量为12%),其比例为乳胶基质:珍珠岩=96:4,敏化温度为60 ℃, 其中膨胀珍珠岩的粒度90%以上为20~80目, 墩实密度小于0.07 g·mL-1。将乳化炸药用塑料包装成球状药包, 其质量为30 g, 直径约为1.84 cm, 密度为1.13~1.18 g·cm-3。采用水浴恒温箱对药包进行100 ℃水浴加热, 加热时间分别为0, 1, 2, 3, 6 h, 分别得到不同受热时间的样品。
2.2 水下爆炸实验水下爆炸实验采用爆炸罐的直径为D为5 m, 水深H为5 m, 测试装置包括水下压力传感器(PCB, ICPW138A25)、恒流源(482A22)以及泰克示波器(TEKDSO8064A), 如图 1所示。为了满足冲击波和气泡脉动的测试要求, 将药包和传感器置于水面下3 m处, 药包与传感器的距离为120 cm, 每组实验重复3次。
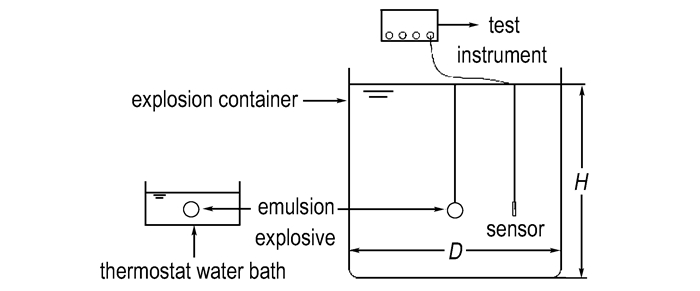
|
图 1 水浴加热与水下爆炸实验示意图 Fig.1 Schematic diagram of underwater explosion experimental system and water-bath heating |
采用图 1所示装置对水浴加热不同时间后的乳化炸药进行水下爆炸爆速实验。爆速实验设备包含有多段智能爆速测量仪2BS-110、空中爆炸容器、细漆包线制成的探针、电线以及Φ32 mm PVC管, 探针间距为4 cm, 炸药质量约为200 g, 测量时将爆速测量仪的时基调至0.1 μs。水浴加热前需要将乳化炸药装入聚氯乙烯(PVC)管后进行密封处理, 防止其在加热过程中膨胀溢出。
3 实验结果与讨论 3.1 冲击波与气泡脉动压力时程曲线水浴加热不同时间的乳化炸药在水下爆炸后产生的典型冲击波压力时程曲线与气泡脉动压力时程曲线如图 2所示,为了便于比较,将图 2中水浴加热不同时间的冲击波压力时程曲线起跳点适当往后调整。

|
图 2 冲击波压力时程曲线与脉动压力时程曲线图 Fig.2 Pressure-time curves for shock wave and bubble pulse |
由图 2可得,乳化炸药的冲击波压力峰值(图 2a)随着水浴加热时间的增加而下降,其原因是乳化炸药水浴加热后出现破乳析晶现象,从而使水浴加热后的乳化炸药的爆炸威力降低。乳化炸药的气泡脉动周期(图 2b)随着水浴加热时间的增加而下降,脉动压力峰值也是随着水浴加热时间的增加而下降。
3.2 水浴加热时间对水下爆炸参数的影响柯克伍德(Kirkwood)和贝蒂(Bethe)通过对压力时程曲线进行积分得到冲击波冲量的计算公式为[7]:
| $ i = \int_0^{6.7\theta } {\Delta p(t){\rm{d}}t} $ | (1) |
式中, i为冲击波冲量,MPa·s; Δp(t)为冲击波压力随时间变化函数,MPa;θ为衰减时间常数,其是压力从峰值pm衰减到pm/e所需的时间,s。G.Bjarnholt得到的水下爆炸参数计算公式为[8-9]:
| $ {E_{\rm{s}}} = 4\pi {R^2}\int_0^{6.7\theta } {\Delta {p^2}(t){\rm{d}}t} /W{\rho _{\rm{w}}}{C_{\rm{w}}} $ | (2) |
| $ {E_{\rm{b}}} = {(\sqrt {1 + 4C{T_{\rm{b}}}}-1)^3}/8{C^3}k_{_1}^{^3}W $ | (3) |
| $ {k_1} = 1.135\rho _{\rm{w}}^{1/2}/P_{\rm{h}}^{5/6} $ | (4) |
| $ {T_{\rm{b}}} = a{W^{1/3}} + b{W^{2/3}} $ | (5) |
| $ C = b/{a^2} $ | (6) |
| $ E = {K_{\rm{f}}}(\mu {E_{\rm{s}}} + {E_{\rm{b}}}) $ | (7) |
| $ \begin{array}{l} \mu = {\rm{ }}1 + 1.3328 \times {10^{-1}}{p_{{\rm{CJ}}}}-6.5775 \times {10^{-3}}p_{{\rm{CJ}}}^2 + \\ 1.2594 \times {10^{ - 4}}p_{{\rm{CJ}}}^3 \end{array} $ | (8) |
| $ {p_{{\rm{CJ}}}} = {\rho _0}{D^2}/4 \times {10^9} $ | (9) |
式中, Es为比冲击波能, MJ·kg-1; R为药包与传感器的距离, m; W为炸药质量, kg; ρw为水的密度, kg·m-3; Cw为水中声速, m·s-1; θ为衰减时间常数, ms; Eb为比气泡能, MJ·kg-1; Tb为气泡第一次脉动周期, s; ph为测点处流体总静水压力, Pa; E为总能量, MJ·kg-1; μ为冲击波能损失系数, 由G.Bjarnholt根据实验值拟合得到; Kf为炸药的形状参数, 对于球形取1.00, 对于非球形取1.02~1.10; ρ0为药包的密度, kg·m-3; D为炸药的爆速, m·s-1; pCJ为C-J压力, GPa。a, b为一定试验条件下的固有常数, 其可根据(Tb, W1/3)数据进行最小二乘法近似拟合计算, C为边界效应的校正系数。实验前取不同质量的乳化炸药(15~50 g)在同等条件下进行实验后拟合得到a=0.239, b=-0.019, C=-0.332 s-1, 拟合过程考虑了起爆雷管的影响, 其拟合相关系数为0.99989, 说明拟合效果较理想。根据上述相应的计算公式对水浴加热不同时间后的乳化炸药水下爆炸参数进行计算, 得到的水下爆炸参数与水浴加热时间的关系如图 3所示。
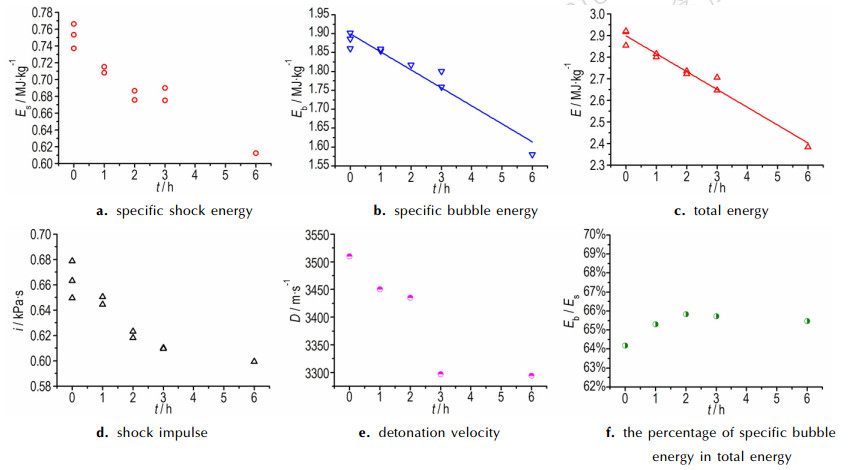
|
图 3 水浴加热对乳化炸药水下爆炸参数的影响 Fig.3 Effect of water-bath heating on the explosion parameter of emulsion explosives |
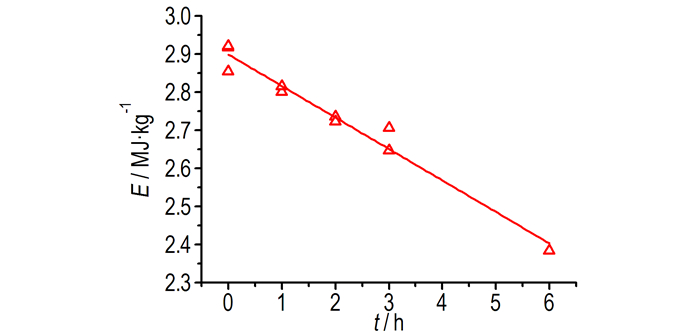
由图 3可得, 乳化炸药的比冲击波能(图 3a)、比气泡能(图 3b)、总能量(图 3c)、冲击波冲量(图 3d)以及爆速(图 3e)随着水浴加热时间的增加而出现下降, 其中乳化炸药的比气泡能与总能量随着水浴加热时间增加呈近似线性降低, 另外乳化炸药比气泡能占总能量的比例(图 3f)随着水浴加热时间增加而变化较小, 其比例保持在65%左右。煤矿火区高温爆破施工中的乳化炸药处于水浴加热时间一般不超过1 h, 因此本文重点关注爆破施工中最不利情况下的爆炸威力衰减情况, 即重点关注乳化炸药在水浴加热1 h后爆炸威力变化。水浴加热1 h后的乳化炸药总能量平均值2.808 MJ·kg-1比未水浴加热的乳化炸药总能量平均值2.901 MJ·kg-1降低了3.17%, 冲击波冲量平均值降低了2.54%, 比冲击波能平均值降低了5.32%, 比气泡能平均值降低了1.33%, 即水浴加热1 h后的乳化炸药爆炸威力下降较小, 同时乳化炸药的油包水结构使大直径药卷内部温度低于水沸点温度, 因此水浴防护后的乳化炸药对煤矿火区爆破效果的影响可以忽略, 即火区爆破的孔网参数设计可以采用常温区爆破的孔网参数。
3.3 能量衰减率计算目前水下爆炸能量的计算公式主要有G.Bjarnholt计算公式[8]与Cole计算公式[10], G.Bjarnholt计算公式计算精度较好而被广泛应用, 但需要另外进行爆速实验得到炸药的爆速参与计算, 而Cole计算公式则不需要另外进行爆速实验且计算过程简单方便, 但需要满足炸药的比气泡能占总能量的比值保持不变的条件。由上文计算结果可知珍珠岩敏化的乳化炸药中比气泡能占总能量的比例(图 3f)在水浴加热前后变化较小, 因此也可采用Cole计算公式快速计算乳化炸药水浴加热后的总能量。根据Cole理论, 炸药在水下爆炸后第一次脉动周期的计算公式为[10-11]:
| $ {T_{\rm{b}}} = K\cdot\rho _{\rm{w}}^{1/2} \cdot {\left( {W \cdot E} \right)^{1/3}}/P_{\rm{h}}^{5/6} $ | (10) |
令β=K·ρw1/2/Ph5/6, 式(10)可变换为:
| $ {T_{\rm{b}}} = \beta \cdot W \cdot {E^{1/3}} $ | (11) |
在特定的实验条件下(水域大小、水深以及炸药类型等保持不变), 可假定β是固定不变, 从而得到水浴加热前后的乳化炸药总能量计算表达式为:
| $ {E_{\rm{t}}} = {T_{{\rm{b}}t}}\beta {^3}/W $ | (12) |
式中, Tbt为水浴加热t小时后第一次脉动周期, s; Et为乳化炸药在水浴加热t小时后的总能量, MJ·kg-1; β值可通过改变特定炸药(未水浴加热)的质量可标定。为了确定实验的β值, 取不同质量的乳化炸药(15~50 g)在同等条件下进行实验, 根据式(11)对进行拟合, 拟合过程也考虑了起爆雷管的影响, 其拟合的结果为β=0.162, 拟合相关系数为0.99996, 拟合效果较理想, 如图 4所示。
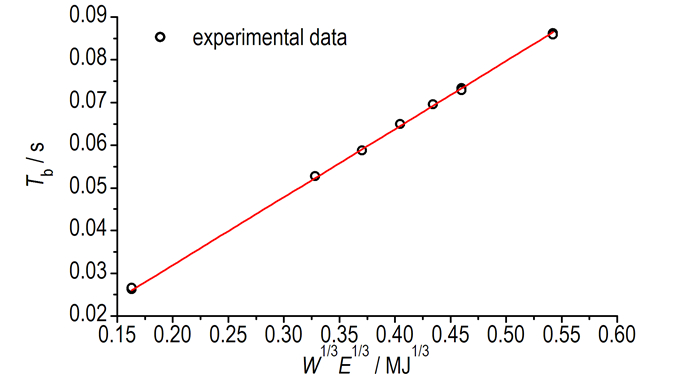
|
图 4 脉动周期线性拟合计算 Fig.4 The linear fit calculation of bubble periods |
将β=0.162代入式(12)后对水浴加热后的乳化炸药总能量进行计算, 并与G.Bjarnholt能量计算结果进行比较, 结果见表 1。为了得到乳化炸药水浴加热后的爆炸能量衰减情况, 将乳化炸药在水浴加热后的能量衰减率定义为η=1-Et/E0, 分别由G.Bjarnholt公式与Cole公式计算得到乳化炸药经过水浴加热不同时间后的能量衰减率见表 1。
| 表 1 Cole与G.Bjarnholt公式计算的总能量 Tab.1 The total energy calculated by formula of Cole and G.Bjarnholt |
由表 1可得, 分别由G.Bjarnholt公式与Cole公式计算得到的能量衰减率都随着水浴加热时间增加呈近似线性增加, 其与乳化炸药的破乳析晶程度随着水浴加热时间增加而加重有关。两种公式计算得到乳化炸药经过水浴加热不同时间后的总能量比较接近, 其最大的相对误差约为6%, 因此采用Cole公式计算乳化炸药水浴加热不同时间后的总能量是可行的。
4 结论(1) 乳化炸药的爆速、冲击波冲量、比冲击波能、比气泡能以及总能量均随着水浴加热时间的增加而出现下降, 其中乳化炸药的比气泡能与总能量随着水浴加热时间增加呈近似线性降低。
(2) 100 ℃水浴加热1 h后的乳化炸药总能量平均值2.808 MJ·kg-1, 比未水浴加热的乳化炸药总能量平均值2.901 MJ·kg-1只降低了3.17%, 另外煤矿火区爆破施工中的乳化炸药处于水浴加热时间一般不超过1 h, 同时乳化炸药的油包水结构使大直径药卷内部温度低于水沸点温度, 因此水浴防护后的乳化炸药对煤矿火区爆破效果的影响可以忽略。
(3) 乳化炸药比气泡能占总能量的比例随着水浴加热时间增加而变化较小, 其满足采用Cole公式计算乳化炸药水浴加热不同时间后总能量的前提条件, 因此也可采用Cole公式计算炸药总能量。
| [1] |
许晨, 李克民, 李晋旭, 等. 露天煤矿高温火区爆破的安全技术探究[J].
露天采矿技术, 2010(4): 73-75. XU Chen, LI Ke-min, LI Jin-xu, et al. Security technology research on high-temperature fire area blasting in surface mine[J]. Opencast Mining Technology, 2010(4): 73-75. |
| [2] |
傅建秋, 李战军, 蔡建德, 等. 胶状乳化炸药和电雷管的耐高温性能试验研究[J].
爆破, 2008, 25(4): 7-10. FU Jian-qiu, LI Zhan-jun, CAI Jian-de, et al. Experimental research on resistance to elevated temperatures of colloidal emulsion explosive and electric detonator[J]. Blasting, 2008, 25(4): 7-10. |
| [3] |
李战军, 郑炳旭. 矿用火工品耐热性现场试验[J].
合肥工业大学学报(自然科学版), 2009, 32(10): 1498-1500. LI Zhan-jun, ZHENG Bing-xu. On-site heat resistant experiments of permissible explosive materials[J]. Journal of Hefei University of Technology(Natural Science), 2009, 32(10): 1498-1500. DOI:10.3969/j.issn.1003-5060.2009.10.011 |
| [4] |
廖明清, 孙孚锜. 普通导爆索在高温爆破中的应用[J].
爆破器材, 1991(1): 19-21. LIAO Ming-qing, SUN Fu-qi. Application of common detonating fuses in high-temperature blasting jobs[J]. Explosive Materials, 1991(1): 19-21. |
| [5] |
林谋金, 郑炳旭, 李战军, 等. 高温炮孔中乳化炸药升温规律分析[J].
爆破器材, 2016, 45(1): 47-50. LIN Mou-jin, ZHENG Bing-xu, LI Zhan-jun, et al. Temperature raising analysis of emulsion explosive in high temperature blast hole[J]. Explosive Materials, 2016, 45(1): 47-50. |
| [6] |
汪旭光.
乳化炸药[M]. 北京: 冶金工业出版社, 2008: 859-864.
WANG Xu-guang. Emulsion explosives[M]. Beijing: Metallurgical Industry Press, 2008: 859-864. |
| [7] |
Kirkwood J G, Bethe H A. The pressure wave produced by an underwater explosion[R]. OSRD Rep, 1942, 588.
|
| [8] |
G.Bjarnholt. Suggestions on standards for measurement and data evaluation in the underwater explosion test[J].
Propellants, Explosives, Pyrotechnics, 1980, 5(2): 67-74. |
| [9] |
林谋金, 马宏昊, 沈兆武, 等. 铝薄膜含量对RDX基铝薄膜炸药水下爆炸威力影响[J].
含能材料, 2014, 22(5): 678-683. LIN Mou-jin, MA Hong-hao, SHEN Zhao-wu, et al. Effect of aluminum film content on underwater explosion performance of RDX-based aluminum film explosive[J]. Chinese Journal of Energetic Materials(Hanneng Cailiao), 2014, 22(5): 678-683. |
| [10] |
Cole R H.
Underwater explosions[M]. New York: Dover Publications, 1965.
|
| [11] |
Willis H F. Underwater explosions: the time interval between successive explosions[J].
British Report, 1941: WA-47-21. |
The enviroment temperature of protected emulsion explosive in high temperature blast hole were simulated by 100 ℃ water bath heating and the underwater explosion parameters were caculated and obtained through underwater explosion experiments.




